Mathematics | Matching (graph theory)
Last Updated :
07 Jan, 2022
Prerequisite – Graph Theory Basics
Given an
undirected graph, a
matching is a set of edges, such that no two edges share the same vertex. In other words, matching of a graph is a subgraph where each node of the subgraph has either
zero or one edge incident to it.
A vertex is said to be
matched if an edge is incident to it,
free otherwise.
Possible matchings of
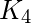
, here the red edges denote the matching –

Matching Terminology –
Maximal Matching – A matching
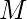
of graph
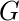
is said to be maximal if on adding an edge which is in
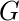
but not in
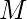
, makes
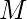
not a matching.
In other words, a maximal matching
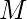
is not a proper subset of any other matching of
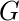
. For example, the following graphs are maximal matchings –

Adding any edge to any of the above graphs would result in them no longer being a matching.
Maximum Matching – A matching
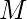
of graph
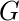
is said to be maximum if it is maximal and has the maximum number of edges.
There may be many possible maximum matchings of a graph.
Every maximum matching is a maximal matching but not every maximal matching is a maximum matching.
For example, in the first figure
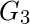
is a maximum matching and in the second figure, the second and third graphs are maximum matchings.
Perfect Matching – A matching
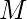
of graph
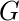
is said to be perfect if
every vertex is connected to exactly one edge. Every perfect matching is a maximum matching but not every maximum matching is a perfect matching.
Since every vertex has to be included in a perfect matching, the number of edges in the matching must be
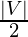
where V is the number of vertices. Therefore, a perfect matching only exists if the number of vertices is even.
For example in the first figure,
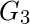
is a perfect matching.
A matching is said to be
near perfect if the number of vertices in the original graph is odd, it is a maximum matching and it leaves out only one vertex. For example in the second figure, the third graph is a near perfect matching.
- Example – Count the number of perfect matchings in a complete graph
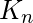 .
.
- Solution – If the number of vertices in the complete graph is odd, i.e.
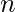 is odd, then the number of perfect matchings is 0.
But if
is odd, then the number of perfect matchings is 0.
But if 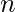 is even then we can derive a general formula for counting the number of perfect matchings.
Since
is even then we can derive a general formula for counting the number of perfect matchings.
Since 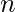 is even, we can denote it as
is even, we can denote it as 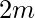 for some positive integer
for some positive integer 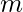 .
Every vertex is connected to every other vertex in a perfect graph, therefore the degree of each vertex is
.
Every vertex is connected to every other vertex in a perfect graph, therefore the degree of each vertex is 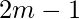 . Out of these
. Out of these 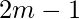 edges we have to choose 1 edge to include two vertices.
We can choose an edge in
edges we have to choose 1 edge to include two vertices.
We can choose an edge in 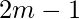 ways. Now
ways. Now 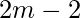 vertices remain and
vertices remain and 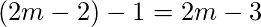 edges remain since the edges connected to the already selected vertices cannot be selected because it is a matching.
So the number of ways of selecting an edge from
edges remain since the edges connected to the already selected vertices cannot be selected because it is a matching.
So the number of ways of selecting an edge from 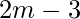 edges is
edges is 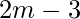 .
We can keep choosing edges in the same way, then by product rule-
Number of perfect matchings-
.
We can keep choosing edges in the same way, then by product rule-
Number of perfect matchings- 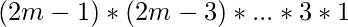 .
This can also be written as-
.
This can also be written as-
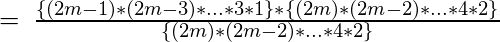
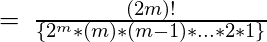
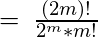 So for a perfect graph with
So for a perfect graph with 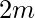 vertices the number of perfect matchings is-
vertices the number of perfect matchings is- 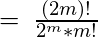
Bipartite Matching –
Matching has many applications in flow networks, scheduling, and planning, graph coloring, neural networks etc. The most common of these is the scheduling problem where there are
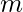
tasks which may be completed by
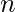
workers. The tasks and workers represent the two sets of vertices in a bipartite graph, where a task is connected to a worker if the worker is able to complete it.
The problem therefore is to find a maximum matching.
More on this topic is discussed in the article –
Maximum Bipartite Matching
GATE CS Corner Questions
Practicing the following questions will help you test your knowledge. All questions have been asked in GATE in previous years or in GATE Mock Tests. It is highly recommended that you practice them.
1.
GATE CS 2003, Question 36
References –
Matching – Wikipedia
Discrete Mathematics and its Applications, by Kenneth H Rosen
Share your thoughts in the comments
Please Login to comment...