Letters for Digits
Last Updated :
18 Mar, 2021
A number multiplied by 2 gives 60. What is that number? The number is 30. That number is not known; assume that number as a variable and what value to be assigned to that variable in order to get the result as 60. Variable is defined as an unknown quantity. No definite value and it keeps changing. It is a puzzle-solving type in which a value for a specified letter needed to be determined. The value of a letter has to have only one digit. If there are multiple letters in a puzzle same values cannot be assigned to multiple letters. The value of a letter cannot be zero if the letter is in the starting position.
Letter for Digits
The problems based on this topic are some puzzles in which letters take the place of digits in an arithmetic addition and the question is to find out which letter represents which digit. Such a kind of puzzling question seems like cracking a code using arithmetic operations.
In this type of puzzles, the letter represents the digits, and one needs to crack the code remembering few things in mind like:
- Each digit in the arithmetic operation represents a single letter and vice-versa.
- Any number used in this, can not have first digit as zero e.g. 25 should not be 025 or 0025.
- And every puzzle must have only one solution or code.
Puzzle with Addition
Consider the following example for a puzzle with addition is given below:
Example: Find the value of unknown Y in the following addition:
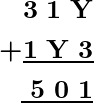
Solution:
It is known that for the given addition there is only one letter Y whose value is needed to determine.
Consider the addition of the first column i.e. from Y + 3 which gives 1 at its one’s place. This implies that Y can be 8 because 8 + 3 = 11 i.e. 1 at one’s place.
If this is so then the given addition must be written as:
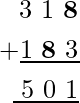
Hence, the value of the unknown Y is 8.
Puzzle with Multiplication
Consider the following example for a puzzle with multiplication is given below:
Example: Determine the values of the unknowns P and Q in the following multiplication.
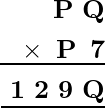
Solution:
Consider the multiplication from the first column i.e. Q × 7 which again gives Q at its one’s place. This implies that Q can be either 0 or 5 because only 0 × 7 = 0 itself and 5 × 7 = 25.
Now, in order to determine the value of P following are the cases:
When P = 1 and Q = 0 then A B × A 7 = 1 0 × 1 7 = 170,
When P = 1 and Q = 5 then A B × A 7 = 1 5 × 1 7 = 255,
When P = 2 and Q = 0 then A B × A 7 = 2 0 × 2 7 = 540,
When P = 2 and Q = 5 then A B × A 7 = 2 5 × 2 7 = 675,
When P = 3 and Q = 0 then A B × A 7 = 3 0 × 3 7 = 1110 and
When P = 3 and Q = 5 then A B × A 7 = 3 0 × 3 7 = 1295.
Hence, the required values of the unknown is: P = 3 and Q = 5.
Sample Problems
Following are some problems based on the above topics:
Problem 1: Find the value of unknowns C and D:
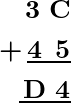
Solution:
Consider the addition of the first column i.e. from C + 5 which gives 4 at its one’s place. This implies that C can be 9 because 9 + 5 = 14 i.e. 1 at one’s place.
If this is so then the given addition must be written as:
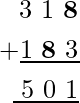
Hence, the value of the unknowns C = 9 & D = 8.
Problem 2: What value for Z is substituted in the following addition to make it true:
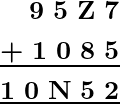
Solution:
Firstly, consider the addition of the first column i.e 7 + 5 = 12 this implies that the addition in second column is: 1 + Z + 8 to give 5 at one’s place. For this case the Z should be 6.
If this is so then the given addition must be written as:
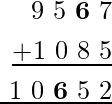
Hence, the value of Z is equal to 6.
Problem 3: What value for P and Q substituted in the following multiplication problem to make it true:
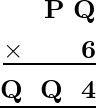
Solution:
For the given case the product of Q and 6 must be same as ones place digit i.e Q.
Now,
1 × 6 = 6,
2 × 6 = 12,
3 × 6 = 18,
4 × 6 = 24
Thus, one of the digit multiplied and the ones place digit of the product obtained is same.
So, the given multiplication becomes:
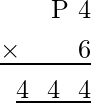
Now, the value of P is obtained as:
On putting Q = 4, the ones digit must be obtained as 4 and the remaining two values of Q should be 44, which can be possible when 7 is multiplied with 6 to give 44. Therefore, the given multiplication becomes:
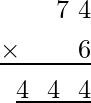
Hence, the value of P and Q are 7 and 4.
Problem 4: What value for X and Y substituted in the following addition problem to make it true:
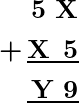
Solution:
Consider the first column of the addition i.e. the sum of X and 5 gives 9 at one’s place, this can be possible when 4 is added to 5.
Therefore, the given addition problem becomes:
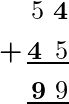
Hence, the value of X and Y are 4 and 9.
Problem 5: What is the value of A – B when A 3 + 8 B = 150.
Solution:
Consider the addition of one’s place digits first i.e. the sum of 3 and B is such that the digit at one’s place is 0.
This is possible when B is 7 i.e. 3 + 7 = 10. So the given addition becomes: 6 3 + 8 7 = 150.
This implies that A = 6 and B = 7.
Thus, A – B = 6 – 7 = -1.
Share your thoughts in the comments
Please Login to comment...