Introduction to Convolution Neural Network
Last Updated :
14 Mar, 2024
A Convolutional Neural Network (CNN) is a type of Deep Learning neural network architecture commonly used in Computer Vision. Computer vision is a field of Artificial Intelligence that enables a computer to understand and interpret the image or visual data.
When it comes to Machine Learning, Artificial Neural Networks perform really well. Neural Networks are used in various datasets like images, audio, and text. Different types of Neural Networks are used for different purposes, for example for predicting the sequence of words we use Recurrent Neural Networks more precisely an LSTM, similarly for image classification we use Convolution Neural networks. In this blog, we are going to build a basic building block for CNN.
In a regular Neural Network there are three types of layers:
- Input Layers: It’s the layer in which we give input to our model. The number of neurons in this layer is equal to the total number of features in our data (number of pixels in the case of an image).
- Hidden Layer: The input from the Input layer is then fed into the hidden layer. There can be many hidden layers depending on our model and data size. Each hidden layer can have different numbers of neurons which are generally greater than the number of features. The output from each layer is computed by matrix multiplication of the output of the previous layer with learnable weights of that layer and then by the addition of learnable biases followed by activation function which makes the network nonlinear.
- Output Layer: The output from the hidden layer is then fed into a logistic function like sigmoid or softmax which converts the output of each class into the probability score of each class.
The data is fed into the model and output from each layer is obtained from the above step is called feedforward, we then calculate the error using an error function, some common error functions are cross-entropy, square loss error, etc. The error function measures how well the network is performing. After that, we backpropagate into the model by calculating the derivatives. This step is called Backpropagation which basically is used to minimize the loss.
Convolution Neural Network
Convolutional Neural Network (CNN) is the extended version of artificial neural networks (ANN) which is predominantly used to extract the feature from the grid-like matrix dataset. For example visual datasets like images or videos where data patterns play an extensive role.
CNN architecture
Convolutional Neural Network consists of multiple layers like the input layer, Convolutional layer, Pooling layer, and fully connected layers.
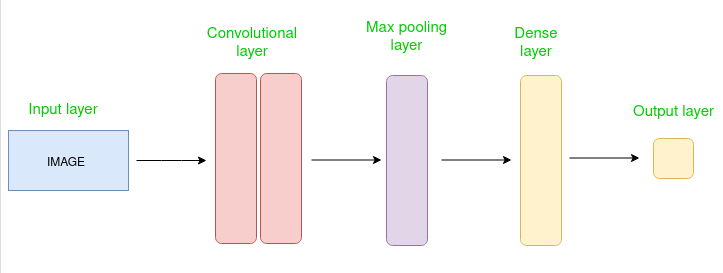
Simple CNN architecture
The Convolutional layer applies filters to the input image to extract features, the Pooling layer downsamples the image to reduce computation, and the fully connected layer makes the final prediction. The network learns the optimal filters through backpropagation and gradient descent.
How Convolutional Layers works
Convolution Neural Networks or covnets are neural networks that share their parameters. Imagine you have an image. It can be represented as a cuboid having its length, width (dimension of the image), and height (i.e the channel as images generally have red, green, and blue channels).

Now imagine taking a small patch of this image and running a small neural network, called a filter or kernel on it, with say, K outputs and representing them vertically. Now slide that neural network across the whole image, as a result, we will get another image with different widths, heights, and depths. Instead of just R, G, and B channels now we have more channels but lesser width and height. This operation is called Convolution. If the patch size is the same as that of the image it will be a regular neural network. Because of this small patch, we have fewer weights.

Image source: Deep Learning Udacity
Now let’s talk about a bit of mathematics that is involved in the whole convolution process.
- Convolution layers consist of a set of learnable filters (or kernels) having small widths and heights and the same depth as that of input volume (3 if the input layer is image input).
- For example, if we have to run convolution on an image with dimensions 34x34x3. The possible size of filters can be axax3, where ‘a’ can be anything like 3, 5, or 7 but smaller as compared to the image dimension.
- During the forward pass, we slide each filter across the whole input volume step by step where each step is called stride (which can have a value of 2, 3, or even 4 for high-dimensional images) and compute the dot product between the kernel weights and patch from input volume.
- As we slide our filters we’ll get a 2-D output for each filter and we’ll stack them together as a result, we’ll get output volume having a depth equal to the number of filters. The network will learn all the filters.
Layers used to build ConvNets
A complete Convolution Neural Networks architecture is also known as covnets. A covnets is a sequence of layers, and every layer transforms one volume to another through a differentiable function.
Types of layers: datasets
Let’s take an example by running a covnets on of image of dimension 32 x 32 x 3.
- Input Layers: It’s the layer in which we give input to our model. In CNN, Generally, the input will be an image or a sequence of images. This layer holds the raw input of the image with width 32, height 32, and depth 3.
- Convolutional Layers: This is the layer, which is used to extract the feature from the input dataset. It applies a set of learnable filters known as the kernels to the input images. The filters/kernels are smaller matrices usually 2×2, 3×3, or 5×5 shape. it slides over the input image data and computes the dot product between kernel weight and the corresponding input image patch. The output of this layer is referred as feature maps. Suppose we use a total of 12 filters for this layer we’ll get an output volume of dimension 32 x 32 x 12.
- Activation Layer: By adding an activation function to the output of the preceding layer, activation layers add nonlinearity to the network. it will apply an element-wise activation function to the output of the convolution layer. Some common activation functions are RELU: max(0, x), Tanh, Leaky RELU, etc. The volume remains unchanged hence output volume will have dimensions 32 x 32 x 12.
- Pooling layer: This layer is periodically inserted in the covnets and its main function is to reduce the size of volume which makes the computation fast reduces memory and also prevents overfitting. Two common types of pooling layers are max pooling and average pooling. If we use a max pool with 2 x 2 filters and stride 2, the resultant volume will be of dimension 16x16x12.

Image source: cs231n.stanford.edu
- Flattening: The resulting feature maps are flattened into a one-dimensional vector after the convolution and pooling layers so they can be passed into a completely linked layer for categorization or regression.
- Fully Connected Layers: It takes the input from the previous layer and computes the final classification or regression task.

Image source: cs231n.stanford.edu
- Output Layer: The output from the fully connected layers is then fed into a logistic function for classification tasks like sigmoid or softmax which converts the output of each class into the probability score of each class.
Example:
Let’s consider an image and apply the convolution layer, activation layer, and pooling layer operation to extract the inside feature.
Input image:

Input image
Step:
- import the necessary libraries
- set the parameter
- define the kernel
- Load the image and plot it.
- Reformat the image
- Apply convolution layer operation and plot the output image.
- Apply activation layer operation and plot the output image.
- Apply pooling layer operation and plot the output image.
Python3
import numpy as np
import tensorflow as tf
import matplotlib.pyplot as plt
from itertools import product
plt.rc('figure', autolayout=True)
plt.rc('image', cmap='magma')
kernel = tf.constant([[-1, -1, -1],
[-1, 8, -1],
[-1, -1, -1],
])
image = tf.io.read_file('Ganesh.jpg')
image = tf.io.decode_jpeg(image, channels=1)
image = tf.image.resize(image, size=[300, 300])
img = tf.squeeze(image).numpy()
plt.figure(figsize=(5, 5))
plt.imshow(img, cmap='gray')
plt.axis('off')
plt.title('Original Gray Scale image')
plt.show();
image = tf.image.convert_image_dtype(image, dtype=tf.float32)
image = tf.expand_dims(image, axis=0)
kernel = tf.reshape(kernel, [*kernel.shape, 1, 1])
kernel = tf.cast(kernel, dtype=tf.float32)
conv_fn = tf.nn.conv2d
image_filter = conv_fn(
input=image,
filters=kernel,
strides=1,
padding='SAME',
)
plt.figure(figsize=(15, 5))
plt.subplot(1, 3, 1)
plt.imshow(
tf.squeeze(image_filter)
)
plt.axis('off')
plt.title('Convolution')
relu_fn = tf.nn.relu
image_detect = relu_fn(image_filter)
plt.subplot(1, 3, 2)
plt.imshow(
tf.squeeze(image_detect)
)
plt.axis('off')
plt.title('Activation')
pool = tf.nn.pool
image_condense = pool(input=image_detect,
window_shape=(2, 2),
pooling_type='MAX',
strides=(2, 2),
padding='SAME',
)
plt.subplot(1, 3, 3)
plt.imshow(tf.squeeze(image_condense))
plt.axis('off')
plt.title('Pooling')
plt.show()
|
Output:
.png)
Original Grayscale image
.jpg)
Output
Advantages of Convolutional Neural Networks (CNNs):
- Good at detecting patterns and features in images, videos, and audio signals.
- Robust to translation, rotation, and scaling invariance.
- End-to-end training, no need for manual feature extraction.
- Can handle large amounts of data and achieve high accuracy.
Disadvantages of Convolutional Neural Networks (CNNs):
- Computationally expensive to train and require a lot of memory.
- Can be prone to overfitting if not enough data or proper regularization is used.
- Requires large amounts of labeled data.
- Interpretability is limited, it’s hard to understand what the network has learned.
Frequently Asked Questions (FAQs)
1: What is a Convolutional Neural Network (CNN)?
A Convolutional Neural Network (CNN) is a type of deep learning neural network that is well-suited for image and video analysis. CNNs use a series of convolution and pooling layers to extract features from images and videos, and then use these features to classify or detect objects or scenes.
2: How do CNNs work?
CNNs work by applying a series of convolution and pooling layers to an input image or video. Convolution layers extract features from the input by sliding a small filter, or kernel, over the image or video and computing the dot product between the filter and the input. Pooling layers then downsample the output of the convolution layers to reduce the dimensionality of the data and make it more computationally efficient.
3: What are some common activation functions used in CNNs?
Some common activation functions used in CNNs include:
- Rectified Linear Unit (ReLU): ReLU is a non-saturating activation function that is computationally efficient and easy to train.
- Leaky Rectified Linear Unit (Leaky ReLU): Leaky ReLU is a variant of ReLU that allows a small amount of negative gradient to flow through the network. This can help to prevent the network from dying during training.
- Parametric Rectified Linear Unit (PReLU): PReLU is a generalization of Leaky ReLU that allows the slope of the negative gradient to be learned.
4: What is the purpose of using multiple convolution layers in a CNN?
Using multiple convolution layers in a CNN allows the network to learn increasingly complex features from the input image or video. The first convolution layers learn simple features, such as edges and corners. The deeper convolution layers learn more complex features, such as shapes and objects.
5: What are some common regularization techniques used in CNNs?
Regularization techniques are used to prevent CNNs from overfitting the training data. Some common regularization techniques used in CNNs include:
- Dropout: Dropout randomly drops out neurons from the network during training. This forces the network to learn more robust features that are not dependent on any single neuron.
- L1 regularization: L1 regularization regularizes the absolute value of the weights in the network. This can help to reduce the number of weights and make the network more efficient.
- L2 regularization: L2 regularization regularizes the square of the weights in the network. This can also help to reduce the number of weights and make the network more efficient.
6: What is the difference between a convolution layer and a pooling layer?
A convolution layer extracts features from an input image or video, while a pooling layer downsamples the output of the convolution layers. Convolution layers use a series of filters to extract features, while pooling layers use a variety of techniques to downsample the data, such as max pooling and average pooling.
Share your thoughts in the comments
Please Login to comment...