Learn Algorithms with Javascript | DSA using JavaScript Tutorial

This Algorithms with Javascript tutorial is designed to help you understand and implement fundamental algorithms using the versatile JavaScript programming language. Whether you are a beginner in programming or looking to enhance your algorithmic skills, this guide will walk you through essential concepts, algorithms, and their implementations.

What is an Algorithm?

The algorithm is defined as a process or set of well-defined instructions that are typically used to solve a particular set of problems or perform a specific type of calculation. To explain it in simpler terms, it is a set of operations performed step-by-step to execute a task.

How to Start learning Algorithms in JavaScript?

Follow the below mentioned points for how to learn Algorithms in JavaScript:

• Know the fundamentals of Algorithms inside and out.
• Know exactly what happens in an algorithm.
• Understand the examples and grasp the algorithm’s steps.
• Clearly know complexity analysis of algorithms in best, average and worst case.
• Solve problems based on the algorithms on your own.

Must know Algorithms in DSA using JavaScript Tutorial

The algorithms are divided into several categories, as shown below:

1. Searching Algorithms in Javascript:

Searching algorithms are used to find a specific element in an array, string, linked list, or some other data structure. 

The most common search algorithms are:

1.1 Linear Search Algorithm in Javascript

In the Linear searching algorithm, we check for the element iteratively one by one from start to end to the other.

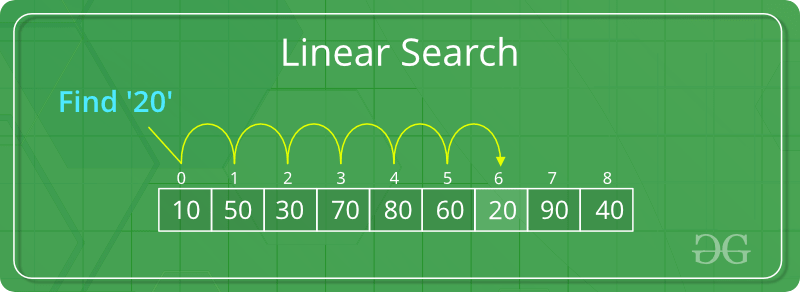
Linear search

How Linear Search Works?

• Step 1: First, read the array’s search element (Target element).
• Step 2: Set an integer i = 0 and repeat steps 3 to 4 until i reaches the array’s end.
• Step 3: Match the key with arr[i].
• Step 4: If the key matches, return the index. Otherwise, increment i by 1.

Below is the implementation of Linear Search in javascript:

Javascript

// Javascript code to linearly search x in arr[].

// If x is present then return its location,
// otherwise return -1
function linearSearch(arr, n, x) {
    let i;
    for (i = 0; i < n; i++)
        if (arr[i] == x)
            return i;
    return -1;
}

// Function to call Linear Search method
function searchInArr(arr, n, x) {

    // Function call
    let result = linearSearch(arr, n, x);
    if (result == -1)
        console.log("Element is not present in array");
    else
        console.log("Element is present at index " + result);
}

// Driver code

let arr = [10, 30, 50, 60, 70];
let n = arr.length;

let x1 = 50;
searchInArr(arr, n, x1);

let x2 = 5;
searchInArr(arr, n, x2);

Output

Element is present at index 2
Element is not present in array

Complexity Analysis of Linear Search Algorithm

• Time Complexity of Linear Search: O(N), where N is the number of elements in the Array
• Auxiliary Space Complexity of Linear Search: O(1)

1.2) Binary Search Algorithm in Javascript

• In this type of searching algorithm, we break the data structure into two equal parts and try to decide in which half we need to find the element target element. 

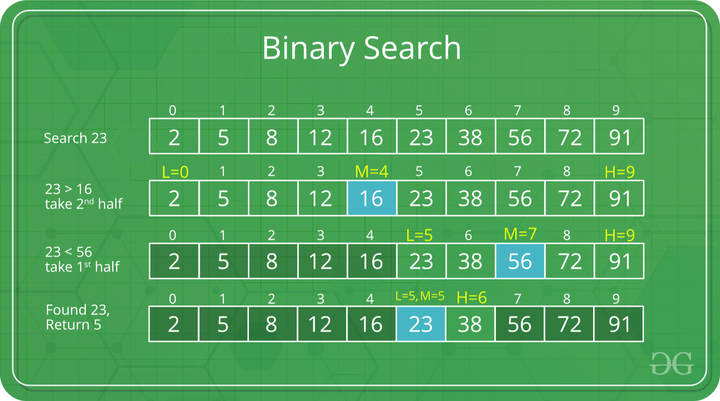
Binary Search

How does Binary Search work?

To understand the working of binary search, consider the following illustration:

• First Step:
  • Initially, the search space is from 0 to 9. 
  • Let’s denote the boundary by L and H where L = 0 and H = 9 initially. 
  • Now mid of this search space is M = 4. 
  • So compare the target with arr[M].
• Second Step:
  • As arr[4] is less than the target, switch the search space to the right of 16, i.e., [5, 9]. 
  • Now L = 5, H = 9, and M becomes 7. 
  • Compare target with arr[M].
• Third Step:
  • arr[7] is greater than the target. 
  • Shift the search space to the left of M, i.e., [5, 6]. 
  • So, now L = 5, H = 6 and M = 6. 
  • Compare arr[M] with the target. 
  • Here arr[M] and target are the same. 
• So, we have found the target.

Here is the implementation of the above approach:

Javascript

// Iterative function to implement Binary Search
let iterativeFunction = function (arr, x) {

    let start=0, end=arr.length-1;

    // Iterate while start not meets end
    while (start<=end){

        // Find the mid index
        let mid=Math.floor((start + end)/2);

        // If element is present at mid, return True
        if (arr[mid]===x) return true;

        // Else look in left or right half accordingly
        else if (arr[mid] < x)
            start = mid + 1;
        else
            end = mid - 1;
    }

    return false;
}

// Driver code
let arr = [1, 3, 5, 7, 8, 9];
let x = 5;

if (iterativeFunction(arr, x, 0, arr.length-1))
    console.log("Element found!");
else console.log("Element not found!");

x = 6;

if (iterativeFunction(arr, x, 0, arr.length-1))
    console.log("Element found!");
else console.log("Element not found!");

Output

Element found!
Element not found!

Time Complexity: O(logN)
Auxiliary Space: O(1) 

2. Sorting Algorithm in javascript:

A Sorting Algorithm is used to arrange a given array or list of elements according to a comparison operator on the elements. The comparison operator is used to decide the new order of elements in the respective data structure.

The most common sorting algorithms are:

• Bubble sort
• Insertion sort
• Selection sort
• Quick sort
• Merge sort

2.1)Bubble sort  in Javascript:

Bubble sort

Below is the implementation of bubble sort in javascript:

Javascript

function swap(arr, xp, yp)
{
    var temp = arr[xp];
    arr[xp] = arr[yp];
    arr[yp] = temp;
}

// An optimized version of Bubble Sort
function bubbleSort( arr, n)
{
var i, j;
for (i = 0; i < n-1; i++)
{
    for (j = 0; j < n-i-1; j++)
    {
        if (arr[j] > arr[j+1])
        {
        swap(arr,j,j+1);

        }
    }

}
}

/* Function to print an array */
function printArray(arr, size)
{
    var i;
    for (i=0; i < size; i++)
        console.log(arr[i]+ " ");

}

// Driver program to test above functions
var arr = [5, 1, 4, 2, 8];
    var n = 5;
    console.log("UnSorted array:");
    printArray(arr, n);

    bubbleSort(arr, n);
    console.log("Sorted array: ");
    printArray(arr, n);

Output

UnSorted array:
5 
1 
4 
2 
8 
Sorted array: 
1 
2 
4 
5 
8 

2.2)Insertion Sort  in Javascript:

Insertion sort

Below is the implementation of Insertion sort in javascript:

Javascript

// Javascript program for insertion sort

// Function to sort an array using insertion sort
function insertionSort(arr, n)
{
    let i, key, j;
    for (i = 1; i < n; i++)
    {
        key = arr[i];
        j = i - 1;

        /* Move elements of arr[0..i-1], that are
        greater than key, to one position ahead
        of their current position */
        while (j >= 0 && arr[j] > key)
        {
            arr[j + 1] = arr[j];
            j = j - 1;
        }
        arr[j + 1] = key;
    }
}

// A utility function to print an array of size n
function printArray(arr, n)
{
    let i;
    for (i = 0; i < n; i++)
        console.log(arr[i] + " ");

}

// Driver code
    let arr = [12, 11, 13, 5, 6 ];
    let n = arr.length;
    console.log("Elements before sorting:")
    printArray(arr, n);
    insertionSort(arr, n);
    console.log("Elements after sorting:")
    printArray(arr, n);

Output

Elements before sorting:
12 
11 
13 
5 
6 
Elements after sorting:
5 
6 
11 
12 
13 

2.3)Selection sort in Javascript:

Selection sort

Below is the implementation of selection sort in javascript:

Javascript

// Javascript program for implementation of selection sort
function swap(arr,xp, yp)
{
    var temp = arr[xp];
    arr[xp] = arr[yp];
    arr[yp] = temp;
}

function selectionSort(arr, n)
{
    var i, j, min_idx;

    // One by one move boundary of unsorted subarray
    for (i = 0; i < n-1; i++)
    {
        // Find the minimum element in unsorted array
        min_idx = i;
        for (j = i + 1; j < n; j++)
        if (arr[j] < arr[min_idx])
            min_idx = j;

        // Swap the found minimum element with the first element
        swap(arr,min_idx, i);
    }
}

function printArray( arr, size)
{
    var i;
    for (i = 0; i < size; i++)
        console.log(arr[i] + " ");
}

var arr = [64, 25, 12, 22, 11];
var n = 5;
console.log("UnSorted array: ");
printArray(arr, n);
selectionSort(arr, n);
console.log("Sorted array:");
printArray(arr, n);

Output

UnSorted array: 
64 
25 
12 
22 
11 
Sorted array:
11 
12 
22 
25 
64 

3. Recursive Algorithm in javascript:

The process in which a function calls itself directly or indirectly is called recursion and the corresponding function is called a recursive function. Using a recursive algorithm, certain problems can be solved quite easily. Examples of such problems are Towers of Hanoi (TOH), Inorder/Preorder/Postorder Tree Traversals, DFS of Graph, etc

3.1) Tower of Hanoi in javascript:

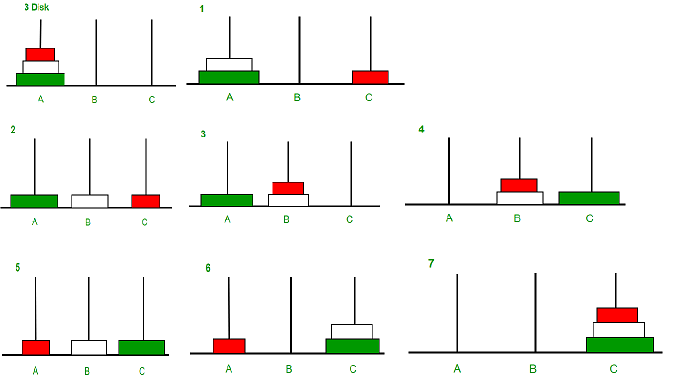
Tower of Hanoi

Below is the implementation of Tower of Hanoi in javascript:

Javascript

// javascript recursive function to
// solve tower of hanoi puzzle
function towerOfHanoi(n, from_rod, to_rod, aux_rod)
{
        if (n == 0)
        {
            return;
        }
        towerOfHanoi(n - 1, from_rod, aux_rod, to_rod);
        console.log("Move disk " + n + " from rod " + from_rod +
        " to rod " + to_rod);
        towerOfHanoi(n - 1, aux_rod, to_rod, from_rod);
    }

    // Driver code
    var N = 3;

    // A, B and C are names of rods
    towerOfHanoi(N, 'A', 'C', 'B');

// This code is contributed by gauravrajput1

Output

Move disk 1 from rod A to rod C
Move disk 2 from rod A to rod B
Move disk 1 from rod C to rod B
Move disk 3 from rod A to rod C
Move disk 1 from rod B to rod A
Move disk 2 from rod B to rod C
Move disk 1 from rod A to rod C

3.2)DFS of a Graph in javascript:

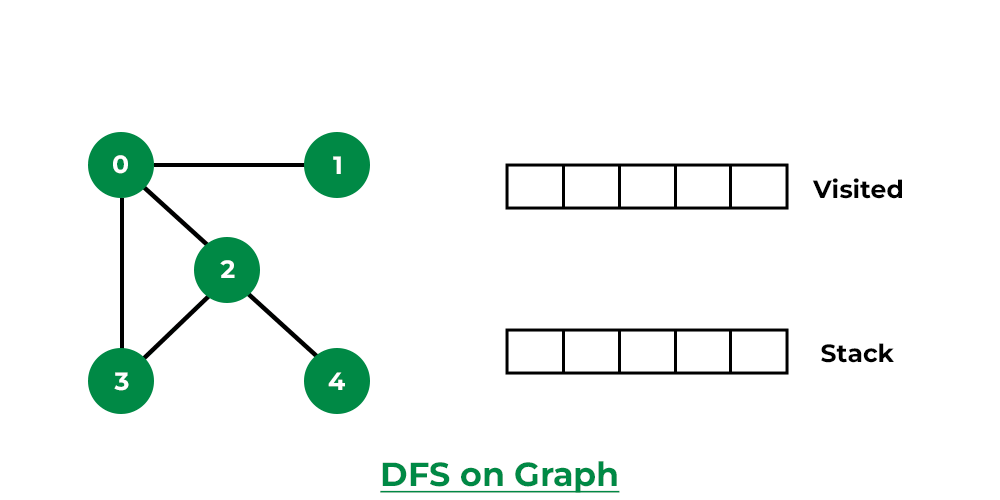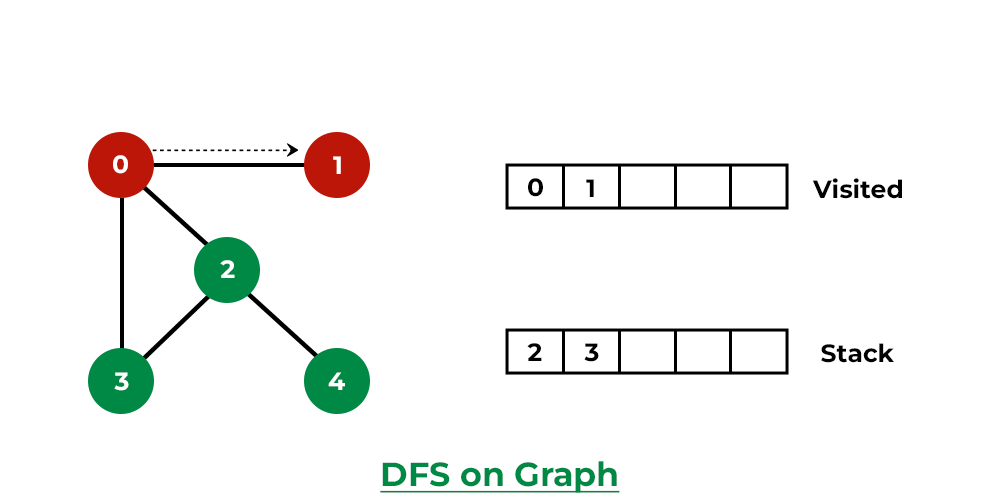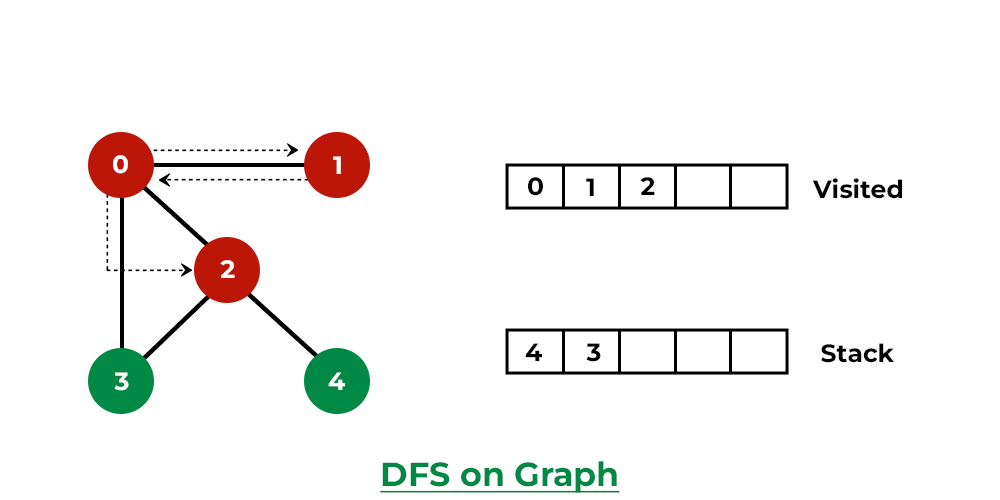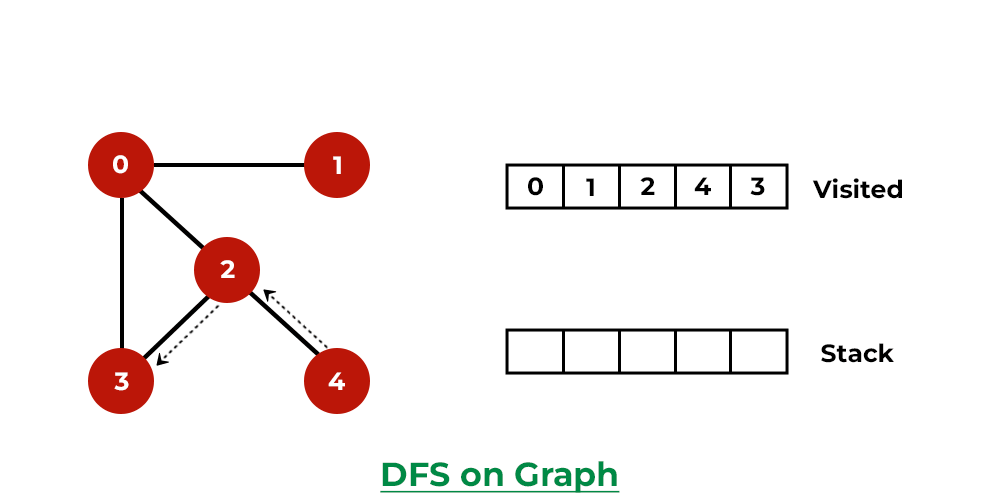
DFS of a Graph

Below is the implementation of DFS in javascript:

Javascript

// JavaScript program to print DFS
    // traversal from a given
    // graph

    // This class represents a
    // directed graph using adjacency
    // list representation
    class Graph
    {

        // Constructor
        constructor(v) {
        this.V = v;
        this.adj = new Array(v).fill([]);
        }

        // Function to Add an edge into the graph
        AddEdge(v, w) {
        this.adj[v].push(w); // Add w to v's list.
        }

        // A function used by DFS
        DFSUtil(v, visited)
        {

        // Mark the current
        // node as visited and print it
        visited[v] = true;
        console.log(v + " ");

        // Recur for all the
        // vertices adjacent to this
        // vertex
        for (const n of this.adj[v]) {
            if (!visited[n]) this.DFSUtil(n, visited);
        }
        }

        // The function to do
        // DFS traversal. It uses recursive
        // DFSUtil()
        DFS()
        {

        // Mark all the vertices as not visited(set as
        var visited = new Array(this.V).fill(false);

        // Call the recursive helper
        // function to print DFS
        // traversal starting from
        // all vertices one by one
        for (var i = 0; i < this.V; ++i)
            if (visited[i] == false) this.DFSUtil(i, visited);
        }
    }

    // Driver Code
    var g = new Graph(4);

    g.AddEdge(0, 1);
    g.AddEdge(0, 2);
    g.AddEdge(1, 2);
    g.AddEdge(2, 0);
    g.AddEdge(2, 3);
    g.AddEdge(3, 3);

    console.log("Following is Depth First Traversal<br>");

    g.DFS();

    // This code is contributed by rdtank.

Output

Following is Depth First Traversal<br>
0 
1 
2 
3 

3.3)Fibonacci algorithm in javascript:

Fibonacci number

Below is the implementation of the Fibonacci number in javascript:

Javascript

//Fibonacci Series using Recursion
    let n = 9;

    // function returns the Fibonacci number
    function fib(n) {
    if (n <= 1)
        return n;
    return fib(n-1) + fib(n-2);
}

    //function call
    console.log(fib(n));
//This code is contributed by Surbhi Tyagi

Output

34

4. Backtracking Algorithm in javascript:

Backtracking can be defined as a general algorithmic technique that considers searching every possible combination in order to solve a computational problem

4.1) Sudoku algorithm in javascript:

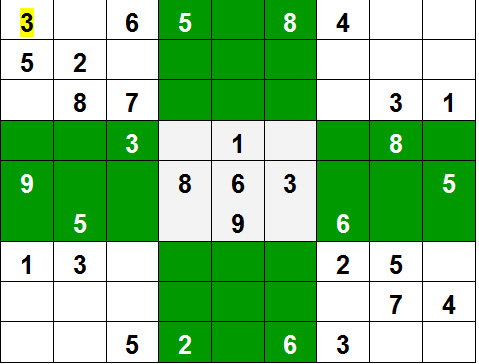
Sudoku Algorithm

Below is the implementation of the sudoku algorithm in javascript:

Javascript

// Javascript program for above approach

// N is the size of the 2D matrix N*N
let N = 9;

/* Takes a partially filled-in grid and attempts
    to assign values to all unassigned locations in
    such a way to meet the requirements for
    Sudoku solution (non-duplication across rows,
    columns, and boxes) */
function solveSudoku(grid, row, col)
{

    /* If we have reached the 8th
    row and 9th column (0
    indexed matrix) ,
    we are returning true to avoid further
    backtracking     */
    if (row == N - 1 && col == N)
        return true;

    // Check if column value becomes 9 ,
    // we move to next row
    // and column start from 0
    if (col == N)
    {
        row++;
        col = 0;
    }

    // Check if the current position
    // of the grid already
    // contains value >0, we iterate
    // for next column
    if (grid[row][col] != 0)
        return solveSudoku(grid, row, col + 1);

    for(let num = 1; num < 10; num++)
    {

        // Check if it is safe to place
        // the num (1-9) in the given
        // row ,col ->we move to next column
        if (isSafe(grid, row, col, num))
        {

            /* assigning the num in the current
            (row,col) position of the grid and
            assuming our assigned num in the position
            is correct */
            grid[row][col] = num;

            // Checking for next
            // possibility with next column
            if (solveSudoku(grid, row, col + 1))
                return true;
        }

        /* removing the assigned num , since our
        assumption was wrong , and we go for next
        assumption with diff num value */
        grid[row][col] = 0;
    }
    return false;
}

/* A utility function to print grid */

// Check whether it will be legal
// to assign num to the
// given row, col
function isSafe(grid, row, col, num)
{

    // Check if we find the same num
    // in the similar row , we
    // return false
    for(let x = 0; x <= 8; x++)
        if (grid[row][x] == num)
            return false;

    // Check if we find the same num
    // in the similar column ,
    // we return false
    for(let x = 0; x <= 8; x++)
        if (grid[x][col] == num)
            return false;

    // Check if we find the same num
    // in the particular 3*3
    // matrix, we return false
    let startRow = row - row % 3,
        startCol = col - col % 3;

    for(let i = 0; i < 3; i++)
        for(let j = 0; j < 3; j++)
            if (grid[i + startRow][j + startCol] == num)
                return false;

    return true;
}

// Driver Code
let grid = [ [ 3, 0, 6, 5, 0, 8, 4, 0, 0 ],
            [ 5, 2, 0, 0, 0, 0, 0, 0, 0 ],
            [ 0, 8, 7, 0, 0, 0, 0, 3, 1 ],
            [ 0, 0, 3, 0, 1, 0, 0, 8, 0 ],
            [ 9, 0, 0, 8, 6, 3, 0, 0, 5 ],
            [ 0, 5, 0, 0, 9, 0, 6, 0, 0 ],
            [ 1, 3, 0, 0, 0, 0, 2, 5, 0 ],
            [ 0, 0, 0, 0, 0, 0, 0, 7, 4 ],
            [ 0, 0, 5, 2, 0, 6, 3, 0, 0 ] ];

if (solveSudoku(grid, 0, 0))
    console.log(grid);
else
    console.log("no solution exists ");

// This code is contributed by rag2127

Output

[
  [
    3, 1, 6, 5, 7,
    8, 4, 9, 2
  ],
  [
    5, 2, 9, 1, 3,
    4, 7, 6, 8
  ],
  [
    4, 8, 7, 6, 2,
    9, 5, 3, 1
  ],
  [
    2, 6, 3, 4, 1,
    5, 9, 8, 7
  ],
  [
    9, 7, 4, 8, 6,
    3, 1, 2, 5
  ],
  [
    8, 5, 1, 7, 9,
    2, 6, 4, 3
  ],
  [
    1, 3, 8, 9, 4,
    7, 2, 5, 6
  ],
  [
    6, 9, 2, 3, 5,
    1, 8, 7, 4
  ],
  [
    7, 4, 5, 2, 8,
    6, 3, 1, 9
  ]
]

4.2) m Coloring Problem in javascript:

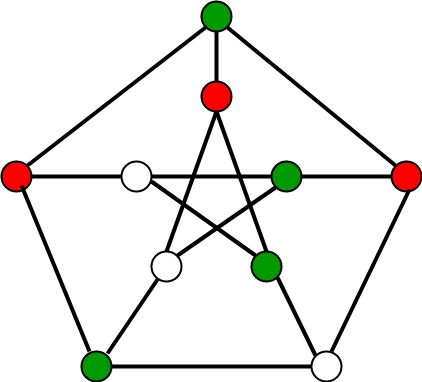
M Coloring Problem

Below is the implementation of the M-coloring Problem in javascript:

Javascript

// Number of vertices in the graph
    let V = 4;

    /* A utility function to print solution */
    function printSolution(color)
    {
        console.log("Solution Exists:" +
    " Following are the assigned colors ");
        for (let i = 0; i < V; i++)
            console.log("  " + color[i]);
        console.log(" ");
    }

    // check if the colored
// graph is safe or not
    function isSafe(graph,color)
    {
        // check for every edge
    for (let i = 0; i < V; i++)
    for (let j = i + 1; j < V; j++)
        if (graph[i][j] && color[j] == color[i])
        return false;
    return true;
    }


/* This function solves the m Coloring
    problem using recursion. It returns
    false if the m colours cannot be assigned,
    otherwise, return true and prints
    assignments of colours to all vertices.
    Please note that there may be more than
    one solutions, this function prints one
    of the feasible solutions.*/
    function graphColoring(graph,m,i,color)
    {
        // if current index reached end
    if (i == V) {

    // if coloring is safe
    if (isSafe(graph, color))
    {

        // Print the solution
        printSolution(color);
        return true;
    }
    return false;
    }

    // Assign each color from 1 to m
    for (let j = 1; j <= m; j++)
    {
    color[i] = j;

    // Recur of the rest vertices
    if (graphColoring(graph, m, i + 1, color))
        return true;
    color[i] = 0;
    }
    return false;
    }

    // Driver code

    /* Create following graph and
        test whether it is 3 colorable
        (3)---(2)
        | / |
        | / |
        | / |
        (0)---(1)
        */
    let graph=[[ false, true, true, true],
            [ true, false, true, false ],
            [ true, true, false, true ],
            [true, false, true, false]];

    let m = 3; // Number of colors

    // Initialize all color values as 0.
    // This initialization is needed
    // correct functioning of isSafe()
    let color = new Array(V);
    for (let i = 0; i < V; i++)
    color[i] = 0;

    if (!graphColoring(graph, m, 0, color))
    console.log("Solution does not exist");


    // This code is contributed by unknown2108

Output

Solution Exists: Following are the assigned colors 
  1
  2
  3
  2
 

4.3) N Queen Problem in  javascript:

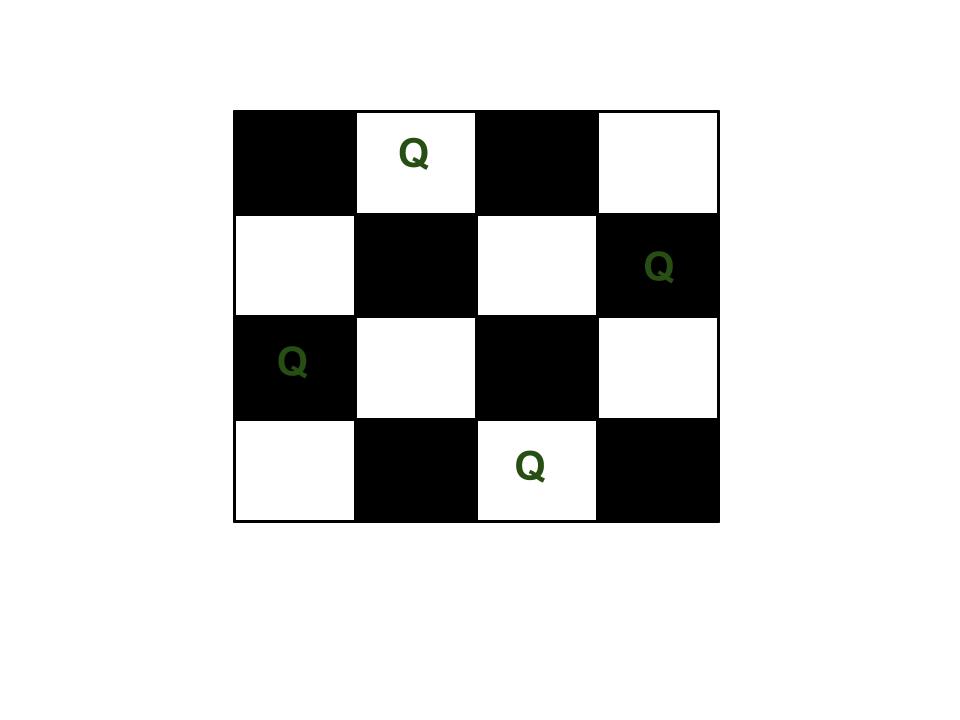
N Queen Problem

Below is the implementation of the N-Queen Problem in javascript:

Javascript

// JavaScript program to solve N Queen
// Problem using backtracking
const N = 4

function printSolution(board)
{
    for(let i = 0; i < N; i++)
    {
        for(let j = 0; j < N; j++)
        {
            if(board[i][j] == 1)
                console.log("Q ")
            else
                console.log(". ")
        }

    }
}

// A utility function to check if a queen can
// be placed on board[row][col]. Note that this
// function is called when "col" queens are
// already placed in columns from 0 to col -1.
// So we need to check only left side for
// attacking queens
function isSafe(board, row, col)
{

    // Check this row on left side
    for(let i = 0; i < col; i++){
        if(board[row][i] == 1)
            return false
    }

    // Check upper diagonal on left side
    for (i = row, j = col; i >= 0 && j >= 0; i--, j--)
        if (board[i][j])
            return false

    // Check lower diagonal on left side
    for (i = row, j = col; j >= 0 && i < N; i++, j--)
        if (board[i][j])
            return false

    return true
}

function solveNQUtil(board, col){

    // base case: If all queens are placed
    // then return true
    if(col >= N)
        return true

    // Consider this column and try placing
    // this queen in all rows one by one
    for(let i=0;i<N;i++){

        if(isSafe(board, i, col)==true){

            // Place this queen in board[i][col]
            board[i][col] = 1

            // recur to place rest of the queens
            if(solveNQUtil(board, col + 1) == true)
                return true

            // If placing queen in board[i][col
            // doesn't lead to a solution, then
            // queen from board[i][col]
            board[i][col] = 0
        }
    }
    // if the queen can not be placed in any row in
    // this column col then return false
    return false
}

// This function solves the N Queen problem using
// Backtracking. It mainly uses solveNQUtil() to
// solve the problem. It returns false if queens
// cannot be placed, otherwise return true and
// placement of queens in the form of 1s.
// note that there may be more than one
// solutions, this function prints one of the
// feasible solutions.
function solveNQ(){
    let board = [ [0, 0, 0, 0],
            [0, 0, 0, 0],
            [0, 0, 0, 0],
            [0, 0, 0, 0] ]

    if(solveNQUtil(board, 0) == false){
        console.log("Solution does not exist")
        return false
    }

    printSolution(board)
    return true
}

// Driver Code
solveNQ()

// This code is contributed by shinjanpatra

Output

. 
. 
Q 
. 
Q 
. 
. 
. 
. 
. 
. 
Q 
. 
Q 
. 
. 

5. Dynamic Programming in javascript:

Dynamic Programming is mainly an optimization over plain recursion. Wherever we see a recursive solution that has repeated calls for same inputs, we can optimize it using Dynamic Programming. The idea is to simply store the results of subproblems, so that we do not have to re-compute them when needed later. This simple optimization reduces time complexities from exponential to polynomial.

Dynamic Programming

Standard problems on Dynamic Programming:

1. Fibonacci numbers
2. nth Catalan Number
3. Bell Numbers (Number of Ways to Partition a Set)
4. Binomial Coefficient
5. Coin change problem
6. Subset Sum Problem

5.1) nth Catalan Number in javascript:

Catalan numbers are defined as a mathematical sequence that consists of positive integers, which can be used to find the number of possibilities of various combinations. 

The nth term in the sequence denoted C_n, is found in the following formula:

The first few Catalan numbers for n = 0, 1, 2, 3, … are : 1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862, … 

Below is the implementation of the Nth Catalan number in javascript:

Javascript

// Javascript Program for nth
// Catalan Number

// A recursive function to
// find nth catalan number
function catalan(n)
{

    // Base case
    if (n <= 1)
        return 1;

    // catalan(n) is sum of
    // catalan(i)*catalan(n-i-1)
    let res = 0;
    for(let i = 0; i < n; i++)
        res += catalan(i) *
                catalan(n - i - 1);

    return res;
}

// Driver Code
for (let i = 0; i < 10; i++)
    console.log(catalan(i) + " ");

// This code is contributed _saurabh_jaiswal

Output

1 
1 
2 
5 
14 
42 
132 
429 
1430 
4862 

5.2) Binomial Coefficient in javascript:

A binomial coefficient C(n, k) can be defined as the coefficient of x^k in the expansion of (1 + x)^n.

A binomial coefficient C(n, k) also gives the number of ways, disregarding order, that k objects can be chosen from among n objects more formally, the number of k-element subsets (or k-combinations) of a n-element set.

Below is the implementation of the Binomial coefficient in javascript:

Javascript

// A Dynamic Programming based
// solution that uses table C to
// calculate the Binomial Coefficient

// Returns value of Binomial
// Coefficient C(n, k)
function binomialCoeff(n, k)
{
    var C = Array(n + 1).fill(0).map(
    x => Array(k + 1).fill(0));;
    var i, j;

    // Calculate value of Binomial
    // Coefficient in bottom up manner
    for(i = 0; i <= n; i++)
    {
        for(j = 0; j <= min(i, k); j++)
        {

            // Base Cases
            if (j == 0 || j == i)
                C[i][j] = 1;

            // Calculate value using
            // previously stored values
            else
                C[i][j] = C[i - 1][j - 1] +
                        C[i - 1][j];
        }
    }
    return C[n][k];
}

// A utility function to return
// minimum of two integers
function min(a, b)
{
    return (a < b) ? a : b;
}

// Driver code
var n = 5, k = 2;
console.log("Value of C(" + n + "," + k +
                    ") is " + binomialCoeff(n, k));

// This code is contributed by 29AjayKumar

Output

Value of C(5,2) is 10

5.3) Subset Sum Problem in javascript :

Given a set of non-negative integers and a value sum, the task is to check if there is a subset of the given set whose sum is equal to the given sum. 

Below is the implementation of the Subset Sum Problem in javascript:

Javascript

// A Dynamic Programming solution for subset sum problem

    // Returns true if there is a subset of
    // set[] with sum equal to given sum
    function isSubsetSum(set, n, sum)
    {
        // The value of subset[i][j] will be
        // true if there is a subset of
        // set[0..j-1] with sum equal to i
        let subset = new Array(sum + 1);

        for(let i = 0; i < sum + 1; i++)
        {
            subset[i] = new Array(sum + 1);
            for(let j = 0; j < n + 1; j++)
            {
                subset[i][j] = 0;
            }
        }

        // If sum is 0, then answer is true
        for (let i = 0; i <= n; i++)
            subset[0][i] = true;

        // If sum is not 0 and set is empty,
        // then answer is false
        for (let i = 1; i <= sum; i++)
            subset[i][0] = false;

        // Fill the subset table in bottom
        // up manner
        for (let i = 1; i <= sum; i++) {
            for (let j = 1; j <= n; j++) {
                subset[i][j] = subset[i][j - 1];
                if (i >= set[j - 1])
                    subset[i][j] = subset[i][j]
                                || subset[i - set[j - 1]][j - 1];
            }
        }

        return subset[sum][n];
    }

    let set = [ 3, 34, 4, 12, 5, 2 ];
    let sum = 9;
    let n = set.length;
    if (isSubsetSum(set, n, sum) == true)
    console.log("Found a subset" + " with given sum");
    else
    console.log("No subset with" + " given sum");

    // This code is contributed by decode2207.

Output

Found a subset with given sum

6. Mathematical Algorithms in javascript:

Standard problems on Mathematical algorithms:

1. Prime Numbers
2. Sieve of Eratosthenes
3. LCM of array
4. GCD of array
5. Program to add two polynomials
6. Check divisibility by 7
7. Euclidean algorithms
8. Generate Pythagorean Triplets

6.1) Prime numbers in javascript:

Prime numbers

Below is the implementation of the Prime number in javascript:

Javascript

//javascript program for prime number
    function isPrime(n) {
        // Corner case
        if (n <= 1)
            return false;

        // Check from 2 to n-1
        for (let i = 2; i < n; i++)
            if (n % i == 0)
                return false;

        return true;
    }

    // Driver Code

    isPrime(11)
        ? console.log("true")
        : console.log("false");

Output

true

6.2) LCM of given array elements:

Given an array of n numbers, find the LCM of it. 

Below is the implementation of the LCM of array elements in javascript:

Javascript

// Javascript program to find LCM of n elements

// Utility function to find
// GCD of 'a' and 'b'
function gcd(a, b)
{
    if (b == 0)
        return a;
    return gcd(b, a % b);
}

// Returns LCM of array elements
function findlcm(arr, n)
{
    // Initialize result
    let ans = arr[0];

    // ans contains LCM of arr[0], ..arr[i]
    // after i'th iteration,
    for (let i = 1; i < n; i++)
        ans = (((arr[i] * ans)) /
                (gcd(arr[i], ans)));

    return ans;
}

// Driver Code

    let arr = [ 2, 7, 3, 9, 4 ];
    let n = arr.length;
    console.log(findlcm(arr, n));

// This code is contributed by Mayank Tyagi

Output

252

6.3) Euclidean algorithm:

The Euclidean algorithm is a way to find the greatest common divisor of two positive integers. GCD of two numbers is the largest number that divides both of them. A simple way to find GCD is to factorize both numbers and multiply common prime factors.

Below is the implementation of the Euclidean algorithm in javascript:

Javascript

// Javascript program to demonstrate
// working of extended
// Euclidean Algorithm

// Javascript function for
// extended Euclidean
// Algorithm
function gcdExtended(a, b,
                    x, y)
{
    // Base Case
    if (a == 0)
    {
        x = 0;
        y = 1;
        return b;
    }

    // To store results
    // of recursive call
    let gcd = gcdExtended(b % a,
                    a, x, y);

    // Update x and y using
    // results of recursive
    // call
    x = y - (b / a) * x;
    y = x;

    return gcd;
}

// Driver Code
let x = 0;
let y = 0;
let a = 35;
let b = 15;
let g = gcdExtended(a, b, x, y);
console.log("gcd(" + a);
console.log(", " + b + ")");
console.log(" = " + g);

Output

gcd(35
, 15)
 = 5

7. Bitwise Algorithms in javascript: 

Standard Problems on Bit Algorithms:

1. Count set bits in an integer
2. Add two-bit strings
3. Turn off the rightmost set bit
4. Rotate bits of a number
5. Program to find parity
6. Check if a number is Bleak

7.1) Count set bits in an integer:

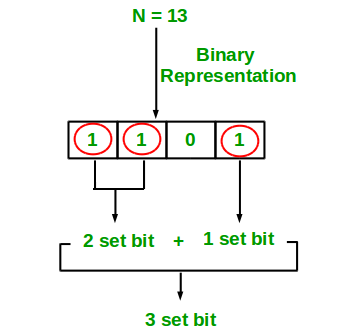
count set bit

Below is the implementation of the Count set bits in an integer in javascript:

Javascript

// JavaScript program to Count set
// bits in an integerclass

/* Function to get no of set
bits in binary representation
of passed binary no. */

function countSetBits(n)
{
    var count = 0;
    while (n > 0)
    {
        n &= (n - 1);
        count++;
    }
    return count;
}

// driver program
var i = 9;
console.log(countSetBits(i));

// This code is contributed by 29AjayKumar

Output

2

7.2) Add two bit strings:

Given two bit sequences as strings, write a function to return the addition of the two sequences. Bit strings can be of different lengths also. For example, if string 1 is “1100011” and second string 2 is “10”, then the function should return “1100101”. 

Below is the implementation of the Add two-bit strings in javascript:

Javascript

// JavaScript code to implement the approach

// Helper method: given two unequal sized bit strings, converts them to
// same length by adding leading 0s in the smaller string. Returns the
// new length
function makeEqualLength(str1, str2)
{
    var len1 = str1.length;
    var len2 = str2.length;
    if (len1 < len2)
    {
        for (var i = 0 ; i < len2 - len1 ; i++)
            str1 = '0' + str1;
        return len2;
    }
    else if (len1 > len2)
    {
        for (var i = 0 ; i < len1 - len2 ; i++)
            str2 = '0' + str2;
    }
    return len1; // If len1 >= len2
}

// The main function that adds two-bit sequences and returns the addition
function addBitStrings(first, second )
{
    var result = ""; // To store the sum bits

    // make the lengths same before adding
    var length = makeEqualLength(first, second);

    var carry = 0; // Initialize carry

    // Add all bits one by one
    for (var i = length-1 ; i >= 0 ; i--)
    {
        var firstBit = first[i] - '0';
        var secondBit = second[i] - '0';

        // boolean expression for sum of 3 bits
        var sum = (firstBit ^ secondBit ^ carry) + 48;

        result += String.fromCharCode(sum);

        // boolean expression for 3-bit addition
        carry = (firstBit & secondBit) | (secondBit & carry) | (firstBit & carry);
    }

    // if overflow, then add a leading 1
    if (carry)
        result += '1';

    return result;
}

// Driver program to test above functions
var str1 = "1100011";
var str2 = "10";

console.log("Sum is " + addBitStrings(str1, str2));

// This code is contributed by phasing17

Output

Sum is 11000101

7.3) Program to find parity  in javascript:

Parity: Parity of a number refers to whether it contains an odd or even number of 1-bits. The number has “odd parity” if it contains an odd number of 1-bits and is “even parity” if it contains an even number of 1-bits. 

Below is the implementation of the find parity in javascript:

Javascript

// Javascript program to find parity
// of an integer

// Function to get parity of number n.
// It returns 1 if n has odd parity, and
// returns 0 if n has even parity
function getParity(n)
{
    var parity = false;
    while(n != 0)
    {
        parity = !parity;
        n = n & (n - 1);
    }
    return parity;
}

// Driver code
var n = 7;
console.log("Parity of no " + n + " = " +
            (getParity(n) ? "odd": "even"));

// This code is contributed by Kirti

Output

Parity of no 7 = odd

Frequently Asked Questions (FAQs) – DSA using JavaScript Tutorial

1. What is the prerequisite knowledge for this tutorial?

• Basic understanding of JavaScript syntax, variables, loops, and functions is recommended. Familiarity with fundamental programming concepts is beneficial.

2. Do I need any specific software or tools to follow along?

• A code editor (e.g., Visual Studio Code, Sublime Text) and a JavaScript runtime environment (e.g., Node.js) are sufficient. No special tools are required.

3. Is this tutorial suitable for beginners?

• Yes, this tutorial is designed to be beginner-friendly. It starts with fundamental concepts and gradually progresses to more advanced topics.

4. How can I practice the algorithms covered in the tutorial?

• Practice by implementing the algorithms in a code editor, running them in a JavaScript environment, and experimenting with variations. Leverage coding platforms like LeetCode for additional challenges.

5. Are there any coding exercises or challenges included?

• Yes, each section includes practice problems to reinforce your understanding. Additional challenges are encouraged for further practice.

6. Can I use this tutorial for interview preparation?

• Absolutely! Understanding and practicing these algorithms will significantly contribute to your interview preparation for technical roles.

7. Are there any forums or communities to discuss the tutorial content?

• Join online coding communities like Stack Overflow, Reddit (r/learnjavascript), or platforms like Discord where you can discuss concepts, seek help, and share your solutions.

8. How do I handle difficulties or challenges in understanding certain topics?

• If you encounter challenges, revisit the explanations, experiment with the code, and seek help from online communities. Sometimes, discussing problems with others can provide valuable insights.

9. Is it necessary to complete the tutorial in order, or can I skip sections?

• While it’s recommended to follow the tutorial in order to build a solid foundation, you can skip to specific sections based on your needs. However, ensure you have a good understanding of the skipped topics.

10. What’s the best way to apply these algorithms in real-world projects?

• Identify opportunities in your projects where these algorithms can be applied. For example, sorting and searching algorithms in data processing, or graph algorithms in network analysis. Practice integrating them into practical scenarios.

11. How often should I revisit the tutorial for reinforcement?

• Regular reinforcement is beneficial. Consider revisiting the tutorial, solving additional problems, and exploring advanced topics as you gain more experience in programming and problem-solving.

12. Can I use this tutorial as a reference for technical interviews?

• Yes, this tutorial can serve as a valuable reference for technical interviews. Practice implementing algorithms and explaining your thought process, which is often a crucial aspect of technical interviews.

Feel free to ask additional questions or seek clarification on any topic throughout your learning journey. Happy coding!