Definition of Algorithm
The word Algorithm means ” A set of finite rules or instructions to be followed in calculations or other problem-solving operations ”
Or
” A procedure for solving a mathematical problem in a finite number of steps that frequently involves recursive operations”.
Therefore Algorithm refers to a sequence of finite steps to solve a particular problem.
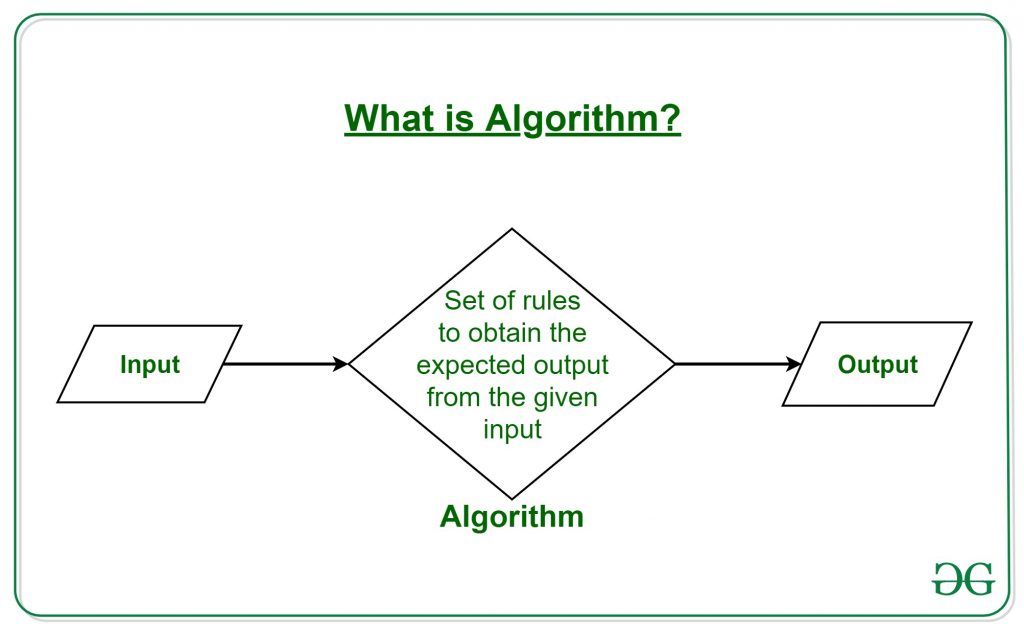
Use of the Algorithms:
Algorithms play a crucial role in various fields and have many applications. Some of the key areas where algorithms are used include:
- Computer Science: Algorithms form the basis of computer programming and are used to solve problems ranging from simple sorting and searching to complex tasks such as artificial intelligence and machine learning.
- Mathematics: Algorithms are used to solve mathematical problems, such as finding the optimal solution to a system of linear equations or finding the shortest path in a graph.
- Operations Research: Algorithms are used to optimize and make decisions in fields such as transportation, logistics, and resource allocation.
- Artificial Intelligence: Algorithms are the foundation of artificial intelligence and machine learning, and are used to develop intelligent systems that can perform tasks such as image recognition, natural language processing, and decision-making.
- Data Science: Algorithms are used to analyze, process, and extract insights from large amounts of data in fields such as marketing, finance, and healthcare.
These are just a few examples of the many applications of algorithms. The use of algorithms is continually expanding as new technologies and fields emerge, making it a vital component of modern society.
Algorithms can be simple and complex depending on what you want to achieve.
It can be understood by taking the example of cooking a new recipe. To cook a new recipe, one reads the instructions and steps and executes them one by one, in the given sequence. The result thus obtained is the new dish is cooked perfectly. Every time you use your phone, computer, laptop, or calculator you are using Algorithms. Similarly, algorithms help to do a task in programming to get the expected output.
The Algorithm designed are language-independent, i.e. they are just plain instructions that can be implemented in any language, and yet the output will be the same, as expected.
What is the need for algorithms?
- Algorithms are necessary for solving complex problems efficiently and effectively.
- They help to automate processes and make them more reliable, faster, and easier to perform.
- Algorithms also enable computers to perform tasks that would be difficult or impossible for humans to do manually.
- They are used in various fields such as mathematics, computer science, engineering, finance, and many others to optimize processes, analyze data, make predictions, and provide solutions to problems.
What are the Characteristics of an Algorithm?

As one would not follow any written instructions to cook the recipe, but only the standard one. Similarly, not all written instructions for programming are an algorithm. For some instructions to be an algorithm, it must have the following characteristics:
- Clear and Unambiguous: The algorithm should be unambiguous. Each of its steps should be clear in all aspects and must lead to only one meaning.
- Well-Defined Inputs: If an algorithm says to take inputs, it should be well-defined inputs. It may or may not take input.
- Well-Defined Outputs: The algorithm must clearly define what output will be yielded and it should be well-defined as well. It should produce at least 1 output.
- Finite-ness: The algorithm must be finite, i.e. it should terminate after a finite time.
- Feasible: The algorithm must be simple, generic, and practical, such that it can be executed with the available resources. It must not contain some future technology or anything.
- Language Independent: The Algorithm designed must be language-independent, i.e. it must be just plain instructions that can be implemented in any language, and yet the output will be the same, as expected.
- Input: An algorithm has zero or more inputs. Each that contains a fundamental operator must accept zero or more inputs.
- Output: An algorithm produces at least one output. Every instruction that contains a fundamental operator must accept zero or more inputs.
- Definiteness: All instructions in an algorithm must be unambiguous, precise, and easy to interpret. By referring to any of the instructions in an algorithm one can clearly understand what is to be done. Every fundamental operator in instruction must be defined without any ambiguity.
- Finiteness: An algorithm must terminate after a finite number of steps in all test cases. Every instruction which contains a fundamental operator must be terminated within a finite amount of time. Infinite loops or recursive functions without base conditions do not possess finiteness.
- Effectiveness: An algorithm must be developed by using very basic, simple, and feasible operations so that one can trace it out by using just paper and pencil.
Properties of Algorithm:
- It should terminate after a finite time.
- It should produce at least one output.
- It should take zero or more input.
- It should be deterministic means giving the same output for the same input case.
- Every step in the algorithm must be effective i.e. every step should do some work.
Types of Algorithms:
There are several types of algorithms available. Some important algorithms are:
It is the simplest approach to a problem. A brute force algorithm is the first approach that comes to finding when we see a problem.
A recursive algorithm is based on recursion. In this case, a problem is broken into several sub-parts and called the same function again and again.
The backtracking algorithm builds the solution by searching among all possible solutions. Using this algorithm, we keep on building the solution following criteria. Whenever a solution fails we trace back to the failure point build on the next solution and continue this process till we find the solution or all possible solutions are looked after.
Searching algorithms are the ones that are used for searching elements or groups of elements from a particular data structure. They can be of different types based on their approach or the data structure in which the element should be found.
Sorting is arranging a group of data in a particular manner according to the requirement. The algorithms which help in performing this function are called sorting algorithms. Generally sorting algorithms are used to sort groups of data in an increasing or decreasing manner.
Hashing algorithms work similarly to the searching algorithm. But they contain an index with a key ID. In hashing, a key is assigned to specific data.
This algorithm breaks a problem into sub-problems, solves a single sub-problem, and merges the solutions to get the final solution. It consists of the following three steps:
In this type of algorithm, the solution is built part by part. The solution for the next part is built based on the immediate benefit of the next part. The one solution that gives the most benefit will be chosen as the solution for the next part.
This algorithm uses the concept of using the already found solution to avoid repetitive calculation of the same part of the problem. It divides the problem into smaller overlapping subproblems and solves them.
In the randomized algorithm, we use a random number so it gives immediate benefit. The random number helps in deciding the expected outcome.
To learn more about the types of algorithms refer to the article about “Types of Algorithms“.
Advantages of Algorithms:
- It is easy to understand.
- An algorithm is a step-wise representation of a solution to a given problem.
- In an Algorithm the problem is broken down into smaller pieces or steps hence, it is easier for the programmer to convert it into an actual program.
Disadvantages of Algorithms:
- Writing an algorithm takes a long time so it is time-consuming.
- Understanding complex logic through algorithms can be very difficult.
- Branching and Looping statements are difficult to show in Algorithms(imp).
How to Design an Algorithm?
To write an algorithm, the following things are needed as a pre-requisite:
- The problem that is to be solved by this algorithm i.e. clear problem definition.
- The constraints of the problem must be considered while solving the problem.
- The input to be taken to solve the problem.
- The output is to be expected when the problem is solved.
- The solution to this problem is within the given constraints.
Then the algorithm is written with the help of the above parameters such that it solves the problem.
Example: Consider the example to add three numbers and print the sum.
Step 1: Fulfilling the pre-requisites
As discussed above, to write an algorithm, its prerequisites must be fulfilled.
- The problem that is to be solved by this algorithm: Add 3 numbers and print their sum.
- The constraints of the problem that must be considered while solving the problem: The numbers must contain only digits and no other characters.
- The input to be taken to solve the problem: The three numbers to be added.
- The output to be expected when the problem is solved: The sum of the three numbers taken as the input i.e. a single integer value.
- The solution to this problem, in the given constraints: The solution consists of adding the 3 numbers. It can be done with the help of the ‘+’ operator, or bit-wise, or any other method.
Step 2: Designing the algorithm
Now let’s design the algorithm with the help of the above pre-requisites:
Algorithm to add 3 numbers and print their sum:
- START
- Declare 3 integer variables num1, num2, and num3.
- Take the three numbers, to be added, as inputs in variables num1, num2, and num3 respectively.
- Declare an integer variable sum to store the resultant sum of the 3 numbers.
- Add the 3 numbers and store the result in the variable sum.
- Print the value of the variable sum
- END
Step 3: Testing the algorithm by implementing it.
To test the algorithm, let’s implement it in C language.
Program:
C++
#include <bits/stdc++.h>
using namespace std;
int main()
{
int num1, num2, num3;
int sum;
cout << "Enter the 1st number: ";
cin >> num1;
cout << " " << num1 << endl;
cout << "Enter the 2nd number: ";
cin >> num2;
cout << " " << num2 << endl;
cout << "Enter the 3rd number: ";
cin >> num3;
cout << " " << num3;
sum = num1 + num2 + num3;
cout << "\nSum of the 3 numbers is: "
<< sum;
return 0;
}
|
C
#include <stdio.h>
int main()
{
int num1, num2, num3;
int sum;
printf("Enter the 1st number: ");
scanf("%d", &num1);
printf("%d\n", num1);
printf("Enter the 2nd number: ");
scanf("%d", &num2);
printf("%d\n", num2);
printf("Enter the 3rd number: ");
scanf("%d", &num3);
printf("%d\n", num3);
sum = num1 + num2 + num3;
printf("\nSum of the 3 numbers is: %d", sum);
return 0;
}
|
Java
import java.util.*;
class GFG {
public static void main(String[] args)
{
int sum = 0;
Scanner sc
= new Scanner(System.in);
System.out.println("Enter the 1st number: ");
int num1 = sc.nextInt();
System.out.println(" " + num1);
System.out.println("Enter the 2nd number: ");
int num2 = sc.nextInt();
System.out.println(" " + num2);
System.out.println("Enter the 3rd number: ");
int num3 = sc.nextInt();
System.out.println(" " + num3);
sum = num1 + num2 + num3;
System.out.println("Sum of the 3 numbers is = "
+ sum);
}
}
|
Python3
if __name__ == "__main__":
num1 = num2 = num3 = 0
sum = 0
num1 = int(input("Enter the 1st number: "))
num2 = int(input("Enter the 2nd number: "))
num3 = int(input("Enter the 3rd number: "))
sum = num1 + num2 + num3
print("\nSum of the 3 numbers is:", sum)
|
C#
using System;
class GFG {
static public void Main ()
{
int sum = 0;
Console.Write("Enter the 1st number: ");
int num1 = int.Parse(Console.ReadLine());
Console.WriteLine(" " + num1);
Console.Write("Enter the 2nd number: ");
int num2 = int.Parse(Console.ReadLine());
Console.WriteLine(" " + num2);
Console.Write("Enter the 3rd number: ");
int num3 = int.Parse(Console.ReadLine());
Console.WriteLine(" " + num3);
sum = num1 + num2 + num3;
Console.WriteLine("Sum of the 3 numbers is = "
+ sum);
}
}
|
Javascript
let num1 = 0, num2 = 0, num3 = 0;
let sum = 0;
console.log("Enter the 1st number: ");
num1 = parseInt(prompt());
console.log(" " + num1 + "<br>");
console.log("Enter the 2nd number: ");
num2=parseInt(prompt());
console.log(" " + num2 + "<br>");
console.log("Enter the 3rd number: ");
num3=parseInt(prompt());
console.log(" " + num3);
sum = num1 + num2 + num3;
console.log("<br>Sum of the 3 numbers is: " + sum);
|
OutputEnter the 1st number: 0
Enter the 2nd number: 0
Enter the 3rd number: -1577141152
Sum of the 3 numbers is: -1577141152
Here is the step-by-step algorithm of the code:
- Declare three variables num1, num2, and num3 to store the three numbers to be added.
- Declare a variable sum to store the sum of the three numbers.
- Use the cout statement to prompt the user to enter the first number.
- Use the cin statement to read the first number and store it in num1.
- Use the cout statement to prompt the user to enter the second number.
- Use the cin statement to read the second number and store it in num2.
- Use the cout statement to prompt the user to enter the third number.
- Use the cin statement to read and store the third number in num3.
- Calculate the sum of the three numbers using the + operator and store it in the sum variable.
- Use the cout statement to print the sum of the three numbers.
- The main function returns 0, which indicates the successful execution of the program.
Time complexity: O(1)
Auxiliary Space: O(1)
One problem, many solutions: The solution to an algorithm can be or cannot be more than one. It means that while implementing the algorithm, there can be more than one method to implement it. For example, in the above problem of adding 3 numbers, the sum can be calculated in many ways:
- + operator
- Bit-wise operators
- . . etc
How to analyze an Algorithm?
For a standard algorithm to be good, it must be efficient. Hence the efficiency of an algorithm must be checked and maintained. It can be in two stages:
1. Priori Analysis:
“Priori” means “before”. Hence Priori analysis means checking the algorithm before its implementation. In this, the algorithm is checked when it is written in the form of theoretical steps. This Efficiency of an algorithm is measured by assuming that all other factors, for example, processor speed, are constant and have no effect on the implementation. This is done usually by the algorithm designer. This analysis is independent of the type of hardware and language of the compiler. It gives the approximate answers for the complexity of the program.
2. Posterior Analysis:
“Posterior” means “after”. Hence Posterior analysis means checking the algorithm after its implementation. In this, the algorithm is checked by implementing it in any programming language and executing it. This analysis helps to get the actual and real analysis report about correctness(for every possible input/s if it shows/returns correct output or not), space required, time consumed, etc. That is, it is dependent on the language of the compiler and the type of hardware used.
What is Algorithm complexity and how to find it?
An algorithm is defined as complex based on the amount of Space and Time it consumes. Hence the Complexity of an algorithm refers to the measure of the time that it will need to execute and get the expected output, and the Space it will need to store all the data (input, temporary data, and output). Hence these two factors define the efficiency of an algorithm.
The two factors of Algorithm Complexity are:
- Time Factor: Time is measured by counting the number of key operations such as comparisons in the sorting algorithm.
- Space Factor: Space is measured by counting the maximum memory space required by the algorithm to run/execute.
Therefore the complexity of an algorithm can be divided into two types:
1. Space Complexity: The space complexity of an algorithm refers to the amount of memory required by the algorithm to store the variables and get the result. This can be for inputs, temporary operations, or outputs.
How to calculate Space Complexity?
The space complexity of an algorithm is calculated by determining the following 2 components:
- Fixed Part: This refers to the space that is required by the algorithm. For example, input variables, output variables, program size, etc.
- Variable Part: This refers to the space that can be different based on the implementation of the algorithm. For example, temporary variables, dynamic memory allocation, recursion stack space, etc.
Therefore Space complexity S(P) of any algorithm P is S(P) = C + SP(I), where C is the fixed part and S(I) is the variable part of the algorithm, which depends on instance characteristic I.
Example: Consider the below algorithm for Linear Search
Step 1: START
Step 2: Get n elements of the array in arr and the number to be searched in x
Step 3: Start from the leftmost element of arr[] and one by one compare x with each element of arr[]
Step 4: If x matches with an element, Print True.
Step 5: If x doesn’t match with any of the elements, Print False.
Step 6: END
Here, There are 2 variables arr[], and x, where the arr[] is the variable part of n elements and x is the fixed part. Hence S(P) = 1+n. So, the space complexity depends on n(number of elements). Now, space depends on data types of given variables and constant types and it will be multiplied accordingly.
2. Time Complexity: The time complexity of an algorithm refers to the amount of time required by the algorithm to execute and get the result. This can be for normal operations, conditional if-else statements, loop statements, etc.
How to Calculate, Time Complexity?
The time complexity of an algorithm is also calculated by determining the following 2 components:
- Constant time part: Any instruction that is executed just once comes in this part. For example, input, output, if-else, switch, arithmetic operations, etc.
- Variable Time Part: Any instruction that is executed more than once, say n times, comes in this part. For example, loops, recursion, etc.
Therefore Time complexity 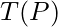 of any algorithm P is T(P) = C + TP(I), where C is the constant time part and TP(I) is the variable part of the algorithm, which depends on the instance characteristic I.
of any algorithm P is T(P) = C + TP(I), where C is the constant time part and TP(I) is the variable part of the algorithm, which depends on the instance characteristic I.
Example: In the algorithm of Linear Search above, the time complexity is calculated as follows:
Step 1: –Constant Time
Step 2: — Variable Time (Taking n inputs)
Step 3: –Variable Time (Till the length of the Array (n) or the index of the found element)
Step 4: –Constant Time
Step 5: –Constant Time
Step 6: –Constant Time
Hence, T(P) = 1 + n + n(1 + 1) + 1 = 2 + 3n, which can be said as T(n).
How to express an Algorithm?
- Natural Language:- Here we express the Algorithm in the natural English language. It is too hard to understand the algorithm from it.
- Flow Chart:- Here we express the Algorithm by making a graphical/pictorial representation of it. It is easier to understand than Natural Language.
- Pseudo Code:- Here we express the Algorithm in the form of annotations and informative text written in plain English which is very much similar to the real code but as it has no syntax like any of the programming languages, it can’t be compiled or interpreted by the computer. It is the best way to express an algorithm because it can be understood by even a layman with some school-level knowledge.
Share your thoughts in the comments
Please Login to comment...