Euclidean algorithms (Basic and Extended)

Difficulty Level : Medium
Last Updated : 01 Sep, 2022

The Euclidean algorithm is a way to find the greatest common divisor of two positive integers. GCD of two numbers is the largest number that divides both of them. A simple way to find GCD is to factorize both numbers and multiply common prime factors.

GCD

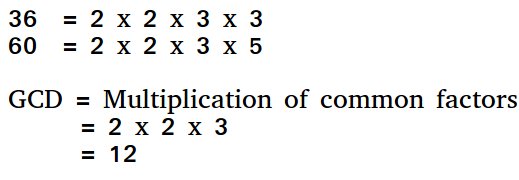
Basic Euclidean Algorithm for GCD:

The algorithm is based on the below facts.

If we subtract a smaller number from a larger one (we reduce a larger number), GCD doesn’t change. So if we keep subtracting repeatedly the larger of two, we end up with GCD.
Now instead of subtraction, if we divide the smaller number, the algorithm stops when we find the remainder 0.

Below is a recursive function to evaluate gcd using Euclid’s algorithm:

C

// C program to demonstrate Basic Euclidean Algorithm
#include <stdio.h>
 
// Function to return gcd of a and b
int gcd(int a, int b)
{
    if (a == 0)
        return b;
    return gcd(b % a, a);
}
 
// Driver code
int main()
{
    int a = 10, b = 15;
   
      // Function call
    printf("GCD(%d, %d) = %d\n", a, b, gcd(a, b));
    a = 35, b = 10;
    printf("GCD(%d, %d) = %d\n", a, b, gcd(a, b));
    a = 31, b = 2;
    printf("GCD(%d, %d) = %d\n", a, b, gcd(a, b));
    return 0;
}

CPP

// C++ program to demonstrate
// Basic Euclidean Algorithm
 
#include <bits/stdc++.h>
using namespace std;
 
// Function to return
// gcd of a and b
int gcd(int a, int b)
{
    if (a == 0)
        return b;
    return gcd(b % a, a);
}
 
// Driver Code
int main()
{
    int a = 10, b = 15;
   
      // Function call
    cout << "GCD(" << a << ", " << b << ") = " << gcd(a, b)
         << endl;
    a = 35, b = 10;
    cout << "GCD(" << a << ", " << b << ") = " << gcd(a, b)
         << endl;
    a = 31, b = 2;
    cout << "GCD(" << a << ", " << b << ") = " << gcd(a, b)
         << endl;
    return 0;
}

Java

// Java program to demonstrate Basic Euclidean Algorithm
 
import java.lang.*;
import java.util.*;
 
class GFG {
    // extended Euclidean Algorithm
    public static int gcd(int a, int b)
    {
        if (a == 0)
            return b;
 
        return gcd(b % a, a);
    }
 
    // Driver code
    public static void main(String[] args)
    {
        int a = 10, b = 15, g;
       
          // Function call
        g = gcd(a, b);
        System.out.println("GCD(" + a + " , " + b
                           + ") = " + g);
 
        a = 35;
        b = 10;
        g = gcd(a, b);
        System.out.println("GCD(" + a + " , " + b
                           + ") = " + g);
 
        a = 31;
        b = 2;
        g = gcd(a, b);
        System.out.println("GCD(" + a + " , " + b
                           + ") = " + g);
    }
}
// Code Contributed by Mohit Gupta_OMG <(0_o)>

Python3

# Python3 program to demonstrate Basic Euclidean Algorithm
 
 
# Function to return gcd of a and b
def gcd(a, b):
    if a == 0:
        return b
 
    return gcd(b % a, a)
 
# Driver code
if __name__ == "__main__":
  a = 10
  b = 15
  print("gcd(", a, ",", b, ") = ", gcd(a, b))
 
  a = 35
  b = 10
  print("gcd(", a, ",", b, ") = ", gcd(a, b))
 
  a = 31
  b = 2
  print("gcd(", a, ",", b, ") = ", gcd(a, b))
 
# Code Contributed By Mohit Gupta_OMG <(0_o)>

C#

// C# program to demonstrate Basic Euclidean Algorithm
 
using System;
 
class GFG {
    public static int gcd(int a, int b)
    {
        if (a == 0)
            return b;
 
        return gcd(b % a, a);
    }
 
    // Driver Code
    static public void Main()
    {
        int a = 10, b = 15, g;
        g = gcd(a, b);
        Console.WriteLine("GCD(" + a + " , " + b
                          + ") = " + g);
 
        a = 35;
        b = 10;
        g = gcd(a, b);
        Console.WriteLine("GCD(" + a + " , " + b
                          + ") = " + g);
 
        a = 31;
        b = 2;
        g = gcd(a, b);
        Console.WriteLine("GCD(" + a + " , " + b
                          + ") = " + g);
    }
}
 
// This code is contributed by ajit

PHP

// php program to demonstrate Basic Euclidean Algorithm
 
<?php
// PHP program to demonstrate
// Basic Euclidean Algorithm
 
// Function to return
// gcd of a and b
function gcd($a, $b)
{
    if ($a == 0)
        return $b;
    return gcd($b % $a, $a);
}
 
// Driver Code
$a = 10; $b = 15;
 
// Function call
echo "GCD(",$a,"," , $b,") = ",
                   gcd($a, $b);
echo "\n";
$a = 35; $b = 10;
echo "GCD(",$a ,",",$b,") = ",
                  gcd($a, $b);
echo "\n";
$a = 31; $b = 2;
echo "GCD(",$a ,",", $b,") = ",
                   gcd($a, $b);
 
// This code is contributed by m_kit
?>

Javascript

// JavaScript program to demonstrate
// Basic Euclidean Algorithm
 
// Function to return
// gcd of a and b
function gcd( a,  b)
{
    if (a == 0)
        return b;
    return gcd(b % a, a);
}
 
// Driver Code
 
    let a = 10, b = 15;
   document.write( "GCD(" + a + ", "
         + b + ") = " + gcd(a, b) +"<br/>");
          
    a = 35, b = 10;
   document.write( "GCD(" + a + ", "
         + b + ") = " + gcd(a, b) +"<br/>");
          
    a = 31, b = 2;
    document.write( "GCD(" + a + ", "
         + b + ") = " + gcd(a, b) +"<br/>");
 
// This code contributed by aashish1995

Output

GCD(10, 15) = 5
GCD(35, 10) = 5
GCD(31, 2) = 1

Time Complexity: O(Log min(a, b))
Auxiliary Space: O(Log (min(a,b))

Extended Euclidean Algorithm:

Extended Euclidean algorithm also finds integer coefficients x and y such that: ax + by = gcd(a, b)

Examples:

Input: a = 30, b = 20
Output: gcd = 10, x = 1, y = -1
(Note that 30*1 + 20*(-1) = 10)
Input: a = 35, b = 15
Output: gcd = 5, x = 1, y = -2
(Note that 35*1 + 15*(-2) = 5)

The extended Euclidean algorithm updates the results of gcd(a, b) using the results calculated by the recursive call gcd(b%a, a). Let values of x and y calculated by the recursive call be x₁ and y₁. x and y are updated using the below expressions.

ax + by = gcd(a, b)
gcd(a, b) = gcd(b%a, a)
gcd(b%a, a) = (b%a)x₁+ ay₁
ax + by = (b%a)x₁+ ay₁
ax + by = (b – [b/a] * a)x₁+ ay₁
ax + by = a(y₁ – [b/a] * x₁) + bx₁
Comparing LHS and RHS,
x = y₁ – ⌊b/a⌋ * x₁
y = x₁

Below is an implementation of the above approach:

C++

// C++ program to demonstrate working of
// extended Euclidean Algorithm
#include <bits/stdc++.h>
using namespace std;
 
// Function for extended Euclidean Algorithm
int gcdExtended(int a, int b, int *x, int *y)
{
    // Base Case
    if (a == 0)
    {
        *x = 0;
        *y = 1;
        return b;
    }
 
    int x1, y1; // To store results of recursive call
    int gcd = gcdExtended(b%a, a, &x1, &y1);
 
    // Update x and y using results of
    // recursive call
    *x = y1 - (b/a) * x1;
    *y = x1;
 
    return gcd;
}
 
// Driver Code
int main()
{
    int x, y, a = 35, b = 15;
    int g = gcdExtended(a, b, &x, &y);
    cout << "GCD(" << a << ", " << b
         << ") = " << g << endl;
    return 0;
}

C

// C program to demonstrate working of extended
// Euclidean Algorithm
#include <stdio.h>
 
// C function for extended Euclidean Algorithm
int gcdExtended(int a, int b, int *x, int *y)
{
    // Base Case
    if (a == 0)
    {
        *x = 0;
        *y = 1;
        return b;
    }
 
    int x1, y1; // To store results of recursive call
    int gcd = gcdExtended(b%a, a, &x1, &y1);
 
    // Update x and y using results of recursive
    // call
    *x = y1 - (b/a) * x1;
    *y = x1;
 
    return gcd;
}
 
// Driver Program
int main()
{
    int x, y;
    int a = 35, b = 15;
    int g = gcdExtended(a, b, &x, &y);
    printf("gcd(%d, %d) = %d", a, b, g);
    return 0;
}

Java

// Java program to demonstrate working of extended
// Euclidean Algorithm
 
import java.lang.*;
import java.util.*;
 
class GFG {
    // extended Euclidean Algorithm
    public static int gcdExtended(int a, int b, int x,
                                  int y)
    {
        // Base Case
        if (a == 0) {
            x = 0;
            y = 1;
            return b;
        }
 
        int x1 = 1,
            y1 = 1; // To store results of recursive call
        int gcd = gcdExtended(b % a, a, x1, y1);
 
        // Update x and y using results of recursive
        // call
        x = y1 - (b / a) * x1;
        y = x1;
 
        return gcd;
    }
 
    // Driver Program
    public static void main(String[] args)
    {
        int x = 1, y = 1;
        int a = 35, b = 15;
        int g = gcdExtended(a, b, x, y);
        System.out.print("gcd(" + a + " , " + b
                         + ") = " + g);
    }
}

Python3

# Python program to demonstrate working of extended
# Euclidean Algorithm
 
# function for extended Euclidean Algorithm
 
 
def gcdExtended(a, b):
 
    # Base Case
    if a == 0:
        return b, 0, 1
 
    gcd, x1, y1 = gcdExtended(b % a, a)
 
    # Update x and y using results of recursive
    # call
    x = y1 - (b//a) * x1
    y = x1
 
    return gcd, x, y
 
 
# Driver code
a, b = 35, 15
g, x, y = gcdExtended(a, b)
print("gcd(", a, ",", b, ") = ", g)

C#

// C# program to demonstrate working
// of extended Euclidean Algorithm
using System;
 
class GFG
{
     
    // extended Euclidean Algorithm
    public static int gcdExtended(int a, int b,
                                  int x, int y)
    {
        // Base Case
        if (a == 0)
        {
            x = 0;
            y = 1;
            return b;
        }
 
        // To store results of
        // recursive call
        int x1 = 1, y1 = 1;
        int gcd = gcdExtended(b % a, a, x1, y1);
 
        // Update x and y using
        // results of recursive call
        x = y1 - (b / a) * x1;
        y = x1;
 
        return gcd;
    }
     
    // Driver Code
    static public void Main ()
    {
        int x = 1, y = 1;
        int a = 35, b = 15;
        int g = gcdExtended(a, b, x, y);
        Console.WriteLine("gcd(" + a + " , " +
                              b + ") = " + g);
    }
}

PHP

<?php
// PHP program to demonstrate
// working of extended
// Euclidean Algorithm
 
// PHP function for
// extended Euclidean
// Algorithm
function gcdExtended($a, $b,   
                     $x, $y)
{
    // Base Case
    if ($a == 0)
    {
        $x = 0;
        $y = 1;
        return $b;
    }
 
    // To store results
    // of recursive call
    $gcd = gcdExtended($b % $a,
                       $a, $x, $y);
 
    // Update x and y using
    // results of recursive
    // call
    $x = $y - floor($b / $a) * $x;
    $y = $x;
 
    return $gcd;
}
 
// Driver Code
$x = 0;
$y = 0;
$a = 35; $b = 15;
$g = gcdExtended($a, $b, $x, $y);
echo "gcd(",$a;
echo ", " , $b, ")";
echo " = " , $g;
 
?>

Javascript

<script>
 
// Javascript program to demonstrate
// working of extended
// Euclidean Algorithm
 
// Javascript function for
// extended Euclidean
// Algorithm
function gcdExtended(a, b,   
                     x, y)
{
    // Base Case
    if (a == 0)
    {
        x = 0;
        y = 1;
        return b;
    }
 
    // To store results
    // of recursive call
    let gcd = gcdExtended(b % a,
                       a, x, y);
 
    // Update x and y using
    // results of recursive
    // call
    x = y - (b / a) * x;
    y = x;
 
    return gcd;
}
 
// Driver Code
let x = 0;
let y = 0;
let a = 35;
let b = 15;
let g = gcdExtended(a, b, x, y);
document.write("gcd(" + a);
document.write(", " + b + ")");
document.write(" = " + g);
 
 
</script>

Output :

gcd(35, 15) = 5

Time Complexity: O(log N)
Auxiliary Space: O(log N)

How does Extended Algorithm Work?

As seen above, x and y are results for inputs a and b,
a.x + b.y = gcd —-(1)
And x₁ and y₁ are results for inputs b%a and a
(b%a).x₁ + a.y₁ = gcd
When we put b%a = (b – (⌊b/a⌋).a) in above,
we get following. Note that ⌊b/a⌋ is floor(b/a)
(b – (⌊b/a⌋).a).x₁ + a.y₁ = gcd
Above equation can also be written as below
b.x₁ + a.(y₁ – (⌊b/a⌋).x₁) = gcd —(2)
After comparing coefficients of ‘a’ and ‘b’ in (1) and
(2), we get following,
x = y₁ – ⌊b/a⌋ * x₁
y = x₁

How is Extended Algorithm Useful?

The extended Euclidean algorithm is particularly useful when a and b are coprime (or gcd is 1). Since x is the modular multiplicative inverse of “a modulo b”, and y is the modular multiplicative inverse of “b modulo a”. In particular, the computation of the modular multiplicative inverse is an essential step in RSA public-key encryption method.

This article is contributed by Ankur. Please write comments if you find anything incorrect, or if you want to share more information about the topic discussed above

My Personal Notes