Introduction to Binary Tree – Data Structure and Algorithm Tutorials
Last Updated :
20 Apr, 2023
A binary tree is a tree data structure in which each node can have at most two children, which are referred to as the left child and the right child.
The topmost node in a binary tree is called the root, and the bottom-most nodes are called leaves. A binary tree can be visualized as a hierarchical structure with the root at the top and the leaves at the bottom.
Binary trees have many applications in computer science, including data storage and retrieval, expression evaluation, network routing, and game AI. They can also be used to implement various algorithms such as searching, sorting, and graph algorithms.
Representation of Binary Tree:
Each node in the tree contains the following:
- Data
- Pointer to the left child
- Pointer to the right child

Binary Tree
In C, we can represent a tree node using structures. In other languages, we can use classes as part of their OOP feature. Below is an example of a tree node with integer data.
C
struct node {
int data;
struct node* left;
struct node* right;
};
|
C++
struct node {
int data;
struct node* left;
struct node* right;
};
class Node {
public:
int data;
Node* left;
Node* right;
};
|
Python
class Node:
def __init__(self, key):
self.left = None
self.right = None
self.val = key
|
Java
class Node {
int key;
Node left, right;
public Node(int item)
{
key = item;
left = right = null;
}
}
|
C#
class Node {
int key;
Node left, right;
public Node(int item)
{
key = item;
left = right = null;
}
}
|
Javascript
<script>
class Node
{
constructor(item)
{
this.key = item;
this.left = this.right = null;
}
}
</script>
|
Basic Operations On Binary Tree:
- Inserting an element.
- Removing an element.
- Searching for an element.
- Deletion for an element.
- Traversing an element. There are four (mainly three) types of traversals in a binary tree which will be discussed ahead.
Auxiliary Operations On Binary Tree:
- Finding the height of the tree
- Find the level of the tree
- Finding the size of the entire tree.
Applications of Binary Tree:
- In compilers, Expression Trees are used which is an application of binary trees.
- Huffman coding trees are used in data compression algorithms.
- Priority Queue is another application of binary tree that is used for searching maximum or minimum in O(1) time complexity.
- Represent hierarchical data.
- Used in editing software like Microsoft Excel and spreadsheets.
- Useful for indexing segmented at the database is useful in storing cache in the system,
- Syntax trees are used for most famous compilers for programming like GCC, and AOCL to perform arithmetic operations.
- For implementing priority queues.
- Used to find elements in less time (binary search tree)
- Used to enable fast memory allocation in computers.
- Used to perform encoding and decoding operations.
- Binary trees can be used to organize and retrieve information from large datasets, such as in inverted index and k-d trees.
- Binary trees can be used to represent the decision-making process of computer-controlled characters in games, such as in decision trees.
- Binary trees can be used to implement searching algorithms, such as in binary search trees which can be used to quickly find an element in a sorted list.
- Binary trees can be used to implement sorting algorithms, such as in heap sort which uses a binary heap to sort elements efficiently.
Binary Tree Traversals:
Tree Traversal algorithms can be classified broadly into two categories:
- Depth-First Search (DFS) Algorithms
- Breadth-First Search (BFS) Algorithms
Tree Traversal using Depth-First Search (DFS) algorithm can be further classified into three categories:
- Preorder Traversal (current-left-right): Visit the current node before visiting any nodes inside the left or right subtrees. Here, the traversal is root – left child – right child. It means that the root node is traversed first then its left child and finally the right child.
- Inorder Traversal (left-current-right): Visit the current node after visiting all nodes inside the left subtree but before visiting any node within the right subtree. Here, the traversal is left child – root – right child. It means that the left child is traversed first then its root node and finally the right child.
- Postorder Traversal (left-right-current): Visit the current node after visiting all the nodes of the left and right subtrees. Here, the traversal is left child – right child – root. It means that the left child has traversed first then the right child and finally its root node.
Tree Traversal using Breadth-First Search (BFS) algorithm can be further classified into one category:
- Level Order Traversal: Visit nodes level-by-level and left-to-right fashion at the same level. Here, the traversal is level-wise. It means that the most left child has traversed first and then the other children of the same level from left to right have traversed.
Let us traverse the following tree with all four traversal methods:
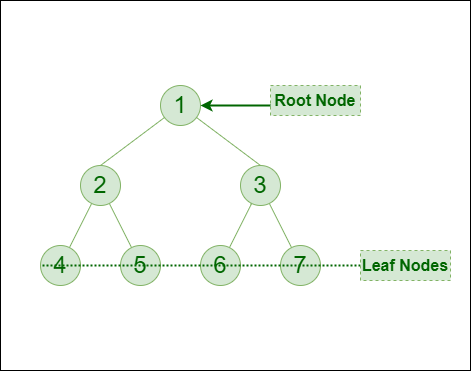
Binary Tree
Pre-order Traversal of the above tree: 1-2-4-5-3-6-7
In-order Traversal of the above tree: 4-2-5-1-6-3-7
Post-order Traversal of the above tree: 4-5-2-6-7-3-1
Level-order Traversal of the above tree: 1-2-3-4-5-6-7
Implementation of Binary Tree:
Let us create a simple tree with 4 nodes. The created tree would be as follows.

Binary Tree
Below is the Implementation of the binary tree:
C
#include <stdio.h>
#include <stdlib.h>
struct node {
int data;
struct node* left;
struct node* right;
};
struct node* newNode(int data)
{
struct node* node
= (struct node*)malloc(sizeof(struct node));
node->data = data;
node->left = NULL;
node->right = NULL;
return (node);
}
int main()
{
struct node* root = newNode(1);
root->left = newNode(2);
root->right = newNode(3);
root->left->left = newNode(4);
getchar();
return 0;
}
|
C++
#include <bits/stdc++.h>
using namespace std;
class Node {
public:
int data;
Node* left;
Node* right;
Node(int val)
{
data = val;
left = NULL;
right = NULL;
}
};
int main()
{
Node* root = new Node(1);
root->left = new Node(2);
root->right = new Node(3);
root->left->left = new Node(4);
return 0;
}
|
Java
class Node {
int key;
Node left, right;
public Node(int item)
{
key = item;
left = right = null;
}
}
class BinaryTree {
Node root;
BinaryTree(int key) { root = new Node(key); }
BinaryTree() { root = null; }
public static void main(String[] args)
{
BinaryTree tree = new BinaryTree();
tree.root = new Node(1);
tree.root.left = new Node(2);
tree.root.right = new Node(3);
tree.root.left.left = new Node(4);
}
}
|
Python
class Node:
def __init__(self, key):
self.left = None
self.right = None
self.val = key
if __name__ == '__main__':
root = Node(1)
root.left = Node(2)
root.right = Node(3)
root.left.left = Node(4)
|
C#
using System;
public class Node {
public int key;
public Node left, right;
public Node(int item)
{
key = item;
left = right = null;
}
}
public class BinaryTree {
Node root;
BinaryTree(int key) { root = new Node(key); }
BinaryTree() { root = null; }
public static void Main(String[] args)
{
BinaryTree tree = new BinaryTree();
tree.root = new Node(1);
tree.root.left = new Node(2);
tree.root.right = new Node(3);
tree.root.left.left = new Node(4);
}
}
|
Javascript
<script>
class Node {
constructor(val) {
this.key = val;
this.left = null;
this.right = null;
}
}
var root = null;
root = new Node(1);
root.left = new Node(2);
root.right = new Node(3);
root.left.left = new Node(4);
</script>
|
Conclusion:
Tree is a hierarchical data structure. Main uses of trees include maintaining hierarchical data, providing moderate access and insert/delete operations. Binary trees are special cases of tree where every node has at most two children.
What else can you read?
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...