What is Recursion?
The process in which a function calls itself directly or indirectly is called recursion and the corresponding function is called a recursive function. Using a recursive algorithm, certain problems can be solved quite easily. Examples of such problems are Towers of Hanoi (TOH), Inorder/Preorder/Postorder Tree Traversals, DFS of Graph, etc. A recursive function solves a particular problem by calling a copy of itself and solving smaller subproblems of the original problems. Many more recursive calls can be generated as and when required. It is essential to know that we should provide a certain case in order to terminate this recursion process. So we can say that every time the function calls itself with a simpler version of the original problem.
Need of Recursion
Recursion is an amazing technique with the help of which we can reduce the length of our code and make it easier to read and write. It has certain advantages over the iteration technique which will be discussed later. A task that can be defined with its similar subtask, recursion is one of the best solutions for it. For example; The Factorial of a number.
Properties of Recursion:
- Performing the same operations multiple times with different inputs.
- In every step, we try smaller inputs to make the problem smaller.
- Base condition is needed to stop the recursion otherwise infinite loop will occur.
Algorithm: Steps
The algorithmic steps for implementing recursion in a function are as follows:
Step1 - Define a base case: Identify the simplest case for which the solution is known or trivial. This is the stopping condition for the recursion, as it prevents the function from infinitely calling itself.
Step2 - Define a recursive case: Define the problem in terms of smaller subproblems. Break the problem down into smaller versions of itself, and call the function recursively to solve each subproblem.
Step3 - Ensure the recursion terminates: Make sure that the recursive function eventually reaches the base case, and does not enter an infinite loop.
step4 - Combine the solutions: Combine the solutions of the subproblems to solve the original problem.
A Mathematical Interpretation
Let us consider a problem that a programmer has to determine the sum of first n natural numbers, there are several ways of doing that but the simplest approach is simply to add the numbers starting from 1 to n. So the function simply looks like this,
approach(1) – Simply adding one by one
f(n) = 1 + 2 + 3 +……..+ n
but there is another mathematical approach of representing this,
approach(2) – Recursive adding
f(n) = 1 n=1
f(n) = n + f(n-1) n>1
There is a simple difference between the approach (1) and approach(2) and that is in approach(2) the function “ f( ) ” itself is being called inside the function, so this phenomenon is named recursion, and the function containing recursion is called recursive function, at the end, this is a great tool in the hand of the programmers to code some problems in a lot easier and efficient way.
How are recursive functions stored in memory?
Recursion uses more memory, because the recursive function adds to the stack with each recursive call, and keeps the values there until the call is finished. The recursive function uses LIFO (LAST IN FIRST OUT) Structure just like the stack data structure. https://www.geeksforgeeks.org/stack-data-structure/
What is the base condition in recursion?
In the recursive program, the solution to the base case is provided and the solution to the bigger problem is expressed in terms of smaller problems.
int fact(int n)
{
if (n < = 1) // base case
return 1;
else
return n*fact(n-1);
}
In the above example, the base case for n < = 1 is defined and the larger value of a number can be solved by converting to a smaller one till the base case is reached.
How a particular problem is solved using recursion?
The idea is to represent a problem in terms of one or more smaller problems, and add one or more base conditions that stop the recursion. For example, we compute factorial n if we know the factorial of (n-1). The base case for factorial would be n = 0. We return 1 when n = 0.
Why Stack Overflow error occurs in recursion?
If the base case is not reached or not defined, then the stack overflow problem may arise. Let us take an example to understand this.
int fact(int n)
{
// wrong base case (it may cause
// stack overflow).
if (n == 100)
return 1;
else
return n*fact(n-1);
}
If fact(10) is called, it will call fact(9), fact(8), fact(7), and so on but the number will never reach 100. So, the base case is not reached. If the memory is exhausted by these functions on the stack, it will cause a stack overflow error.
What is the difference between direct and indirect recursion?
A function fun is called direct recursive if it calls the same function fun. A function fun is called indirect recursive if it calls another function say fun_new and fun_new calls fun directly or indirectly. The difference between direct and indirect recursion has been illustrated in Table 1.
// An example of direct recursion
void directRecFun()
{
// Some code....
directRecFun();
// Some code...
}
// An example of indirect recursion
void indirectRecFun1()
{
// Some code...
indirectRecFun2();
// Some code...
}
void indirectRecFun2()
{
// Some code...
indirectRecFun1();
// Some code...
}
What is the difference between tailed and non-tailed recursion?
A recursive function is tail recursive when a recursive call is the last thing executed by the function. Please refer tail recursion article for details.
How memory is allocated to different function calls in recursion?
When any function is called from main(), the memory is allocated to it on the stack. A recursive function calls itself, the memory for a called function is allocated on top of memory allocated to the calling function and a different copy of local variables is created for each function call. When the base case is reached, the function returns its value to the function by whom it is called and memory is de-allocated and the process continues.
Let us take the example of how recursion works by taking a simple function.
CPP
#include <bits/stdc++.h>
using namespace std;
void printFun(int test)
{
if (test < 1)
return;
else {
cout << test << " ";
printFun(test - 1);
cout << test << " ";
return;
}
}
int main()
{
int test = 3;
printFun(test);
}
|
Java
class GFG {
static void printFun(int test)
{
if (test < 1)
return;
else {
System.out.printf("%d ", test);
printFun(test - 1);
System.out.printf("%d ", test);
return;
}
}
public static void main(String[] args)
{
int test = 3;
printFun(test);
}
}
|
Python3
def printFun(test):
if (test < 1):
return
else:
print(test, end=" ")
printFun(test-1)
print(test, end=" ")
return
test = 3
printFun(test)
|
C#
using System;
class GFG {
static void printFun(int test)
{
if (test < 1)
return;
else {
Console.Write(test + " ");
printFun(test - 1);
Console.Write(test + " ");
return;
}
}
public static void Main(String[] args)
{
int test = 3;
printFun(test);
}
}
|
PHP
<?php
function printFun($test)
{
if ($test < 1)
return;
else
{
echo("$test ");
printFun($test-1);
echo("$test ");
return;
}
}
$test = 3;
printFun($test);
?>
|
Javascript
<script>
function printFun(test)
{
if (test < 1)
return;
else {
document.write(test + " ");
printFun(test - 1);
document.write(test + " ");
return;
}
}
let test = 3;
printFun(test);
</script>
|
Time Complexity: O(1)
Auxiliary Space: O(1)
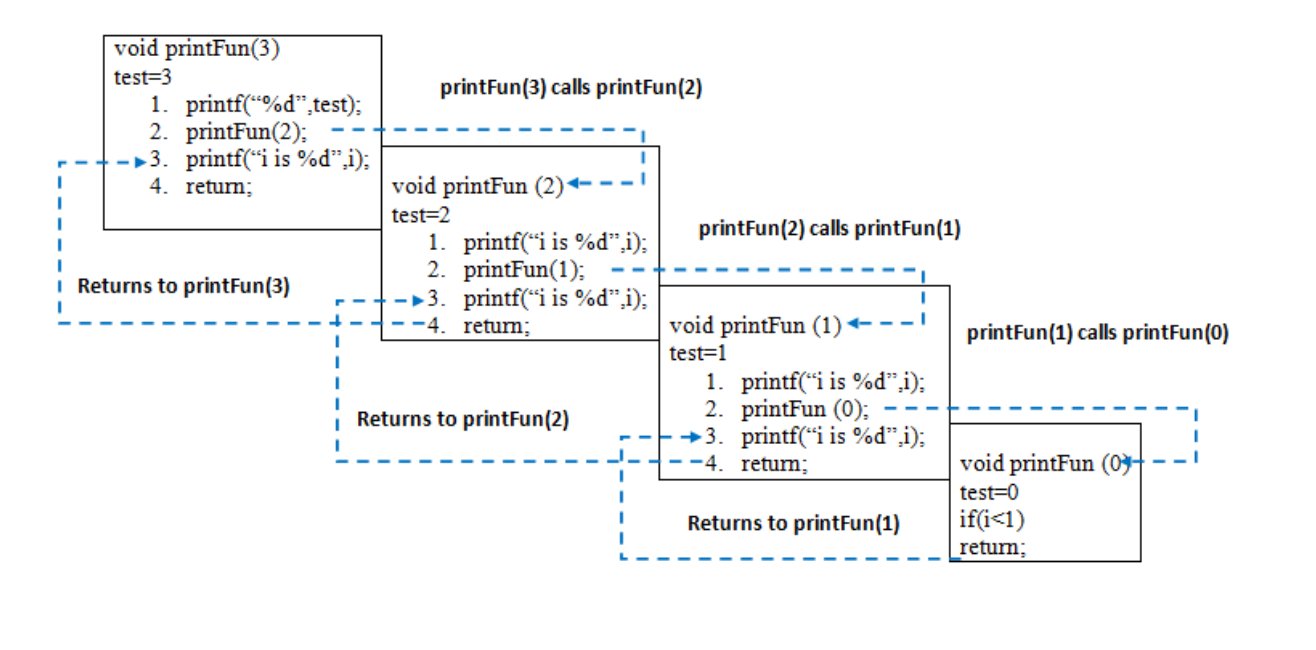
When printFun(3) is called from main(), memory is allocated to printFun(3) and a local variable test is initialized to 3 and statement 1 to 4 are pushed on the stack as shown in below diagram. It first prints ‘3’. In statement 2, printFun(2) is called and memory is allocated to printFun(2) and a local variable test is initialized to 2 and statement 1 to 4 are pushed into the stack. Similarly, printFun(2) calls printFun(1) and printFun(1) calls printFun(0). printFun(0) goes to if statement and it return to printFun(1). The remaining statements of printFun(1) are executed and it returns to printFun(2) and so on. In the output, values from 3 to 1 are printed and then 1 to 3 are printed. The memory stack has been shown in below diagram.
Recursion VS Iteration
| SR No. |
Recursion |
Iteration |
| 1) |
Terminates when the base case becomes true. |
Terminates when the condition becomes false. |
| 2) |
Used with functions. |
Used with loops. |
| 3) |
Every recursive call needs extra space in the stack memory. |
Every iteration does not require any extra space. |
| 4) |
Smaller code size. |
Larger code size. |
Now, let’s discuss a few practical problems which can be solved by using recursion and understand its basic working. For basic understanding please read the following articles.
Basic understanding of Recursion.
Problem 1: Write a program and recurrence relation to find the Fibonacci series of n where n>2 .
Mathematical Equation:
n if n == 0, n == 1;
fib(n) = fib(n-1) + fib(n-2) otherwise;
Recurrence Relation:
T(n) = T(n-1) + T(n-2) + O(1)
Recursive program:
Input: n = 5
Output:
Fibonacci series of 5 numbers is : 0 1 1 2 3
Implementation:
C++
#include <bits/stdc++.h>
using namespace std;
int fib(int n)
{
if (n == 0)
return 0;
if (n == 1 || n == 2)
return 1;
else
return (fib(n - 1) + fib(n - 2));
}
int main()
{
int n = 5;
cout<<"Fibonacci series of 5 numbers is: ";
for (int i = 0; i < n; i++)
{
cout<<fib(i)<<" ";
}
return 0;
}
|
C
#include <stdio.h>
int fib(int n)
{
if (n == 0)
return 0;
if (n == 1 || n == 2)
return 1;
else
return (fib(n - 1) + fib(n - 2));
}
int main()
{
int n = 5;
printf("Fibonacci series "
"of %d numbers is: ",
n);
for (int i = 0; i < n; i++) {
printf("%d ", fib(i));
}
return 0;
}
|
Java
import java.util.*;
class GFG
{
static int fib(int n)
{
if (n == 0)
return 0;
if (n == 1 || n == 2)
return 1;
else
return (fib(n - 1) + fib(n - 2));
}
public static void main(String []args)
{
int n = 5;
System.out.print("Fibonacci series of 5 numbers is: ");
for (int i = 0; i < n; i++)
{
System.out.print(fib(i)+" ");
}
}
}
|
Python3
def fib(n):
if (n == 0):
return 0
if (n == 1 or n == 2):
return 1
else:
return (fib(n - 1) + fib(n - 2))
n = 5;
print("Fibonacci series of 5 numbers is :",end=" ")
for i in range(0,n):
print(fib(i),end=" ")
|
C#
using System;
public class GFG
{
static int fib(int n)
{
if (n == 0)
return 0;
if (n == 1 || n == 2)
return 1;
else
return (fib(n - 1) + fib(n - 2));
}
static public void Main ()
{
int n = 5;
Console.Write("Fibonacci series of 5 numbers is: ");
for (int i = 0; i < n; i++)
{
Console.Write(fib(i) + " ");
}
}
}
|
Javascript
<script>
function fib(n)
{
if(n == 0)
return 0;
if(n == 1 || n == 2)
return 1;
else
return fib(n-1) + fib(n-2);
}
let n = 5;
document.write("Fibonacci series of 5 numbers is: ");
for(let i = 0; i < n; i++)
{
document.write(fib(i) + " ");
}
</script>
|
Output
Fibonacci series of 5 numbers is: 0 1 1 2 3
Time Complexity: O(2n)
Auxiliary Space: O(n)
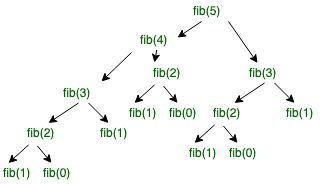
Here is the recursive tree for input 5 which shows a clear picture of how a big problem can be solved into smaller ones.
fib(n) is a Fibonacci function. The time complexity of the given program can depend on the function call.
fib(n) -> level CBT (UB) -> 2^n-1 nodes -> 2^n function call -> 2^n*O(1) -> T(n) = O(2^n)
For Best Case.
T(n) = ?(2^n\2)
Working:
Problem 2: Write a program and recurrence relation to find the Factorial of n where n>2 .
Mathematical Equation:
1 if n == 0 or n == 1;
f(n) = n*f(n-1) if n> 1;
Recurrence Relation:
T(n) = 1 for n = 0
T(n) = 1 + T(n-1) for n > 0
Recursive Program:
Input: n = 5
Output:
factorial of 5 is: 120
Implementation:
C++
#include <bits/stdc++.h>
using namespace std;
int f(int n)
{
if (n == 0 || n == 1)
return 1;
else
return n * f(n - 1);
}
int main()
{
int n = 5;
cout<<"factorial of "<<n<<" is: "<<f(n);
return 0;
}
|
C
#include <stdio.h>
int f(int n)
{
if (n == 0 || n == 1)
return 1;
else
return n * f(n - 1);
}
int main()
{
int n = 5;
printf("factorial of %d is: %d", n, f(n));
return 0;
}
|
Java
public class GFG
{
static int f(int n)
{
if (n == 0 || n == 1)
return 1;
else
return n * f(n - 1);
}
public static void main(String[] args)
{
int n = 5;
System.out.println("factorial of " + n + " is: " + f(n));
}
}
|
Python3
def f(n):
if (n == 0 or n == 1):
return 1;
else:
return n * f(n - 1);
if __name__=='__main__':
n = 5;
print("factorial of",n,"is:",f(n))
|
C#
using System;
class GFG {
static int f(int n)
{
if (n == 0 || n == 1)
return 1;
else
return n * f(n - 1);
}
static void Main()
{
int n = 5;
Console.WriteLine("factorial of " + n + " is: " + f(n));
}
}
|
Javascript
<script>
function f(n)
{
if(n == 0 || n == 1)
return 1;
else
return n*f(n-1);
}
let n = 5;
document.write("factorial of "+ n +" is: " + f(n));
</script>
|
Output
factorial of 5 is: 120
Time complexity: O(n)
Auxiliary Space: O(n)
Working:

Diagram of factorial Recursion function for user input 5.
Example: Real Applications of Recursion in real problems
Recursion is a powerful technique that has many applications in computer science and programming. Here are some of the common applications of recursion:
- Tree and graph traversal: Recursion is frequently used for traversing and searching data structures such as trees and graphs. Recursive algorithms can be used to explore all the nodes or vertices of a tree or graph in a systematic way.
- Sorting algorithms: Recursive algorithms are also used in sorting algorithms such as quicksort and merge sort. These algorithms use recursion to divide the data into smaller subarrays or sublists, sort them, and then merge them back together.
- Divide-and-conquer algorithms: Many algorithms that use a divide-and-conquer approach, such as the binary search algorithm, use recursion to break down the problem into smaller subproblems.
- Fractal generation: Fractal shapes and patterns can be generated using recursive algorithms. For example, the Mandelbrot set is generated by repeatedly applying a recursive formula to complex numbers.
- Backtracking algorithms: Backtracking algorithms are used to solve problems that involve making a sequence of decisions, where each decision depends on the previous ones. These algorithms can be implemented using recursion to explore all possible paths and backtrack when a solution is not found.
- Memoization: Memoization is a technique that involves storing the results of expensive function calls and returning the cached result when the same inputs occur again. Memoization can be implemented using recursive functions to compute and cache the results of subproblems.
These are just a few examples of the many applications of recursion in computer science and programming. Recursion is a versatile and powerful tool that can be used to solve many different types of problems.
Explanation: one real example of recursion:
Recursion is a programming technique that involves a function calling itself. It can be a powerful tool for solving complex problems, but it also requires careful implementation to avoid infinite loops and stack overflows.
Here’s an example of implementing recursion in Python:
C++
#include <iostream>
using namespace std;
int factorial(int n)
{
if (n == 0 || n == 1) {
return 1;
}
else {
return n * factorial(n - 1);
}
}
int main()
{
int result = factorial(5);
cout << result <<endl;
return 0;
}
|
Java
import java.util.*;
class Main {
public static int factorial(int n)
{
if (n == 0 || n == 1) {
return 1;
}
else {
return n * factorial(n - 1);
}
}
public static void main(String[] args)
{
int result = factorial(5);
System.out.println(result);
}
}
|
Python3
def factorial(n):
if n == 0 or n == 1:
return 1
else:
return n * factorial(n-1)
result = factorial(5)
print(result)
|
C#
using System;
class MainClass {
public static int factorial(int n)
{
if (n == 0 || n == 1) {
return 1;
}
else {
return n * factorial(n - 1);
}
}
public static void Main (string[] args) {
int result = factorial(5);
Console.WriteLine(result);
}
}
|
Javascript
function factorial(n) {
if (n === 0 || n === 1) {
return 1;
}
else {
return n * factorial(n - 1);
}
}
const result = factorial(5);
console.log(result);
|
In this example, we define a function called factorial that takes an integer n as input. The function uses recursion to compute the factorial of n (i.e., the product of all positive integers up to n).
The factorial function first checks if n is 0 or 1, which are the base cases. If n is 0 or 1, the function returns 1, since 0! and 1! are both 1.
If n is greater than 1, the function enters the recursive case. It calls itself with n-1 as the argument and multiplies the result by n. This computes n! by recursively computing (n-1)!.
It’s important to note that recursion can be inefficient and lead to stack overflows if not used carefully. Each function call adds a new frame to the call stack, which can cause the stack to grow too large if the recursion is too deep. In addition, recursion can make the code more difficult to understand and debug, since it requires thinking about multiple levels of function calls.
However, recursion can also be a powerful tool for solving complex problems, particularly those that involve breaking a problem down into smaller subproblems. When used correctly, recursion can make the code more elegant and easier to read.
What are the disadvantages of recursive programming over iterative programming?
Note that both recursive and iterative programs have the same problem-solving powers, i.e., every recursive program can be written iteratively and vice versa is also true. The recursive program has greater space requirements than the iterative program as all functions will remain in the stack until the base case is reached. It also has greater time requirements because of function calls and returns overhead.
Moreover, due to the smaller length of code, the codes are difficult to understand and hence extra care has to be practiced while writing the code. The computer may run out of memory if the recursive calls are not properly checked.
What are the advantages of recursive programming over iterative programming?
Recursion provides a clean and simple way to write code. Some problems are inherently recursive like tree traversals, Tower of Hanoi, etc. For such problems, it is preferred to write recursive code. We can write such codes also iteratively with the help of a stack data structure. For example refer Inorder Tree Traversal without Recursion, Iterative Tower of Hanoi.
Summary of Recursion:
- There are two types of cases in recursion i.e. recursive case and a base case.
- The base case is used to terminate the recursive function when the case turns out to be true.
- Each recursive call makes a new copy of that method in the stack memory.
- Infinite recursion may lead to running out of stack memory.
- Examples of Recursive algorithms: Merge Sort, Quick Sort, Tower of Hanoi, Fibonacci Series, Factorial Problem, etc.
Output based practice problems for beginners:
Practice Questions for Recursion | Set 1
Practice Questions for Recursion | Set 2
Practice Questions for Recursion | Set 3
Practice Questions for Recursion | Set 4
Practice Questions for Recursion | Set 5
Practice Questions for Recursion | Set 6
Practice Questions for Recursion | Set 7
Quiz on Recursion
Coding Practice on Recursion:
All Articles on Recursion
Recursive Practice Problems with Solutions
Share your thoughts in the comments
Please Login to comment...