Methods of Integration

Last Updated : 28 Sep, 2023

Methods of Integration in Calculus refer to the various techniques that are used to simplify the given function so that it can be integrated easily. Many times it is not possible to directly integrate a function, so we need to use a specific technique to reduce the integral analytically and then perform integration. Any method of integration involves identifying the type of integral and then deciding which method to use.

Calculus is one of the main pillars of advanced mathematics and Integration is the most important topic if you want to study calculus properly. So, Methods of integration are very important to learn so that students can solve any integration-related problems by any one of these methods.

In this article, we will study what is Integration in calculus, methods of integration mainly the method of substitution, Integration by parts, and Integration using Trigonometric Identities.

Table of Content

What is Integration in Calculus?
What are Methods of Integration?
Integration by Parts
Integration By Substitution
Integration using Trigonometric Identities
Integration by Partial Fraction
Integration of Some Special Functions
Important Points related to Methods of Integration

What is Integration in Calculus?

Integration can be defined as the summation of values when the number of terms tends to infinity. It is used to unite a part of the whole. Integration is just the reverse of differentiation and has various applications in all spheres such as physics, chemistry, space, engineering, etc.

Integration of a function or a curve can be used to find useful information such as the area under the curve or volume of the curve, etc. Integration may be of 2 types which are Definite and Indefinite Integration depending upon whether the limits of integration are mentioned or not. There are various methods to integrate a given function which are discussed below.

Related Resources,

Area Between Two Curves
Area Under the Curve

What are Methods of Integration?

We know that integration is represented using the symbol 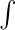$\int$ over a function f(x) as follows:

∫f(x)dx

Various methods of integration are as follows:

Integration by Parts
Integration by Substitution
Integration Using Trigonometric Identities
Integration by Partial Fraction
Integration of Some Special functions

Integration by Parts

This method is used in cases where the function to be integrated is a product of two or more functions. Let f(x) = g(x)h(x), then f(x) can be integrated by parts by using the below formula:

∫g(x).h(x).dx = g(x).∫h(x).dx – ∫(g′(x).∫h(x).dx).dx

The sequence of h(x) and g(x) should be decided using the ILATE rule which tells the priority of functions and stands for Inverse trigonometric, logarithmic, algebraic, trigonometric, and exponential functions. This means that inverse trigonometric function should be written before logarithmic, logarithmic should be written before algebraic and so on.

Read more about Integration by Parts.

Example of Integration by Parts

Example: Solve 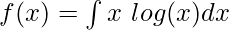$f(x) = \int x~log(x) dx$

Solution:

Given 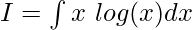$I = \int x~log(x) dx$

From ILATE rule, we know that logarithmic function has higher priority than algebraic function. Hence,

$I = \int log(x)~x~ dx$

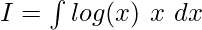
Using integration by parts,

$I = log(x)\int xdx - \int (\frac{d}{dx}(log~x)\int x~dx)dx \\ I = \frac{x^2log(x)}{2}-\int (\frac{1}{x}\times \frac{x^2}{2})dx \\ I = \frac{x^2log(x)}{2}-\int \frac{1}{2}(x)dx \\ I = \frac{x^2log(x)}{2}-\frac{x^2}{4} + c$

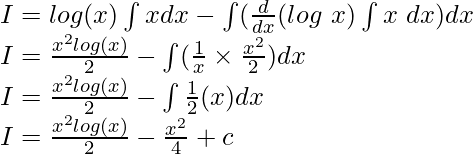
Integration By Substitution

This method is used when we find it difficult to integrate a function as it is. In this method, a certain term in the function is substituted as a new variable and the whole function is changed to a new function of a new variable. This means that:

$\int f(x)dx = \int f(u)du$

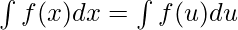
Read more about Integration By Substitution.

Example of Integration by Substitution

Let us understand it with an example.

Example: Solve 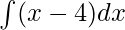$\int (x-4) dx$

Solution:

Given 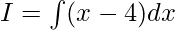$I = \int (x-4) dx$

Substitute (x-4) = u

Differentiate both sides w.r.t x to get

dx = du

Thus 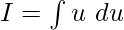$I = \int u~du$

$I = \frac{u^2}{2} + c$

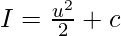
Again putting u = (x-4)

$I = \frac{(x-4)^2}{2}+c$

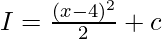
Integration using Trigonometric Identities

This method involves integrating the given function by transforming it using trigonometric identities. The value of the given function is substituted using some other function that is derived by using trigonometric identities. To know more about trigonometric identities, please refer to Trigonometric Identities.

Example of Integration using Trigonometric Identities

Let us understand this method with an example.

Example: Solve 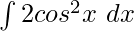$\int 2cos^2x~dx$

Solution:

Given 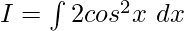$I = \int 2cos^2x~dx$

We know that cos(2x) = 2cos²x -1

2cos²x = cos(2x)+1

Substituting the value of 2cos²x, we get

$I = \int [cos(2x)-1]dx \\ I = \frac{sin(2x)}{2} - x + c$

Integration by Partial Fraction

If the function to be integrated is of the form f(x) = g(x)/h(x) where g(x) and h(x) are polynomials, then we use the method of partial fraction. There are multiple cases in partial fractions depending upon the type of f(x).

Type of function f(x)	Partial Fraction
$\frac{px+q}{(x-a)(x-b)}$ where a ≠ b	$\frac{A}{x-a}+\frac{B}{x-b}$
$\frac{px+q}{(x-a)^2}$	$\frac{A}{x-a}+\frac{B}{(x-a)^2}$
$\frac{px^2+qx+r}{(x-a)(x-b)(x-c)}$	$\frac{A}{x-a} + \frac{B}{x-b}+ \frac{C}{x-c}$
$\frac{px^2+qx+r}{(x-a)^2(x-b)}$	$\frac{A}{x-a} + \frac{B}{(x-a)^2}+ \frac{C}{x-b}$
$\frac{px^2+qx+r}{(x-a)(x^2+bx+c)}$	$\frac{A}{x-a} + \frac{Bx+c}{x^2+bx+c}$

In all these cases, we need to take the LCM of the partial fractions to make the denominator the same. After that, we compare the numerator on the LHS and RHS. Then substitute the suitable value of x in order to make any one part of the numerator zero and determine the value of A, B and C.

Read more about Integration by Partial Fraction.

Example of Integration by Partial Fraction

Let us understand partial fractions with an example.

Example: Integrate the function f(x) = x/(x-2)(x+3).

Given f(x) = x/(x-2)(x+3)

It is of the form 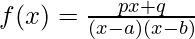$f(x) = \frac{px+q}{(x-a)(x-b)}$

So it can be written as 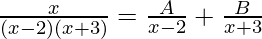$\frac{x}{(x-2)(x+3)} = \frac{A}{x-2}+\frac{B}{x+3}$

Taking LCM on RHS, we get,

$\frac{x}{(x-2)(x+3)} = \frac{A(x+3)+B(x-2)}{(x-2)(x+3)}$

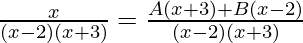
Comparing numerators on LHS and RHS:

$x = A(x+3)+B(x-2)$

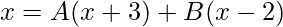
Put x = 2 to get,

2 = 5A or A = 2/5

similarly put x = -3 to get

-3 = -5B or B = 3/5

Thus 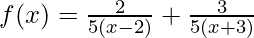$f(x) = \frac{2}{5(x-2)}+ \frac{3}{5(x+3)}$

$\int f(x) = \int[\frac{2}{5(x-2)}+ \frac{3}{5(x+3)}]dx\\ = \frac{2}{5}\int\frac{1}{x-2} + \frac{3}{5}\int\frac{1}{x+3}\\ = \frac{2}{5}\log{(x-2)} + \frac{3}{5}\log(x+3)$

Integration of Some Special Functions

In Mathematics, we have some special functions which have pre-defined integration formulas. These functions and their integration are shown below:

$\int \frac{dx}{ (x^2 - a^2)} = \frac{a}{2}log | \frac{x - a} {x + a} | + c$
$\int \frac{dx}{ (a^2 - x^2)} = \frac{a}{2}log | \frac{a + x} {a - x} | + c$
$\int \frac{dx} {x^2 + a^2} = \frac{tan^{-1}\frac{x}{a}}{a} + c$
$\int \frac{ dx} {√ (x^2 - a^2)} = log| x+√(x^2 - a^2) | + c$
$\frac{ dx} {√ (a^2 - x^2)} = sin^{-1} (xa) + c$
$\int \frac{dx} {√ (x^2 + a^2)} = log | x + √(x^2 + a^2) | + c$

Related Resources,

Integrals
Integration Formulas
Differentaition and Integration

1. Fundamental Theorem of Calculus: This theorem states that the definite integral of a function can be evaluated by finding an antiderivative of the function and subtracting the values at the endpoints of the interval. It connects integration with differentiation.

2. Indefinite Integrals: These are also known as antiderivatives. Finding an indefinite integral involves finding a function whose derivative is the given function. Common techniques include power rule, exponential rule, and trigonometric rules.

3. Integration by Substitution: This technique involves making a substitution to simplify an integral. The substitution is chosen to make the integral more manageable, often by letting a variable equal part of the integrand.

4. Integration by Parts: This method is used to integrate the product of two functions. It is derived from the product rule for differentiation and involves choosing parts of the integrand to differentiate and integrate.

5. Trigonometric Integrals: Special integrals involving trigonometric functions often require trigonometric identities or substitutions. Examples include integrals of sin(x), cos(x), sec(x), and csc(x) functions.

6. Partial Fractions: When integrating rational functions (ratios of polynomials), you can use partial fraction decomposition to break down the integrand into simpler fractions. This facilitates integration.

Solved Examples on Methods of Integration

Example 1: Solve 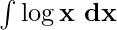$\bold{\int \log x~dx}$ .

Solution:

Given I = \int \log x~dx = \int \log x.1~dx

The functions are already written according to ILATE rule. Using integration by parts we get,

$I = \log x\int1dx - \int(\frac{d}{dx}(\log x)\int1dx)dx \\ I = x\log x - \int\frac{1}{x}.x~dx \\ I = x\log x - \int1dx \\ I = x\log x - x + c$

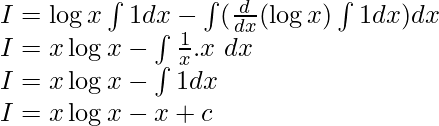
Example 2: Solve 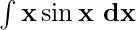$\bold{\int x \sin x~dx}$

Solution:

Given I = \int x \sin x~dx

The functions are already written according to ILATE rule. Using integration by parts we get,

$I = x\int \sin xdx - \int(\frac{d}{dx}x\int\sin x)dx \\ I = -x\cos x- \int-\cos x~dx \\ I = -x \cos x + \int\cos xdx \\ I = -x \cos x + \sin x + c$

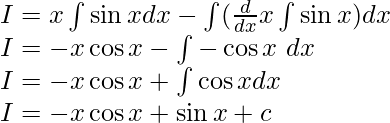
Example 3: Solve 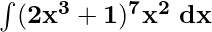$\bold{\int (2x^3+1)^7x^2~dx}$

Solution:

Given 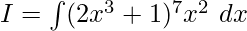$I = \int (2x^3+1)^7x^2~dx$

Substitute (2x³+1) = u

Differentiate both sides w.r.t x to get

6x² dx = du

x²dx = du/6

Rewriting the given function as 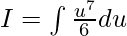$I = \int \frac{u^7}{6}du$

$I = \frac{1}{6}(\frac{u^8}{8}) + c \\ I = \frac{u^8}{48} + c \\ I = \frac{(2x^3+1)^8}{48}+c$

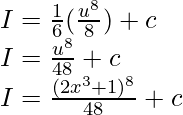
Example 4: Solve 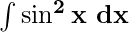$\bold{\int \sin^2x ~dx}$

Solution:

Given 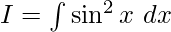$I = \int \sin^2x ~dx$

We know that cos(2x) = 1 – 2sin²x

(1-cos2x)/2 = sin²x

Substituting the value of sin²x, we get

$I = \int \frac{(1-\cos(2x))}{2}dx \\ I = \frac{1}{2}[x-\frac{\sin(2x)}{2}] + c \\ I = \frac{x}{2}-\frac{\sin(2x)}{4}+c$

Example 5: Solve 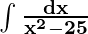$\bold{\int \frac{dx}{x^2-25}}$ .

Solution:

Given

$I = \int \frac{dx}{x^2-25} = \int \frac{dx}{x^2-5^2}$

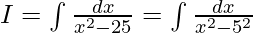
Using

$\int \frac{dx}{ (x^2 - a^2)} = \frac{a}{2}log | \frac{x - a} {x + a} | + c \\ I = \frac{5}{2}log | \frac{x - 5} {x + 5} | + c$

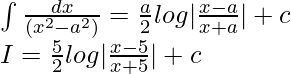
Practice Problems on Methods of Integration

Problem 1: Calculate the following integrals:

∫(3x² + 2x – 5) dx
∫(e^x + 1) dx
∫(sin(x) + cos(x)) dx

Problem 2: Use the substitution method to evaluate the following integrals:

∫(2x + 1)³ dx
∫(x² + 4x + 3)√(x³ + 6x² + 9x) dx
∫2x cos(x²) dx

Problem 3: Apply integration by parts to solve the following integrals:

∫x ln(x) dx
∫x² sin(x) dx
∫e^x cos(x) dx

Problem 4: Use partial fraction decomposition to integrate:

∫(3x² + 2)/(x³ + 4x² + 4x) dx
∫(x³ – 2x² + 5x – 1)/(x² – 3x + 2) dx
∫(4x³ – 2x² + 3)/(x⁴ + 2x² + 1) dx

FAQs on Methods of Integration

1. What do you mean by integration?

Integration can be defined as the summation of values when the number of terms tend to infinity. It is used to unite a part of whole. Integration is just the reverse of differentiation.

2. What are the five methods of integration?

Various methods of integration are as follows:

Integration by Parts
Integration by Substitution
Integration Using Trigonometric Identities
Integration of Some special functions

3. What is the Best Integration Method?

There is no such method which can be said the best method of integration, as the best integration method depends on the specific problem and context.

4. What is the Special Method of Integration?

Integration by parts is considered as special method of integration as it is used to find the integral of the product of two functions.

5. What is the Formula to Integrate a Function by Parts?

Let f(x) = g(x)h(x), then f(x) can be integrated by parts by using the below formula:

∫g(x).h(x).dx = g(x).∫h(x).dx – ∫(g′(x).∫h(x).dx).dx

6. Which Rule is followed to Decide the Order of Functions when Integrating by Parts?

ILATE rule is used to decide the order of functions when integrating by parts. It stands for Inverse trigonometric, logarithmic, algebraic, trigonometric, and exponential function and this is the order for the fucntions.

7. Why do We Use Methods of Integration?

Methods of integration are used to simplify the integral expressions which are complex and perform their integration easily by making them simpler.

8. What are the Two Types of Integration?

Definite integration and indefinite integration are two types of integration.

9. What is the Partial Fraction Decomposition when f(x) is of the Form 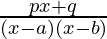$\frac{px+q}{(x-a)(x-b)}$ ?

In this case, partial fraction will be of the form 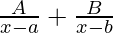$\frac{A}{x-a}+\frac{B}{x-b}$

10. What is the Reverse Chain Rule?

Reverse chain rule is the method to integrate some functions which are given as f(g(x))g'(x). This is the same as the integration by substitution.

Suggest improvement

Limit of Integration

Share your thoughts in the comments

Methods of Integration

What is Integration in Calculus?

What are Methods of Integration?

Integration by Parts

Example of Integration by Parts

Integration By Substitution

Example of Integration by Substitution

Integration using Trigonometric Identities

Example of Integration using Trigonometric Identities

Integration by Partial Fraction

Example of Integration by Partial Fraction

Integration of Some Special Functions

Important Points related to Methods of Integration

Solved Examples on Methods of Integration

Practice Problems on Methods of Integration

FAQs on Methods of Integration

1. What do you mean by integration?

2. What are the five methods of integration?

3. What is the Best Integration Method?

4. What is the Special Method of Integration?

5. What is the Formula to Integrate a Function by Parts?

6. Which Rule is followed to Decide the Order of Functions when Integrating by Parts?

7. Why do We Use Methods of Integration?

8. What are the Two Types of Integration?

9. What is the Partial Fraction Decomposition when f(x) is of the Form ?

10. What is the Reverse Chain Rule?

Please Login to comment...

Similar Reads

What kind of Experience do you want to share?

9. What is the Partial Fraction Decomposition when f(x) is of the Form $\frac{px+q}{(x-a)(x-b)}$ ?