Integration is the important part of the calculus. The integration is the method of finding the anti-derivative of any function. The integration is applied to the integrals. Integration has many applications in different fields like mathematics, physics, engineering and many more.
This article collects all the in-depth knowledge about integration in one place including all the formulas of integration and how to find integrals. It also explores the properties and applications of integration with its solved examples. Let’s start exploring the topic of Integration.
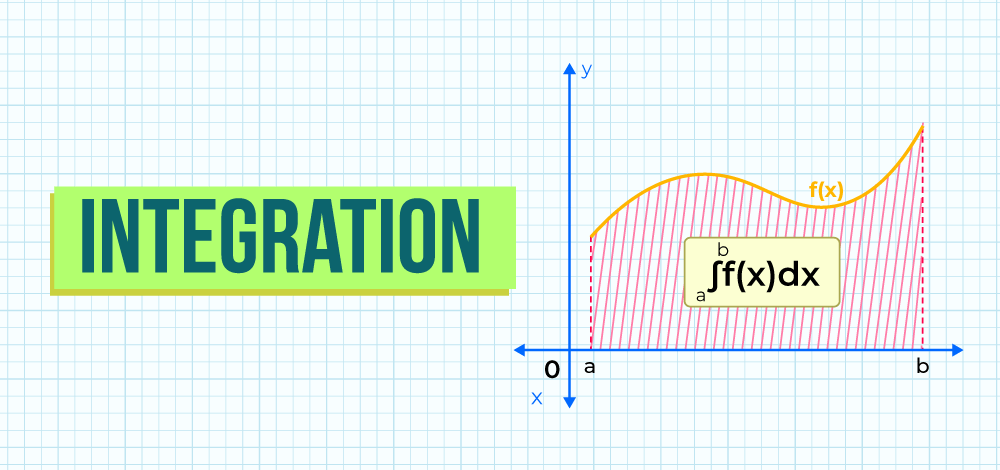
What is Integration?
The process of determining the function from its derivative is called Integration. In other words, the procedure of finding the anti-derivatives of the function is called the integration. The result obtained after the integration is called integral. The integration can be done using multiple methods like integration by substitution, integration by parts, integration by partial fraction, etc.
Integration Definition
If f is the positive continuous function defined over an interval [a, b] then, the area between the function f graph and x-axis results in the integration of f w.r.t x. The area under the curve gives the definite integration of f.
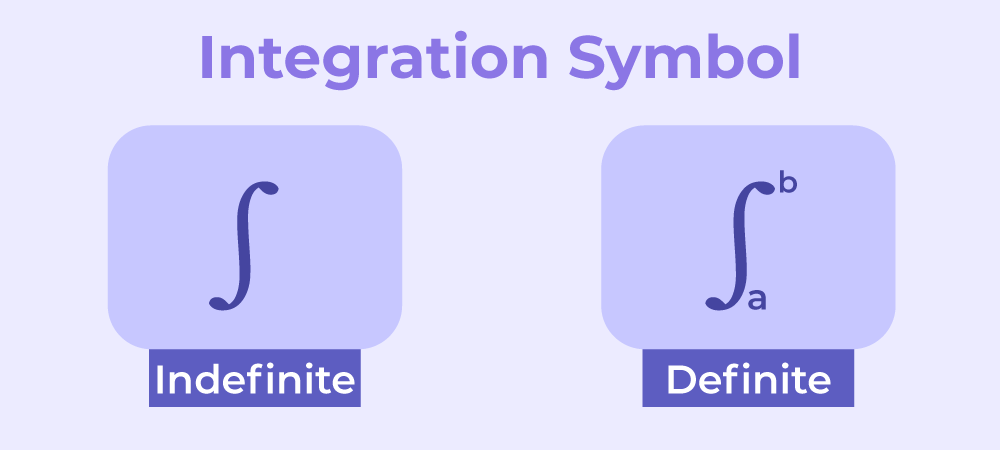
Integration Symbol
The symbol of integration is ∫. For the definite integral we apply limits and use symbol ∫ab .
Rules for Integration
Some important rules of integration are:
- Power Rule
- Addition Rule
- Subtraction Rule
- Constant Multiple Rule
Power Rule of Integration
The power rule of integration is stated as:
∫xn dx = xn+1/ (n + 1)
Addition Rule of Integration
The addition rule of integration is stated as:
∫{f(x) + g(x)} dx = ∫f(x) dx + ∫g(x) dx
Subtraction Rule of Integration
The subtraction rule of integration is stated as:
∫{f(x) – g(x)} dx = ∫f(x) dx – ∫g(x) dx
Constant Multiple Rule of Integration
The multiplication of constant rule of integration can be stated as:
∫k f(x) dx = k ∫f(x) dx,
Where k is constant.
Antiderivative: Integration as Inverse Process of Differentiation
The process of finding the antiderivative i.e., the inverse of the derivative is called integration. If Φ(x) is a function and the derivative of Φ(x) is f(x) then, integration of f(x) results in Φ(x).
(d / dx) {Φ(x)} = f(x) ⇔ ∫f(x) dx = Φ(x) + C
OR
∫[d/dx]g(x) dx = g(x)
The various integration formulas are:
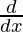 {Φ(x)} = f(x) ⇔ ∫f(x) dx = Φ(x) + C
{Φ(x)} = f(x) ⇔ ∫f(x) dx = Φ(x) + C- ∫xn dx = xn+1/ (n + 1) + C
- ∫(1 / x) dx = loge|x| + C
- ∫ex dx = ex + C
- ∫ax dx = [ax/ logea] + C
- ∫sin x dx = -cos x + C
- ∫cos x dx = sin x + C
- ∫sec2x dx = tan x + C
- ∫cosec2x dx = -cot x + C
- ∫sec x tan x dx = sec x + C
- ∫cosec x cot x dx = – cosec x + C
- ∫tan x dx = ln |sec x| + C = -ln |cos x| + C
- ∫cot x dx = ln |sin x| + C
- ∫sec x dx = ln |sec x + tan x| + C
- ∫cosec x dx = ln |cosec x – cot x| + C
- ∫
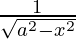 dx = sin-1(x/a) +C
dx = sin-1(x/a) +C - ∫-
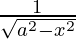 dx = cos-1(x/a) + C
dx = cos-1(x/a) + C - ∫
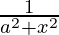 dx = (1/a) tan-1 (x/a) + C
dx = (1/a) tan-1 (x/a) + C - ∫-
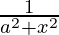 dx = (1/a) cot-1(x/a) + C
dx = (1/a) cot-1(x/a) + C - ∫
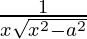 dx = (1/a) sec-1(x/a) + C
dx = (1/a) sec-1(x/a) + C - ∫-
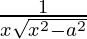 dx = (1/a)cosec-1(x/a) + C
dx = (1/a)cosec-1(x/a) + C
Learn more about Integration Formulas.
Types of Integration
Integration can be classified into three types:
- Definite Integration
- Indefinite Integration
- Improper Integration
Definite Integration
The integration with limits is called as the definite integration. The antiderivative p(x) of a continuous function f(x) on the interval [a, b] is known as definite integration. It is represented by and its value equals to p(b) – p(a) where p(b) is antiderivative at x = b and p(a) is the antiderivative at x = a. The a and b are called the limits of integration where a is the lower limit and b is the upper limit of integration. The interval [a, b] is called the interval of the integration. In the definite integration, the constant of integration is not required.
Learn more about Definite Integration.
Indefinite Integration
The integration with no limits is called the indefinite integration. In the indefinite integration, we add a constant with the result called the constant of integration. The integration of f(x) is given by:
∫f(x) dx = P(x) + C
Where,
- x is the variable of integration,
- f(x) is integrand,
- P(x) is antiderivative of f(x), and
- C is constant of Integration.
Read more about Indefinite Integration.
Improper Integration
The integration whose integrand is not bounded, or the limit of the integral is infinity, then the integration is called as improper integration. Some examples of improper integrations are: 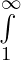 f(x)dx or
f(x)dx or 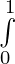 (dx / x)
(dx / x)
Integration Techniques
There are various methods to find the integration of a function. Some of these are listed below:
Read more about Method of Integration.
Integration of Basic Functions
There are different integration formulas for different functions. Below we will discuss the integration of different functions in depth and get complete knowledge about the integration formulas.
Integration of Constant Function
The integration of a constant function is given by:
∫k dx = kx + C, where k is constant
Integration of Trigonometric Functions
The integration of trigonometric functions is given by:
- ∫sin x dx = -cos x + C
- ∫cos x dx = sin x + C
- ∫sec2x dx = tan x + C
- ∫cosec2x dx = -cot x + C
- ∫sec x tan x dx = sec x + C
- ∫cosec x cot x dx = – cosec x + C
- ∫tan x dx = -log |cos x| + C
- ∫cot x dx = log |sin x| + C
- ∫sec x dx = log |sec x + tan x| + C
- ∫cosec x dx = log |cosec x – cot x| + C
Integration of Exponential and Logarithmic Functions
The integration of exponential and logarithmic function is given by:
- ∫(1 / x) dx = loge|x| + C
- ∫ex dx = ex + C
- ∫ax dx = [ax/ logea] + C
Applications of Integration
There are various applications of integration. Some of them are listed below:
- Integration is used to find area under the curve.
- It is also used to find the volumes.
- Integration is used to find area between the two curves.
- It is used in multiple formulas in physics.
Integration in Physics and Engineering
Integration is used widely in Physics and Engineering.
- In Physics integration is used in multiple formulas for example finding the velocity from acceleration and many more.
- In Engineering integration is used in different fields and in many formulas of engineering mechanics etc.
Integration in Economics and Finance
Integration is also helpful in Economics and Finance to calculate marginal and total revenue, costs, profits, consumer and producer surplus, capital accumulation over a specified time and in the Lorenz curve and Gini coefficient.
Integration vs Differentiation
The basic difference between integration and differentiation is tabulated below:
|
| Definition | Finding the rate of change or slope of a function at a point. | Finding the continuous sum or the area under a curve. |
| Operation | Derivative of a function f(x) is denoted as f'(x) or dy/dx. | Integral of a function f(x) is denoted as ∫f(x) dx. |
| Notation | d/dx or ∂/∂x (Leibniz notation), f'(x) (Prime notation). | ∫ (Integral symbol), ∫f(x) dx (Indefinite integral), ∫[a, b]f(x) dx (Definite integral). |
| Reverse Operation | The antiderivative of a function f'(x) is F(x) + C, where F(x) is an antiderivative of f(x) and C is the constant of integration. | Finding the derivative of a function F(x) yields f(x), but there may be a constant of integration (C) when ∫f(x) dx. |
| Geometric Interpretation | Derivative represents the slope of the tangent line to the curve at a point. | Integral represents the area between the curve and the x-axis over a given interval. |
| Applications | Used to analyze motion, optimization, and rates of change in various real-world problems. | Used for finding accumulated quantities such as area, volume, work, and other totals. |
| Linearity | Follows the linearity property: d/dx [af(x) + bg(x)] = af'(x) + bg'(x) | Follows the linearity property: ∫[af(x) + bg(x)] dx = a∫f(x) dx + b∫g(x) dx |
| Product Rule | Utilizes the product rule for differentiation: (uv)’ = u’v + uv’ | Utilizes integration by parts for integration: ∫u dv = uv – ∫v du |
| Chain Rule | Utilizes the chain rule for differentiation: (f(g(x)))’ = f'(g(x)) * g'(x) | No direct analogue in integration, but there is a technique called substitution. |
| Fundamental Theorem | Fundamental Theorem of Calculus relates differentiation and integration: ∫[a, b]f'(x) dx = f(b) – f(a). | Fundamental Theorem of Calculus states that ∫[a, b]f(x) dx can be evaluated by finding an antiderivative F(x) of f(x) and applying it at the limits: F(b) – F(a). |
Read More,
Solved Examples on Integration
Example 1: Solve: ∫x6dx
Solution:
∫xn dx = xn+1/ (n + 1) + C
∫x6 dx = x6+1/ (6 + 1) + C
∫x6 dx = [x7/ 7] + C
Example 2: Solve: ∫3x+2dx
Solution:
∫3x+2dx = ∫3x+2dx
∫3x+2dx = ∫3x.32dx
∫3x+2dx = 9 ∫3xdx
∫3x+2dx = 9[3x / loge3] + C
Example 3: Solve: ∫(x3 + 4x2 + 3x + 1)dx
Solution:
∫(x3 + 4x2 + 3x + 1)dx = ∫x3 dx + ∫(4x2) dx + ∫(3x) dx + ∫(1) dx
∫(x3 + 4x2 + 3x + 1)dx = [x3+1 / (3 + 1)] + 4 [x2+1 / (2 + 1)] + 3[x1+1 / (1 + 1)] + x + C
∫(x3 + 4x2 + 3x + 1)dx = [x4 / 4] + 4 [x3 / 3] + 3[x2 / 2] + x + C
Example 4: Solve: ∫(x + 3sinx)dx
Solution:
∫(x + 3sinx) dx = ∫x dx + ∫ (3sinx) dx
∫(x + 3sinx) dx = [x1+1 / (1 +1)] + 3(-cos x) + C
∫(x + 3sinx) dx = (x2 / 2) – 3 cos x + C
Example 5: Solve: ∫[1/ (x2 + 25)] dx
Solution:
∫[1/ (x2 + 25)] dx = ∫[1/ (x2 + 52)] dx
∫[1/ (x2 + 25)] dx = (1 / 5) tan-1 (x / 5) + C
Example 6: Solve: ∫(2ex + x3) dx
Solution:
∫(2ex + x3) dx = ∫2ex dx + ∫x3 dx
∫(2ex + x3) dx = 2ex + [x3+1 /(3 +1)] + C
∫(2ex + x3) dx = 2ex + [x4 /4] + C
Practice Questions on Integration
Question 1: Evaluate: ∫ (x4 + ex + 3sinx) dx
Question 2: Calculate: ∫sin x. cos x dx
Question 3: Simplify: ∫1 / {8 √(x2 – 64)} dx
Question 4: Calculate: ∫(sin x – cos x) / (sinx + cos x) dx
Question 5: Evaluate: ∫ tan 5x dx
Question 6: Simplify: ∫ [1 / (x2 + 2)] dx
Integration – FAQs
1. What does Integration mean?
The process of finding the anti-derivative of the function is called the integration.
2. What is an Integral in Math?
An integral in math is a concept used to find the area under a curve or the sum of quantities over an interval.
3. What is the Notation of Integration?
The notation of the integration is ∫.
4. What is the Fundamental Theorem of Calculus?
The Fundamental Theorem of Calculus states that the integral of a function’s derivative over an interval is equal to the difference in the function’s values at the interval’s endpoints.
5. How to Evaluate Integration of Function?
To evaluate the integration of a function, we can use integration formulas, Integration by substitution, Integration by parts, and Integration by partial fraction.
6. What is the Difference Between Definite and Indefinite Integrals?
A definite integral computes the exact numerical value of the quantity between specified limits, whereas an indefinite integral, represents a family of functions related to the original function without specific limits.
7. What are Some Applications of Integration in Real Life?
Some applications of integration are finding area of the curve, finding the area between two curves and volumes etc.
8. What is Integral and Its Types?
Integral is also known as continuous summation as it is defined as the limit of discrete summation when the limit of parameter approaches infinite. There are three types of integrals: Indefinite, Definite and Improper Integral.
9. What are Improper Integrals?
Improper integrals are integrals where one or both of the integration limits are infinite, or the integrand has a singularity within the interval.
10. What are the Different Methods to find Integration?
The different methods to find integration are:
- Integration by Substitution
- Integration by Parts
- Integration by Partial Fraction
11. What is Integration by Substitution?
Integration by substitution is a method in calculus to simplify the integration of complex functions by replacing variables with new ones, making the integral easy to calculate.
12. What is Integration by Parts?
Integration by parts is a technique in calculus for finding the integral of a product of two functions. It involves using a formula derived from the product rule for differentiation.
13. What is Integration by Partial Fraction?
Integration by partial fractions is a technique in calculus used to decompose a rational function into simpler fractions, making it easier to integrate each term separately.
Share your thoughts in the comments
Please Login to comment...