If you’re studying calculus, then you’re probably familiar with the concepts of increasing and decreasing functions. These terms refer to the behavior of a function as its input values change. Specifically, an increasing function is one that becomes larger as its input values increase, while a decreasing function is one that becomes smaller as its input values increase. Understanding these concepts is crucial for solving a variety of calculus problems, from finding maximum and minimum values to understanding the behavior of graphs.
In this article, we’ll delve deeper into increasing and decreasing functions, exploring how to identify them, and how to use them to solve problems in calculus.
Increasing Function Definition
In simple words, an increasing function is a type of function where with increasing input (or the independent variable), output also increases (or the value of the function). Now, let’s define increasing function formally.
Now, let us consider I to be an interval that presents in the domain of a real-valued function f, then the function f is increasing on I,
if x1 < x2 ⇒ f(x1) ≤ f(x2) ∀ x1 and x2 ∈ I
Some common examples of increasing functions include linear functions with positive slope (such as y = mx + b), exponential functions (such as y = ax, where a is a positive constant), and power functions (such as y = xn, where n is a positive integer).
Strictly Increasing Function
For a function to be strictly increasing, the function should be increasing but it can’t be equal for any two unequal values i.e.,
if x1 < x2 ⇒ f(x1) < f(x2) ∀ x1 and x2 ∈ I
Decreasing Function Definition
In simple words, a decreasing function is a type of function where with increasing input (or the independent variable), the output value decreases (or the value of the function). To define decreasing function formally let us consider I to be an interval that presents in the domain of a real-valued function f, then the function f is increasing on I,
if x1 < x2 ⇒ f(x1) ≥ f(x2) ∀ x1 and x2 ∈ I
Some common examples of decreasing functions include exponential decay functions (such as y = a^(-x), where a is a positive constant), and negative power functions (such as y = x^(-n), where n is a positive integer).
Strictly Decreasing Function
For a function to be strictly decreasing, the function should be decreasing but it can’t be equal for any two unequal values i.e.,
if x1 < x2 ⇒ f(x1) > f(x2) ∀ x1 and x2 ∈ I
Constant Function Definition
In simple words, a constant function is a type of function where regardless of the input or independent variable the output always remains the same i.e., for all the inputs output remains constant. To define a constant function more formally, a function f is said to be a constant function if and only if
f(x) = k
Where k is the real number.
Rules to Check Increasing and Decreasing Functions
In calculus, the increasing function can be defined in terms of the slope of any curve as an increasing function always has a positive slope i.e., dy/dx > 0. To define increasing function more formally, let us consider f to be a function that is continuous on the interval [p, q] and differentiable on the open interval (p, q), then
Function f is increasing in [p, q] if f′(x) > 0 for each x ∈ (p, q).
As decreasing function always has a negative slope, thus a decreasing function can be defined in terms of the slope of any curve i.e., dy/dx < 0. For a more formal definition of the decreasing function, let us consider f to be a function that is continuous on the interval [p, q] and differentiable on the open interval (p, q), then
Function f is decreasing in [p, q] if f′(x) < 0 for each x ∈ (p, q).
Graph of Increasing, Decreasing, and Constant Function
The graphical representation of an increasing function, decreasing function, and constant function is,
Example: In this example, we will investigate the graph of f(x) = x2.
Solution:
| x | f(x) |
|---|
| -4 | 16 |
| -3 | 9 |
| -2 | 4 |
| -1 | 1 |
| 0 | 0 |
| 1 | 1 |
| 2 | 4 |
| 3 | 9 |
| 4 | 16 |
As we can see that when x < 0, the value of f(x) is decreasing as the graph moves to the right. In other words, the “height” of the graph is getting smaller. This is also confirmed by looking at the table of values. When x < 0, as x increases, f(x) decreases. Therefore, f(x) is decreasing on the interval from negative infinity to 0.
When x > 0, the opposite is happening. When x > 0, the value of f(x) is increasing as the graph moves to the right. In other words, the “height” of the graph is getting bigger. This is also confirmed by looking at the table of values. When x > 0, as x increases, f(x) increases. Therefore, f(x) is increasing on the interval from 0 to infinity.
Properties of Increasing & Decreasing Functions
Some helpful algebraic properties of Increasing & Decreasing Functions are as follows:
- Additive property. If the functions f and g are increasing/decreasing on the interval (a, b), then the sum of the functions f + g is also increasing/decreasing on this interval.
- Opposite property. If the function f is increasing/decreasing on the interval (a, b), then the opposite function, -f, is decreasing/increasing.
- Inverse property. If the function f is increasing/decreasing on the interval (a, b), then the inverse function, 1/f, is decreasing/increasing on this interval.
- Multiplicative property. If the functions f and g are increasing/decreasing and not negative on the interval (a, b), then the product of the functions is also increasing/decreasing.
How to Find Increasing and Decreasing Intervals
Given a function, f(x), we can determine the intervals where it is increasing and decreasing by using differentiation and algebra.
Step 1: Find the derivative, f'(x), of the function.
Step 2: Find the zeros of f'(x). Remember, zeros are the values of x for which f'(x) = 0. Set f'(x) = 0 and solve for x.
Step 3: Determine the intervals. The intervals are between the endpoints of the interval of f(x) and the zeros of f'(x). If the interval of f(x) is not given, assume f(x) is on the interval (-∞, ∞).
Step 4: Determine whether the function is increasing or decreasing on each interval. Given the interval (a, c), choose a value b, a < b < c. Solve for f'(b). If f'(b) is positive, f(x) is increasing on (a, c). If f'(b) is negative, f(x) is decreasing on (a, c).
Example: If g(x) = (x – 5)2, find the intervals where g(x) is increasing and decreasing.
Solution:
Step 1: Find the derivative of the function.
Using the chain rule,
g'(x) = 2(5 – x)
Step 2: Find the zeros of the derivative function.
In other words, find the values of for which g(x) equals zero. You can do this by setting g(x) = 0 and using algebra to solve for x. From the definitions above, we know the function is constant at points where the derivative is zero.
g'(x) = 0 = 2(5 – x)
0 = 5 – x
x = 5
Step 3: Use the zeros to determine intervals.
Since x = 5 is the only zero for g'(x), there are just 2 intervals: from negative infinity to 5, and from 5 to negative infinity.
These can be denoted in inequality notation:
-∞ < x < 5
5 < x < ∞
Or in interval notation:
(-∞, 5), (5, ∞)
Remember, the endpoints are NOT inclusive because g(x) is neither increasing nor decreasing at the endpoints.
Step 4: Determine if the function is increasing or decreasing in each interval.
For the first interval, ((-∞, 5), we’ll choose b = 0. -∞ < x < 5
g'(b) = g'(0) = 2(5-0) = 10
10 > 0 POSITIVE
For the second interval, (5, ∞), we’ll choose b = 6. 5 < 6 < ∞
g'(b) = g'(6) = 2(5-6) = -2
-2 < 0 NEGATIVE
Therefore, g(x) is increasing on (-∞, 5) and decreasing on (5, ∞). We can verify our results visually. In the graph below, you can clearly see that f(x) = (x – 5)2 is increasing on the interval (5, ∞) and decreasing on the interval (-∞, 5).
We can visually verify our result by investigating the graph of g(x).
Looking at the graph, g(x) is indeed increasing in the interval from negative infinity to 5 and decreasing in the interval from 5 to infinity.
Example: Find the intervals in -20 < x < 20 where g(x) is increasing and decreasing given g'(x) = x2 – 100.
Solution:
If the derivative is given, we can skip the first step and go straight to finding the zeroes.
g'(x)= 0 = x2 – 100
x2 = 100
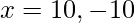
Intervals: (-20, -10), (-10, 10), (10, 20)
For (-20, -10), we’ll choose b = -12. -20 < -12 < -10
g'(-12) = 44 > 0
For (-10, 10), we’ll choose b = 0. -10 < 0 < 10
g(0) = -100 < 0
For (10, 20), we’ll choose b = 12. 10 < 12 < 20
g(12) = 44 > 0
Hence, for -20 < x < 20, g(x) is increasing on (-20, -10) and (10, 20) and decreasing on (-10, 10).
Read More,
Sample Problems on Increasing and Decreasing Functions
Problem 1: Given the function g(x) = 3x2 – 12, find the intervals on -3 < x < 3 where g(x) is increasing and decreasing.
Solution:
Given function: g(x) = 3x2 – 12
Differentiate w.r.t. x, we get
g'(x) = 6x
For increasing and decreasing
Put g'(x) = 0
g'(x) = 6x = 0
So, x = 0
Intervals: (-3, 0), (0, 3)
At x = -2, g'(-2) = -12 < 0
At x = 2, g'(2) = 12 > 0
So, for -3 < x < 3, g(x) is decreasing on (-3, 0) and increasing on (0, 3).
Problem 2: Given the derivative of f(x), f'(x) = -10x2 + 40x, find the intervals where f(x) is increasing and decreasing.
Solution:
Given: f'(x) = -10x2 + 40x
For increasing and decreasing
Put f'(x) = 0
f'(x) = -10x2 + 40x = 0
So, x = 4, 0
Intervals: (−∞, 0), (0, 4), (4, ∞)
So, at x = -1, f'(-1) = -50 < 0
at x = 1, f'(1) = 30 > 0
at x = 5, f'(5) = -50 < 0
So, f(x) is increasing on (0, 4) and decreasing on (−∞, 0), (4, ∞)
Problem 3: Given the function g(x) = 5x2 – 20x + 100, find the intervals where g(x) is increasing and decreasing.
Solution:
Given: g(x) = 5x2 – 20x + 100
Differentiate w.r.t. x, we get
g'(x) = 10x – 20
For increasing and decreasing
Put g'(x) = 0
g'(x) = 10x – 20 = 0
x = 2
Intervals: (−∞, 2), (2, ∞)
At, x = 1, g'(1) = -10 < 0
At x = 3, g'(3) = 10 > 0
So, g(x) is decreasing on (-∞, 2) and increasing on (2, ∞)
Problem 4: Given the function s(x) = 6x3 – x2, find the intervals on 0 < x < 10 where s(x) is increasing and decreasing.
Solution:
Given: s(x) = 6x3 – x2
Differentiate w.r.t. x, we get
s'(x) = 18x2 – 2x
For increasing and decreasing
Put s'(x) = 0
s'(x) = 18x2 – 2x = 0
x = 1/9, -1/9
Intervals: (0, 1/9)
Here, -1/9 is not in the given interval, 0 < x < 10
So, g'(1/10) = -0.02 < 0
Hence, for 0 < x < 10, g(x) is decreasing on (0, 1/9)
Problem 5: Given g'(x) = 7x2 – 8, find the intervals where g(x) is increasing and decreasing.
Solution:
Given: g'(x) = 7x2 – 8
For increasing and decreasing
Put g'(x) = 0
g'(x) = 7x2 – 8 = 0
x = {√(8/7), -√(8/7)}
Intervals: (-∞,√(8/7)), (-√(8/7), √(8/7)), (√(8/7), ∞)
So, At x = -10, g'(-10) = 692 > 0
At x = 0, g'(0) = -8 < 0
At x = 10, g'(10) = 692 < 0
Hence, g(x) is increasing on (-∞,√(8/7))and (√(8/7), ∞), and decreasing on (-√(8/7), √(8/7))
FAQs on Increasing and Decreasing Functions
Q1: Define Increasing Function.
Answer:
An increasing function is a function where if you take two input values, the function value at the higher input value will be greater than or equal to the function value at the lower input value.
Q2: Define Decreasing Function.
Answer:
A decreasing function is a function where if you take two input values, the function value at the higher input value will be less than or equal to the function value at the lower input value.
Q3: How to tell if Any Given Function is Increasing or Decreasing?
Answer:
To determine if a function is increasing or decreasing, you can look at the sign of the first derivative. If the first derivative is positive, then the function is increasing. If the first derivative is negative, then the function is decreasing.a
Q4: Can a Function be both Increasing and Decreasing?
Answer:
No, a function cannot be both increasing and decreasing. If a function is increasing on an interval, it cannot be decreasing on the same interval, and vice versa. However, a function can have different intervals of increasing and decreasing behavior.
Q5: What is a Strictly Increasing Function?
Answer:
A strictly increasing function is a function where the value of the function strictly increases as the input value increases. In other words, if you take two input values, the function value at the higher input value will always be greater than the function value at the lower input value.
Q6: What is a Strictly Decreasing Function?
Answer:
A strictly decreasing function is a function where the value of the function strictly decreases as the input value increases. In other words, if you take two input values, the function value at the higher input value will always be less than the function value at the lower input value.
Q7: What is a Monotonic Function?
Answer:
A monotonic function is a function that is either strictly increasing or strictly decreasing.
Share your thoughts in the comments
Please Login to comment...