Halting Problem in Theory of Computation
Last Updated :
20 Nov, 2019
To understand better the halting problem, we must know Decidability, Undecidability and Turing machine, decision problems and also a theory named as Computability theory and Computational complexity theory.
Some important terms:
- Computability theory –
The branch of theory of computation that studies which problems are computationally solvable using different model. In computer science, the computational complexity, or simply complexity of an algorithm is the amount of resources required for running it.
- Decision problems –
A decision problem has only two possible outputs (yes or no) on any input. In computability theory and computational complexity theory, a decision problem is a problem that can be posed as a yes-no question of the input values. Like is there any solution to a particular problem? The answer would be either a yes or no. A decision problem is any arbitrary yes/no question on an infinite set of inputs.
- Turing machine –
A Turing machine is a mathematical model of computation. A Turing machine is a general example of a CPU that controls all data manipulation done by a computer. Turing machine can be halting as well as non halting and it depends on algorithm and input associated with the algorithm.
Now, lets discuss Halting problem:
The Halting problem – Given a program/algorithm will ever halt or not?
Halting means that the program on certain input will accept it and halt or reject it and halt and it would never go into an infinite loop. Basically halting means terminating. So can we have an algorithm that will tell that the given program will halt or not. In terms of Turing machine, will it terminate when run on some machine with some particular given input string.
The answer is no we cannot design a generalized algorithm which can appropriately say that given a program will ever halt or not?
The only way is to run the program and check whether it halts or not.
We can refrain the halting problem question in such a way also: Given a program written in some programming language(c/c++/java) will it ever get into an infinite loop(loop never stops) or will it always terminate(halt)?
This is an undecidable problem because we cannot have an algorithm which will tell us whether a given program will halt or not in a generalized way i.e by having specific program/algorithm.In general we can’t always know that’s why we can’t have a general algorithm.The best possible way is to run the program and see whether it halts or not.In this way for many programs we can see that it will sometimes loop and always halt.
Proof by Contradiction –
Problem statement: Can we design a machine which if given a program can find out if that program will always halt or not halt on a particular input?
Solution: Let us assume that we can design that kind of machine called as HM(P, I) where HM is the machine/program, P is the program and I is the input. On taking input the both arguments the machine HM will tell that the program P either halts or not.
If we can design such a program this allows us to write another program we call this program CM(X) where X is any program(taken as argument) and according to the definition of the program CM(X) shown in the figure.

In the program CM(X) we call the function HM(X), which we have already defined and to HM() we pass the arguments (X, X), according to the definition of HM() it can take two arguments i.e one is program and another is the input.Now in the second program we pass X as a program and X as input to the function HM().We know that the program HM() gives two output either “Halt” or “Not Halt”.But in case second program, when HM(X, X) will halt loop body tells to go in loop and when it doesn’t halt that means loop, it is asked to return.
Now we take one more situation where the program CM is passed to CM() function as an argument. Then there would be some impossibility, i.e., a condition arises which is not possible.
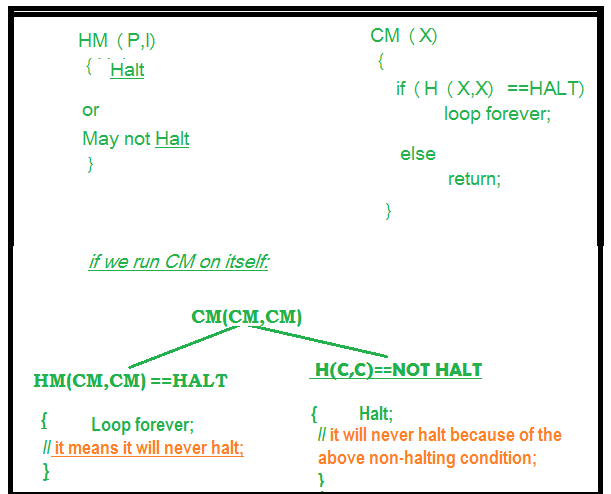
It is impossible for outer function to halt if its code (inner body) is in loop and also it is impossible for outer non halting function to halt even after its inner code is halting. So the both condition is non halting for CM machine/program even we had assumed in the beginning that it would halt.So this is the contradiction and we can say that our assumption was wrong and this problem, i.e., halting problem is undecidable.
This is how we proved that halting problem is undecidable.
Share your thoughts in the comments
Please Login to comment...