Dinic’s algorithm for Maximum Flow
Last Updated :
13 Mar, 2023
Problem Statement :
Given a graph that represents a flow network where every edge has a capacity. Also given two vertices source ‘s’ and sink ‘t’ in the graph, find the maximum possible flow from s to t with the following constraints :
- Flow on an edge doesn’t exceed the given capacity of the edge.
- An incoming flow is equal to an outgoing flow for every vertex except s and t.
For example:
In the following input graph,
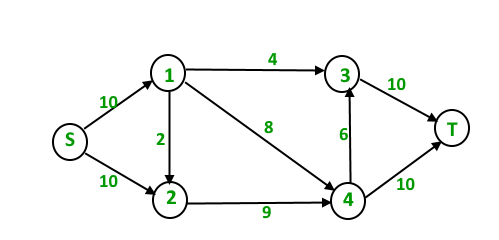
the maximum s-t flow is 19 which is shown below.
Background :
- Max Flow Problem Introduction: We introduced the Maximum Flow problem, discussed Greedy Algorithm, and introduced the residual graph.
- Ford-Fulkerson Algorithm and Edmond Karp Implementation: We discussed the Ford-Fulkerson algorithm and its implementation. We also discussed the residual graph in detail.
The time complexity of Edmond Karp Implementation is O(VE2). In this post, a new Dinic’s algorithm is discussed which is a faster algorithm and takes O(EV2).
Like Edmond Karp’s algorithm, Dinic’s algorithm uses following concepts :
- A flow is maximum if there is no s to t path in residual graph.
- BFS is used in a loop. There is a difference though in the way we use BFS in both algorithms.
In Edmond’s Karp algorithm, we use BFS to find an augmenting path and send flow across this path. In Dinic’s algorithm, we use BFS to check if more flow is possible and to construct level graph. In level graph, we assign levels to all nodes, level of a node is shortest distance (in terms of number of edges) of the node from source. Once level graph is constructed, we send multiple flows using this level graph. This is the reason it works better than Edmond Karp. In Edmond Karp, we send only flow that is send across the path found by BFS.
Outline of Dinic’s algorithm :
- Initialize residual graph G as given graph.
- Do BFS of G to construct a level graph (or assign levels to vertices) and also check if more flow is possible.
- If more flow is not possible, then return
- Send multiple flows in G using level graph until blocking flow is reached.
Here using level graph means, in every flow, levels of path nodes should be 0, 1, 2…(in order) from s to t.
A flow is Blocking Flow if no more flow can be sent using level graph, i.e., no more s-t path exists such that path vertices have current levels 0, 1, 2… in order. Blocking Flow can be seen same as maximum flow path in Greedy algorithm discussed here.
Illustration :
Initial Residual Graph (Same as given Graph)

Total Flow = 0
First Iteration : We assign levels to all nodes using BFS. We also check if more flow is possible (or there is a s-t path in residual graph).

Now we find blocking flow using levels (means every flow path should have levels as 0, 1, 2, 3). We send three flows together. This is where it is optimized compared to Edmond Karp where we send one flow at a time.
4 units of flow on path s – 1 – 3 – t.
6 units of flow on path s – 1 – 4 – t.
4 units of flow on path s – 2 – 4 – t.
Total flow = Total flow + 4 + 6 + 4 = 14
After one iteration, residual graph changes to following.

Second Iteration : We assign new levels to all nodes using BFS of above modified residual graph. We also check if more flow is possible (or there is a s-t path in residual graph).

Now we find blocking flow using levels (means every flow path should have levels as 0, 1, 2, 3, 4). We can send only one flow this time.
5 units of flow on path s – 2 – 4 – 3 – t
Total flow = Total flow + 5 = 19
The new residual graph is

Third Iteration : We run BFS and create a level graph. We also check if more flow is possible and proceed only if possible. This time there is no s-t path in residual graph, so we terminate the algorithm.
Implementation :
Below is c++ implementation of Dinic’s algorithm:
CPP
#include <bits/stdc++.h>
using namespace std;
struct Edge {
int v;
int flow;
int C;
int rev;
};
class Graph {
int V;
int* level;
vector<Edge>* adj;
public:
Graph(int V)
{
adj = new vector<Edge>[V];
this->V = V;
level = new int[V];
}
void addEdge(int u, int v, int C)
{
Edge a{ v, 0, C, (int)adj[v].size() };
Edge b{ u, 0, 0, (int)adj[u].size() };
adj[u].push_back(a);
adj[v].push_back(b);
}
bool BFS(int s, int t);
int sendFlow(int s, int flow, int t, int ptr[]);
int DinicMaxflow(int s, int t);
};
bool Graph::BFS(int s, int t)
{
for (int i = 0; i < V; i++)
level[i] = -1;
level[s] = 0;
list<int> q;
q.push_back(s);
vector<Edge>::iterator i;
while (!q.empty()) {
int u = q.front();
q.pop_front();
for (i = adj[u].begin(); i != adj[u].end(); i++) {
Edge& e = *i;
if (level[e.v] < 0 && e.flow < e.C) {
level[e.v] = level[u] + 1;
q.push_back(e.v);
}
}
}
return level[t] < 0 ? false : true;
}
int Graph::sendFlow(int u, int flow, int t, int start[])
{
if (u == t)
return flow;
for (; start[u] < adj[u].size(); start[u]++) {
Edge& e = adj[u][start[u]];
if (level[e.v] == level[u] + 1 && e.flow < e.C) {
int curr_flow = min(flow, e.C - e.flow);
int temp_flow
= sendFlow(e.v, curr_flow, t, start);
if (temp_flow > 0) {
e.flow += temp_flow;
adj[e.v][e.rev].flow -= temp_flow;
return temp_flow;
}
}
}
return 0;
}
int Graph::DinicMaxflow(int s, int t)
{
if (s == t)
return -1;
int total = 0;
while (BFS(s, t) == true) {
int* start = new int[V + 1]{ 0 };
while (int flow = sendFlow(s, INT_MAX, t, start)) {
total += flow;
}
delete[] start;
}
return total;
}
int main()
{
Graph g(6);
g.addEdge(0, 1, 16);
g.addEdge(0, 2, 13);
g.addEdge(1, 2, 10);
g.addEdge(1, 3, 12);
g.addEdge(2, 1, 4);
g.addEdge(2, 4, 14);
g.addEdge(3, 2, 9);
g.addEdge(3, 5, 20);
g.addEdge(4, 3, 7);
g.addEdge(4, 5, 4);
cout << "Maximum flow " << g.DinicMaxflow(0, 5);
return 0;
}
|
Java
import java.util.*;
class Edge {
public int v;
public int flow;
public int C;
public int rev;
public Edge(int v, int flow, int C, int rev) {
this.v = v;
this.flow = flow;
this.C = C;
this.rev = rev;
}
}
class Graph {
private int V;
private int[] level;
private List<Edge>[] adj;
public Graph(int V) {
adj = new ArrayList[V];
for (int i = 0; i < V; i++) {
adj[i] = new ArrayList<Edge>();
}
this.V = V;
level = new int[V];
}
public void addEdge(int u, int v, int C) {
Edge a = new Edge(v, 0, C, adj[v].size());
Edge b = new Edge(u, 0, 0, adj[u].size());
adj[u].add(a);
adj[v].add(b);
}
public boolean BFS(int s, int t) {
for (int i = 0; i < V; i++) {
level[i] = -1;
}
level[s] = 0;
LinkedList<Integer> q = new LinkedList<Integer>();
q.add(s);
ListIterator<Edge> i;
while (q.size() != 0) {
int u = q.poll();
for (i = adj[u].listIterator(); i.hasNext();) {
Edge e = i.next();
if (level[e.v] < 0 && e.flow < e.C) {
level[e.v] = level[u] + 1;
q.add(e.v);
}
}
}
return level[t] < 0 ? false : true;
}
public int sendFlow(int u, int flow, int t, int start[]) {
if (u == t) {
return flow;
}
for (; start[u] < adj[u].size(); start[u]++) {
Edge e = adj[u].get(start[u]);
if (level[e.v] == level[u] + 1 && e.flow < e.C) {
int curr_flow = Math.min(flow, e.C - e.flow);
int temp_flow = sendFlow(e.v, curr_flow, t, start);
if (temp_flow > 0) {
e.flow += temp_flow;
adj[e.v].get(e.rev).flow -= temp_flow;
return temp_flow;
}
}
}
return 0;
}
public int DinicMaxflow(int s, int t) {
if (s == t) {
return -1;
}
int total = 0;
while (BFS(s, t) == true) {
int[] start = new int[V + 1];
while (true) {
int flow = sendFlow(s, Integer.MAX_VALUE, t, start);
if (flow == 0) {
break;
}
total += flow;
}
}
return total;
}
}
public class Main {
public static void main(String args[]) {
Graph g = new Graph(6);
g.addEdge(0, 1, 16);
g.addEdge(0, 2, 13);
g.addEdge(1, 2, 10);
g.addEdge(1, 3, 12);
g.addEdge(2, 1, 4);
g.addEdge(2, 4, 14);
g.addEdge(3, 2, 9);
g.addEdge(3, 5, 20);
g.addEdge(4, 3, 7);
g.addEdge(4, 5, 4);
System.out.println("Maximum flow " + g.DinicMaxflow(0, 5));
}
}
|
Python3
class Edge:
def __init__(self, v, flow, C, rev):
self.v = v
self.flow = flow
self.C = C
self.rev = rev
class Graph:
def __init__(self, V):
self.adj = [[] for i in range(V)]
self.V = V
self.level = [0 for i in range(V)]
def addEdge(self, u, v, C):
a = Edge(v, 0, C, len(self.adj[v]))
b = Edge(u, 0, 0, len(self.adj[u]))
self.adj[u].append(a)
self.adj[v].append(b)
def BFS(self, s, t):
for i in range(self.V):
self.level[i] = -1
self.level[s] = 0
q = []
q.append(s)
while q:
u = q.pop(0)
for i in range(len(self.adj[u])):
e = self.adj[u][i]
if self.level[e.v] < 0 and e.flow < e.C:
self.level[e.v] = self.level[u]+1
q.append(e.v)
return False if self.level[t] < 0 else True
def sendFlow(self, u, flow, t, start):
if u == t:
return flow
while start[u] < len(self.adj[u]):
e = self.adj[u][start[u]]
if self.level[e.v] == self.level[u]+1 and e.flow < e.C:
curr_flow = min(flow, e.C-e.flow)
temp_flow = self.sendFlow(e.v, curr_flow, t, start)
if temp_flow and temp_flow > 0:
e.flow += temp_flow
self.adj[e.v][e.rev].flow -= temp_flow
return temp_flow
start[u] += 1
def DinicMaxflow(self, s, t):
if s == t:
return -1
total = 0
while self.BFS(s, t) == True:
start = [0 for i in range(self.V+1)]
while True:
flow = self.sendFlow(s, float('inf'), t, start)
if not flow:
break
total += flow
return total
g = Graph(6)
g.addEdge(0, 1, 16)
g.addEdge(0, 2, 13)
g.addEdge(1, 2, 10)
g.addEdge(1, 3, 12)
g.addEdge(2, 1, 4)
g.addEdge(2, 4, 14)
g.addEdge(3, 2, 9)
g.addEdge(3, 5, 20)
g.addEdge(4, 3, 7)
g.addEdge(4, 5, 4)
print("Maximum flow", g.DinicMaxflow(0, 5))
|
C#
using System;
using System.Collections.Generic;
class Edge {
public int v;
public int flow;
public int C;
public int rev;
public Edge(int v, int flow, int C, int rev) {
this.v = v;
this.flow = flow;
this.C = C;
this.rev = rev;
}
}
class Graph {
private int V;
private int[] level;
private List<Edge>[] adj;
public Graph(int V) {
adj = new List<Edge>[V];
for (int i = 0; i < V; i++) {
adj[i] = new List<Edge>();
}
this.V = V;
level = new int[V];
}
public void addEdge(int u, int v, int C) {
Edge a = new Edge(v, 0, C, adj[v].Count);
Edge b = new Edge(u, 0, 0, adj[u].Count);
adj[u].Add(a);
adj[v].Add(b);
}
public bool BFS(int s, int t) {
for (int j = 0; j < V; j++) {
level[j] = -1;
}
level[s] = 0;
Queue<int> q = new Queue<int>();
q.Enqueue(s);
List<Edge>.Enumerator i;
while (q.Count != 0) {
int u = q.Dequeue();
for (i = adj[u].GetEnumerator(); i.MoveNext();) {
Edge e = i.Current;
if (level[e.v] < 0 && e.flow < e.C) {
level[e.v] = level[u] + 1;
q.Enqueue(e.v);
}
}
}
return level[t] < 0 ? false : true;
}
public int sendFlow(int u, int flow, int t, int[] start) {
if (u == t) {
return flow;
}
for (; start[u] < adj[u].Count; start[u]++) {
Edge e = adj[u][start[u]];
if (level[e.v] == level[u] + 1 && e.flow < e.C) {
int curr_flow = Math.Min(flow, e.C - e.flow);
int temp_flow = sendFlow(e.v, curr_flow, t, start);
if (temp_flow > 0) {
e.flow += temp_flow;
adj[e.v][e.rev].flow -= temp_flow;
return temp_flow;
}
}
}
return 0;
}
public int DinicMaxflow(int s, int t) {
if (s == t) {
return -1;
}
int total = 0;
while (BFS(s, t) == true) {
int[] start = new int[V + 1];
while (true) {
int flow = sendFlow(s, int.MaxValue, t, start);
if (flow == 0) {
break;
}
total += flow;
}
}
return total;
}
}
public class Gfg {
public static void Main() {
Graph g = new Graph(6);
g.addEdge(0, 1, 16);
g.addEdge(0, 2, 13);
g.addEdge(1, 2, 10);
g.addEdge(1, 3, 12);
g.addEdge(2, 1, 4);
g.addEdge(2, 4, 14);
g.addEdge(3, 2, 9);
g.addEdge(3, 5, 20);
g.addEdge(4, 3, 7);
g.addEdge(4, 5, 4);
Console.Write("Maximum flow " + g.DinicMaxflow(0, 5));
}
}
|
Javascript
class Edge {
constructor(v, flow, C, rev) {
this.v = v;
this.flow = flow;
this.C = C;
this.rev = rev;
}
}
class Graph {
constructor(V) {
this.V = V;
this.adj = Array.from(Array(V), () => new Array());
this.level = new Array(V);
}
addEdge(u, v, C) {
let a = new Edge(v, 0, C, this.adj[v].length);
let b = new Edge(u, 0, 0, this.adj[u].length);
this.adj[u].push(a);
this.adj[v].push(b);
}
BFS(s, t) {
for (let i = 0; i < this.V; i++) this.level[i] = -1;
this.level[s] = 0;
let q = new Array();
q.push(s);
while (q.length != 0) {
let u = q[0];
q.shift();
for (let j in this.adj[u]) {
let e = this.adj[u][j];
if (this.level[e.v] < 0 && e.flow < e.C) {
this.level[e.v] = this.level[u] + 1;
q.push(e.v);
}
}
}
return this.level[t] < 0 ? false : true;
}
sendFlow(u, flow, t, start) {
if (u == t) return flow;
while (start[u] < this.adj[u].length) {
let e = this.adj[u][start[u]];
if (this.level[e.v] == this.level[u] + 1 && e.flow < e.C) {
let curr_flow = Math.min(flow, e.C - e.flow);
let temp_flow = this.sendFlow(e.v, curr_flow, t, start);
if (temp_flow > 0) {
e.flow += temp_flow;
this.adj[e.v][e.rev].flow -= temp_flow;
return temp_flow;
}
}
start[u] = start[u] + 1;
}
return 0;
}
DinicMaxflow(s, t) {
if (s == t) return -1;
let total = 0;
while (this.BFS(s, t) == true) {
let start = new Array(this.V + 1);
start.fill(0);
while (true) {
let flow = this.sendFlow(s, Number.MAX_VALUE, t, start);
if (!flow) {
break;
}
total += flow;
}
}
return total;
}
}
let g = new Graph(6);
g.addEdge(0, 1, 16);
g.addEdge(0, 2, 13);
g.addEdge(1, 2, 10);
g.addEdge(1, 3, 12);
g.addEdge(2, 1, 4);
g.addEdge(2, 4, 14);
g.addEdge(3, 2, 9);
g.addEdge(3, 5, 20);
g.addEdge(4, 3, 7);
g.addEdge(4, 5, 4);
console.log("Maximum flow " + g.DinicMaxflow(0, 5));
|
Time Complexity : O(EV2).
- Doing a BFS to construct level graph takes O(E) time.
- Sending multiple more flows until a blocking flow is reached takes O(VE) time.
- The outer loop runs at-most O(V) time.
- In each iteration, we construct new level graph and find blocking flow. It can be proved that the number of levels increase at least by one in every iteration (Refer the below reference video for the proof). So the outer loop runs at most O(V) times.
- Therefore overall time complexity is O(EV2).
Space complexity:
The space complexity of Dinic’s algorithm is O(V+E), since it requires O(V) to store the level array and O(E) to store the graph’s adjacency list.
Share your thoughts in the comments
Please Login to comment...