Things are often referred similar when the physical structure or patterns they show are having similar properties, Sometimes two objects may vary in size but because of their physical similarities, they are called similar objects. For example, a bigger Square will always be similar to a smaller square. In Triangles, if the sizes vary but the shape they have are alike, then the Triangles can be called Similar Triangles. When two triangles are declared Similar, their corresponding angles are always congruent (Identical in form), and their sides are Proportional. Let’s learn more about the similarities of triangles.
Similar Triangles
Two or more than two triangles are similar when their corresponding angles are congruent and their sides are proportional to each other(the ratio of their sides are equal). Noticing things from our daily life or a good look in our textbooks tell us that there are so many objects similar to each other we have never noticed, For Instance, a baby bear looks alike its mother even though the mother is relatively bigger, the same concept is applied here in triangles.

ΔABC and ΔPQR are Similar Triangles
Difference between Similar Triangles and Congruent Triangles
- In Similar Triangles, Shape is always same, but Size may vary.
- In Congruent Triangles, Both shape and size are equal.

ΔABC and ΔPQR are congruent Triangles
Thales Theorem or Basic Proportionality Theorem
A Famous Greek Mathematics “Thales” gave a universal Theorem for Triangles, “In two Triangles that are Equiangular(Corresponding angles of both triangles are equal), the Ratio of their corresponding sides are always equal.”

Two Triangles ΔABC and ΔADE shown in one
As we can notice, the above given Two triangles are equiangular.
∠A = ∠A [Common Angle]
∠B = ∠D [Corresponding Angles]
∠C = ∠E [Corresponding Angles]
Therefore, it is concluded “If a line is drawn parallel to one side of the triangle to intersect on remaining two sides, it will divide the remaining two sides in the same ratio”
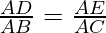 , DF//BC
, DF//BC
Proof of Thales Theorem
If a line is drawn parallel to one side of a triangle, intersecting other sides at distinct points, then the division of the other two sides is in the same ratio
To Prove:
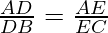
Given:
In ΔABC, DE is parallel to BC
Construction:
Join BE and CD and draw perpendicular to AC and AB from D and E.
Proof:

In ΔADE, Area of triangle = 1/2 × DE × EN ⇢ 1
Also, 1/2 × DE× DM ⇢ 2
In ΔBDE, Area of Triangle =1/2 × BD × EN ⇢ 3
In ΔDEC, Area of Triangle= 1/2 × EC × DM ⇢ 4
Dividing equation 1 and 3
 ⇢ 5
⇢ 5
Dividing equation 2 and 4
\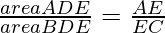 ⇢ 6
⇢ 6
We know, area of ΔBDE and ΔDEC are equal, since BD is parallel to DE and they both have the same base DE
Now, from equation 5 and 6
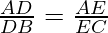
Converse of Thales Theorem
If a line divides any two sides of the triangle in the same ratio, then the line is parallel to the third side of the triangle
Proof:

Given:
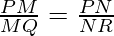
Construction:
Lets assume that line MN is not parallel to QR, Draw another line MK such that MK is parallel to QR
Now, in ΔPQR,
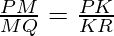 ⇢ 1
⇢ 1
but, this is also provided that,
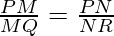 ⇢ 2
⇢ 2
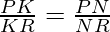
But, K and N lie on the same line PR, Therefore, they coincide each other and are just the same point.
Therefore, MN and MK are the same line and MN is parallel to QR.
Criteria for Similarity of Triangles
Two triangles are called similar when their angles are equal and their corresponding sides are always in the same ratio, this is what we have learned so far, however one does not need to prove all the things mentioned above to show similarity of two triangles. There are 3 easier ways to find out if the two triangles are similar.
Theorem 1: SSS Similarity Criterion
It states if in a triangle, all the sides are proportional to the sides of other triangles, then the corresponding angles will always be equal and hence, both triangles are Similar.
Proof:

To Prove: 
Given: ∠A=∠D, ∠B=∠E, ∠C=∠F
Construction: Draw a line PQ in ΔDEF such that AB = DP, AC = DQ, BC = PQ

Proof: 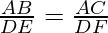
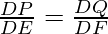
Reciprocal the fraction, 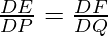
Subtract equation by 1 on both sides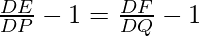
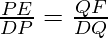
By the converse of BPT, PQ is parallel to EF
Therefore, ∠P = ∠E, ∠Q = ∠F (by corresponding angles)
Therefore, ΔDEF∼ ΔDPQ

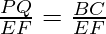
BC=PQ, AB=DP, AC=DQ
ΔABC≅ ΔDPQ
∠A= ∠D, ∠B= ∠P, ∠C= ∠Q, ∠B= ∠E, ∠C= ∠F,
Hence, ΔABC ∼ ΔDEF
Theorem 2: AAA OR AA Similarity Criterion
AAA referring to angles (all three) of the triangles. It states “If the two corresponding angles both the triangles are equal, then their respective sides will always have same ratio and the triangles are similar triangles”
AA is another name for the theorem since having two angles equal will automatically make the third angle of the triangles equal as the sum is always 180°.
Proof:

Given: ∠A = ∠D, ∠B = ∠E, ∠C = ∠F
To Prove: 
Construction: Make a line PQ in ΔDEF such that AB=DP, AC=DQ, BC=PQ

Proof: In ΔABC and ΔDPQ
AB=DP, AC=DQ, ∠A=∠D
By S.A.S Property of triangles, both the triangles are congruent to each other.
ΔABC≅ ΔDPQ
We can say, ∠B= ∠DPQ (By CPCT)
∠B= ∠E, Therefore ∠E = ∠DPQ
By corresponding angles, it can be concluded that PQ is parallel to EF
With the help of Converse of Thales theorem,
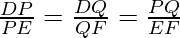
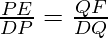
Adding 1 to both LHS and RHS
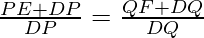
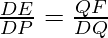
Replace DP with AB and DQ with AC
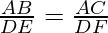
Therefore, the ratio of corresponding sides is coming out to be equal as well.
Hence, ΔABC= ΔDEF
Theorem 3: SAS Similarity Criterion
If the two angles of both the triangles along with both the sides connected to them are equal, then the triangles are called Similar Triangles.
Proof

To Prove: ΔABC∼ ΔDEF
Given: ∠A= ∠D, 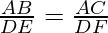
Construction: Draw a line PQ in triangle ΔDEF Such that AB= DP, AC=DQ

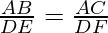
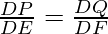
Reciprocate the fraction, 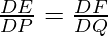
Subtracting both sides by 1, 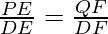
So, PQ is parallel to EF (by converse of BPT)
∠P= ∠E, ∠Q= ∠F (by corresponding angles)
ΔABC= ΔDPQ
∠A= ∠D, ∠B=∠P, ∠C=∠Q
Since ∠P=∠E, ∠Q= ∠F
Therefore, ∠A=∠D, ∠B= ∠E, ∠C= ∠F
ΔABC∼ ΔDEF
Pythagoras Theorem
In a right-angled Triangle, the square of the hypotenuse is equal to the sum of squares of other two sides
Proof:
Given: ΔPQR is a right angled Triangle and QS is perpendicular to PR
Proof:

We know that, ∠PQR= ∠QSR
∠P= ∠P
Therefore, Δ PQR∼ ΔQSR
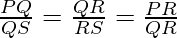
QR2= PR× RS ⇢ 1
Apply the same for Δ PQR and Δ PSQ
PQ2= PR× PS ⇢ 2
From 1 and 2,
PQ2 + QR2= PR× RS + PR× PS
PQ2+ QR2= PR (RS+ PS)
PQ2+ QR2= PR2
Hence, Proved.
Sample Problems
Question 1: In the figure given below, XY is parallel to BC, AX=2cm, XB= 3cm, and the base of the triangle BC= 5cm, Then find the value of XY using Thales Theorem.

Solution:
According to Thales theorem,
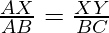
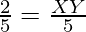
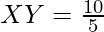
XY= 2cm
Question 2: In the right-angled triangle shown below, what is the value of p in terms of q.

Solution:
ABC is a right-angled triangle,
Using Pythagoras theorem, we get,
AC2= AB2+ BC2
P2= (4q)2+ (3q)2
P2= 16q+ 9q
p2= 25q
p= 5q
Question 3: In the below-given figure, when PQ is parallel to BC, find the value of x.

Solution:
In the Triangle, PQ is parallel to BC, therefore, Thales theorem can be applied,
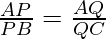

(3x-3)(2)= (x+2)(5)
6x-6= 5x+ 10
x = 16
Question 4: What are the three ways of proving the similarity of Two Triangles?
Answer:
The three ways of Proving Similarity of Triangles are:
- AAA similarity criterion (angle-angle-angle)
- SAS Similarity criterion (side- angle- side)
- SSS similarity criterion (side- side- side)
Question 5: In Triangle ABC, Line DE is drawn in such a way that ∠ABC = ∠DEC, Prove that ΔABC≅ ΔDEC.

Solution:
In ΔABC and ΔDEC,
It is already given that ∠ABC= ∠DEC
And since, angle C is common in both the Triangles, we can say,
∠ACB= ∠DCE
As two angles are equal, the third angle will automatically be equal since the sum of the three angles of a triangle is always 180°
Hence, from AAA Similarity Criterion, it can be concluded,
ΔABC ≅ ΔDEC
Question 6: In a Right-angled isosceles triangle, the base of the triangle is 2cm, Find the hypotenuse of the Triangle.
Solution:
The Triangle given in the question is a right-angled isosceles triangle and shall look something like this.

BC= 2cm
As it is an Isosceles triangle, AB= 2cm,
According to Pythagoras theorem, AC2= AB2 + BC2
AC2= 22+ 22
AC= √8 = 2√2cm
Question 7: How is SAS and SSS Criterion different from each other?
Answer:
Both Criteria have same result, that is, they both proved the triangles to be Congruent to each other, but the method of proving them is very different. In SSS criterion, when all the three sides are known to be equal, then the two Triangles are Congruent in nature. In SAS criterion, when any two sides and the angles between those two sides are equal, then the Triangles are known to be Congruent.
Share your thoughts in the comments
Please Login to comment...