Question 1. Give the geometric representations of y = 3 as an equation
(i) in one variable
(ii) in two variables
Solution:
(i) If y = 3 is treated as a equation in one variable y only, then it has the unique solution
y = 3, which is a point on the number line
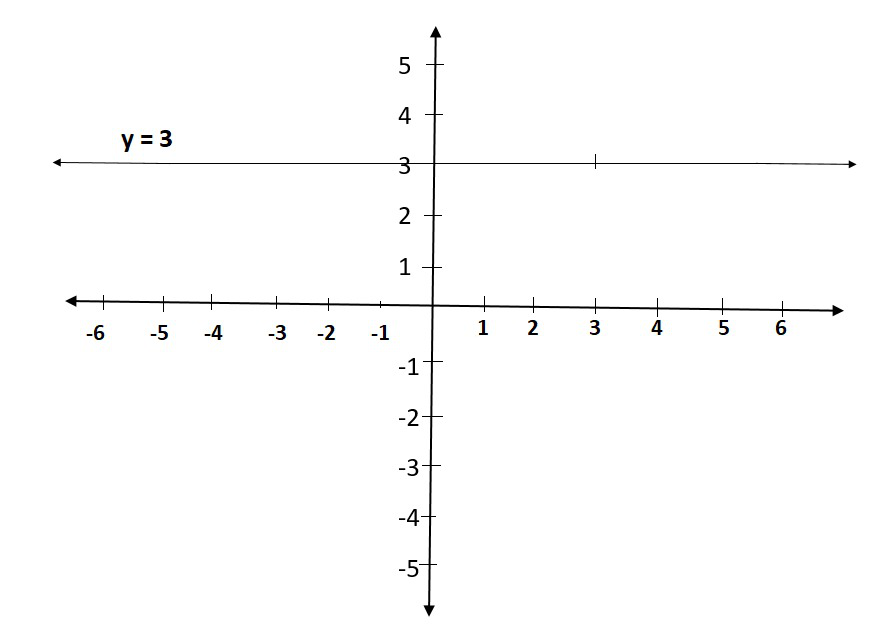
(ii) When an equation in two variables, it can be expressed as,
0.x + y – 3 = 0
which is a linear equation in the variables x and y. This is represented by a line. Now all the values of x are permissible because 0.x is always 0. However, y must satisfy the equation y = 3
This has infinitely many solutions. In fact, they are all of the form (r, 3), where r is any real number, so
We can have these two solutions for making line on a graph as:
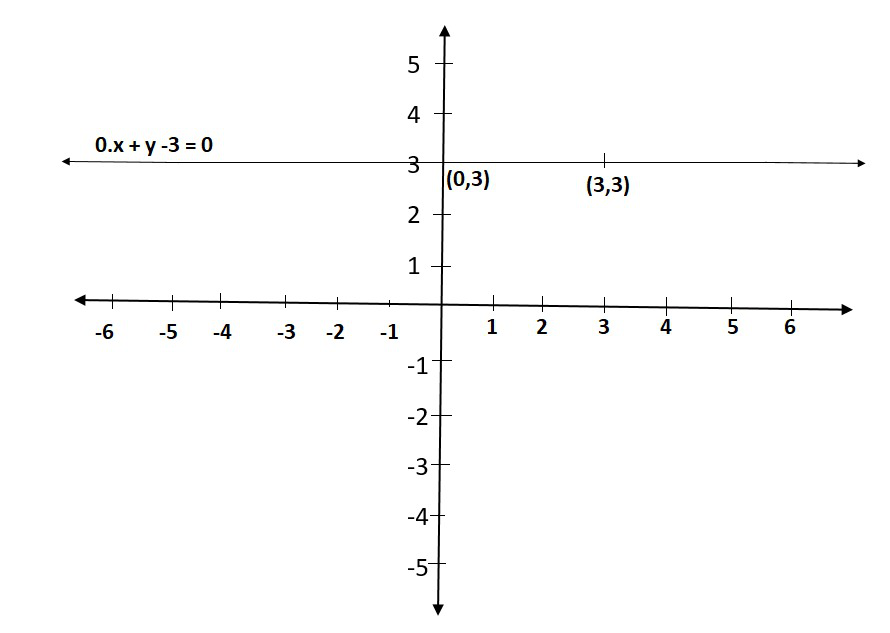
Question 2. Give the geometric representations of 2x + 9 = 0 as an equation
(i) in one variable
(ii) in two variables
Solution:
Firstly, we solve 2x + 9 = 0, to get
x = -9/2
(i) If x = -9/2 is treated as a equation in one variable x only, then it has the unique solution
x = -9/2, which is a point on the number line.
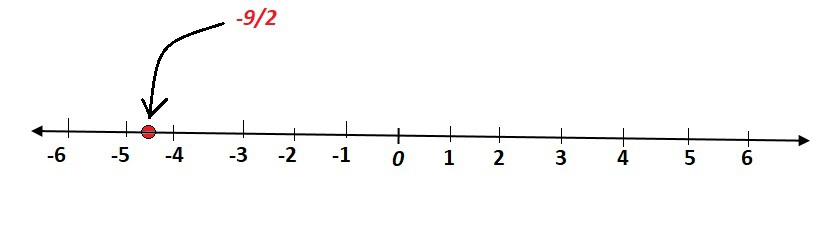
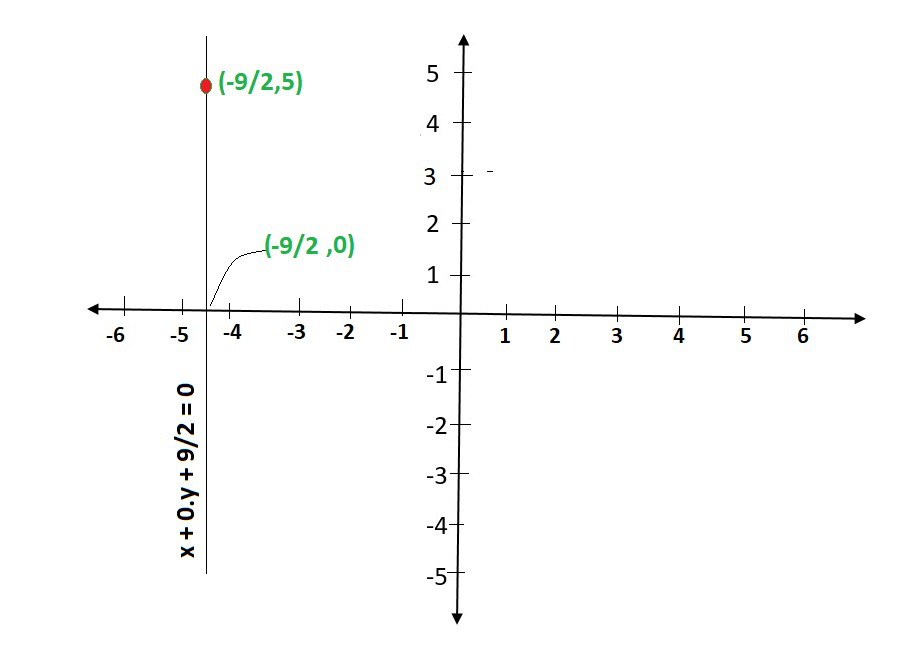
(ii) When an equation in two variables, it can be expressed as,
x + 0.y + 9/2 = 0
which is a linear equation in the variables x and y. This is represented by a line. Now all the values of y are permissible because 0.y is always 0. However, x must satisfy the equation x = -9/2
This has infinitely many solutions. In fact, they are all of the form (-9/2, r), where r is any real number, so
We can have these two solutions for making line on a graph as:
