Class 9 NCERT Solutions- Chapter 1 Number System – Exercise 1.3
Last Updated :
16 Mar, 2021
Question 1. Write the following in decimal form and say what kind of decimal expansion each has :
(i) 36/100
Solution:
In the given question, we get

Here, the remainder becomes zero.
Hence, decimal expansion becomes terminating.
36/100 = 0.36
(ii) 1/11
Solution:
In the given question, we get
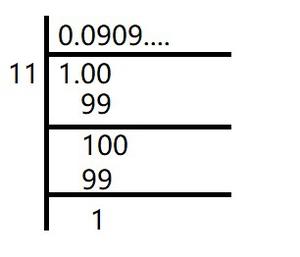
Here, the remainder never becomes zero and remainders repeat after a certain stage.
Hence, decimal expansion is non-terminating recurring
1/11 = 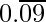
(iii) 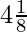
Solution:
Here, 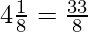
In the given question, we get

Here, the remainder becomes zero.
Hence, decimal expansion becomes terminating.
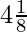 = 4.125
= 4.125
(iv) 3/13
Solution:
In the given question, we get

Here, the remainder never becomes zero and remainders repeat after a certain stage.
Hence, decimal expansion is non-terminating recurring
3/13 = 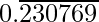
(v) 2/11
Solution:
In the given question, we get
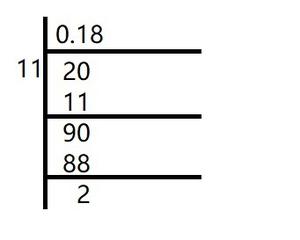
Here, the remainder never becomes zero and remainders repeat after a certain stage.
Hence, decimal expansion is non-terminating recurring
2/11 = 
(vi) 329/400
Solution:
In the given question, we get

Here, the remainder becomes zero.
Hence, decimal expansion becomes terminating.
329/400 = 0.8225
Question 2. You know that 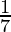 =
= 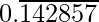 Can you predict what the decimal expansions of
Can you predict what the decimal expansions of 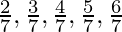 are, without actually doing the long division? If so, how?
are, without actually doing the long division? If so, how?
[Hint: Study the remainders while finding the value of 1/7 carefully.]
Solution:
As it is given,
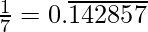
So,
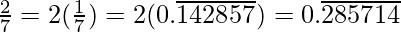
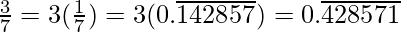
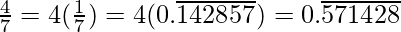
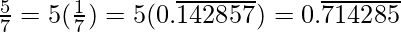
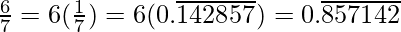
Question 3: Express the following in the form p/q, where p and q are integers and q ≠ 0.
(i) 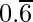
Solution:
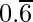 = 0.66666……
= 0.66666……
Lets’s take, x = 0.66666……
10x = 6.666….
So,
10x – x = (6.6666…..) – (0.66666……..)
9x = 6
x = 6/9
x = 2/3
Hence, x is in the form p/q, here p and q are integers and q ≠ 0.
(ii) 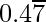
Solution:
 = 0.4777777……
= 0.4777777……
Lets’s take, x = 0.4777777……
10x = 4.77777…….
So,
10x – x = (4.77777…….) – (0.4777777……)
9x = 4.3
9x = 43/10
x = 43/90
Hence, x is in the form p/q, here p and q are integers and q ≠ 0.
(iii) 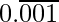
Solution:
 = 0.001001001……
= 0.001001001……
Lets’s take, x = 0.001001001……
1000x = 1.001001001……
So,
1000x – x = (1.001001001……) – (0.001001001……)
999x = 1
x = 1/999
Hence, x is in the form p/q, here p and q are integers and q ≠ 0.
Question 4. Express 0.99999 …. in the form p/q, Are you surprised by your answer? With your teacher and classmates discuss why the answer makes sense.
Solution:
Lets’s take, x = 0.99999……
10x = 9.99999….
So,
10x – x = (9.99999…..) – (0.99999……..)
9x = 9
x = 1
As, 0.9999….. just goes on, then at some point of time there is no gap between 1 and 0.9999….
We can observe that, 0.999 is too much near 1, hence, 1 is justified as the answer.
Hence, x is in the form p/q, where p and q are integers and q ≠ 0.
Question 5. What can the maximum number of digits be in the repeating block of digits in the decimal expansion of 1/17? Perform the division to check your answer.
Solution:
In the given question,
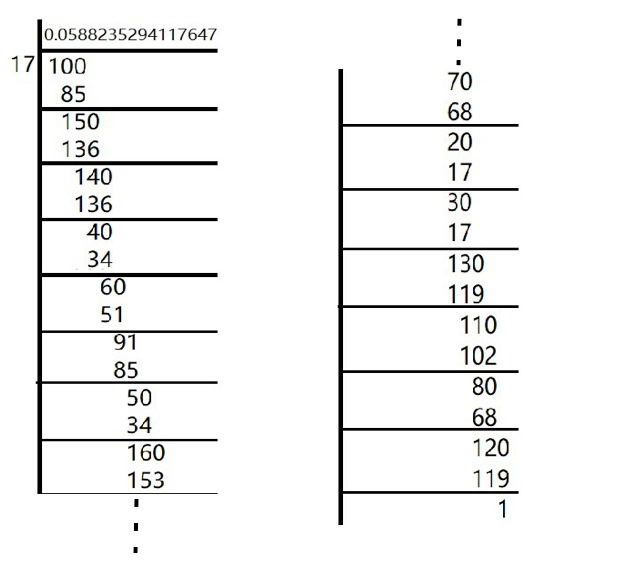
There are 16 digits in the repeating block of the decimal expansion of 1/17
Here, the remainder never becomes zero and remainders repeat after a certain stage.
Hence, decimal expansion is non-terminating recurring
1/17 = 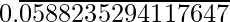
Question 6. Look at several examples of rational numbers in the form p/q (q ≠ 0), where p and q are integers with no common factors other than 1 and having terminating decimal representations (expansions). Can you guess what property q must satisfy?
Solution:
We observe that when q is 2, 4, 5, 8, 10… Then the decimal expansion is terminating.
Let’s take some example,
1/2 = 0. 5, denominator q = 21
7/8 = 0. 875, denominator q =23
4/5 = 0. 8, denominator q = 51
So, we conclude that terminating decimal may be obtained in the situation where
prime factorization of the denominator of the given fractions has the power
of only 2 or only 5 or both.
In the form of 2m × 5n, where n, m are natural numbers.
Question 7. Write three numbers whose decimal expansions are non-terminating non-recurring.
Solution:
As we know that all irrational numbers are non-terminating non-recurring.
So,
√5 = 2.23606798…….
√27 =5.19615242……
√41 = 6.40312424…..
Question 8. Find three different irrational numbers between the rational numbers 5/7 and 9/11.
Solution:
As, decimal expansion of
5/7 = 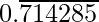
9/11 = 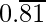
Hence, three different irrational numbers between them can be as follows,
0.73073007300073000073…
0.75075007300075000075…
0.76076007600076000076…
Question 9. Classify the following numbers as rational or irrational :
(i) √23
Solution:
√23 = 4.79583152……
As the number is non-terminating non-recurring.
It is an irrational number.
(ii) √225
Solution:
√225 = 15 = 15/1
As the number can be represented in p/q form, where q ≠ 0.
It is a rational number.
(iii) 0.3796
Solution:
As, the number 0.3796, is terminating.
It is a rational number.
(iv) 7.478478…
Solution:
As, the number 7.478478, is non-terminating but recurring.
It is a rational number.
(v) 1.101001000100001…
Solution:
As, the number 1.101001000100001…, is non-terminating but recurring.
It is a rational number.
Share your thoughts in the comments
Please Login to comment...