Class 9 NCERT Solutions- Chapter 13 Surface Areas And Volumes – Exercise 13.6
Last Updated :
10 Mar, 2021
Question 1. The circumference of the base of a cylindrical vessel is 132 cm and its height is 25 cm. How many liters of water can it hold? (1000 cm3 = 1l)
Solution:

Given values,
Circumference of the base of a cylindrical = 132 cm
Height of cylinder (h)= 25 cm
Base of cylinder is of circle shape, having circumference = 2πr (r is radius)
Hence, 2πr = 132 cm
r = 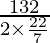 (taking π=
(taking π=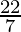 )
)
r =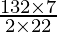
r = 21 cm
So, volume of cylinder = πr2h
= 22/7 × 21 × 21 × 25 (taking π=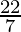 )
)
= 34650 cm3
As, 1000 cm3 = 1 litre
34650 cm3 = 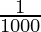 × 34650
× 34650
=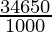
= 34.650 litres
Question 2. The inner diameter of a cylindrical wooden pipe is 24 cm and its outer diameter is 28 cm. The length of the pipe is 35 cm. Find the mass of the pipe, if 1 cm3 of wood has a mass of 0.6 g.
Solution:

Given values,
Inner radius of cylinder (r1)= 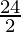 = 12 cm
= 12 cm
Outer radius of cylinder (r2)= 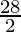 = 14 cm
= 14 cm
Height of cylinder (h)= 35 cm
So, volume used to make wood = volume of outer cylinder – volume of outer cylinder
= π(r22)h – π(r12)h
= π(r22 – r12)h
= 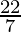 × (142 – 122) × 35 (taking π=
× (142 – 122) × 35 (taking π=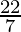 )
)
= 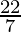 × (52) × 35
× (52) × 35
= 5720 cm3
As, 1 cm3 = 0.6 g
5720 cm3 = 0.6 × 5720 g
= 3432 grams
= 3.432 kg
Question 3. A soft drink is available in two packs –
(i) a tin can with a rectangular base of length 5 cm and width 4 cm, having a height of 15 cm and
(ii) a plastic cylinder with circular base of diameter 7 cm and height 10 cm.
Which container has greater capacity and by how much?
Solution:
Let’s see each case,
(i) The shape of can is cuboid here, as having rectangular base

Given values,
Length of can (l) = 5 cm
Width of can (b) = 4 cm
Height of can (h) = 15 cm
So, The amount of soft drink it can hold = volume of cuboid
= (l × b × h)
= 5 × 4 × 15 cm3
= 300 cm3
(ii)The shape of can is cylinder here, as having circular base

Given values,
Radius of can (r) = 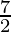 cm
cm
Height of can (h) = 10 cm
So, The amount of soft drink it can hold = volume of Cylinder
= (πr2h)
= 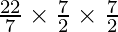 × 10 cm3 (taking π=
× 10 cm3 (taking π=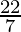 )
)
= 385 cm3
Hence, we can see the can having circular base can contain (385 – 300 = 85 cm3) more amount of soft drinks than first can.
Question 4. If the lateral surface of a cylinder is 94.2 cm2 and its height is 5 cm, then find
(i) radius of its base
(ii) its volume. (Use π = 3.14)
Solution:
Given values,

Lateral surface of cylinder = 94.2 cm2
Height of cylinder (h) = 5 cm
Let’s see each case,
(i) So, the lateral surface is of rectangle shape whose
length = (circumference of base circle of cylinder) and width = height of cylinder
Let the base radius = r
Lateral surface = length × width
94.2 cm2 = (2πr) × h (circumference of circle = 2πr)
94.2 cm2 = (2 × 3.14 × r) × 5 (taking π = 3.14)
r = 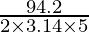
r = 3 cm
(ii) Given values,
Radius of cylinder (r)= 3 cm
So, the volume of cylinder = (πr2h)
= π × 3 × 3 × 5 cm3
= 3.14 × 3 × 3 × 5 cm3 (taking π = 3.14)
= 141.3 cm3
Question 5. It costs ₹2200 to paint the inner curved surface of a cylindrical vessel 10 m deep. If the cost of painting is at the rate of ₹20 per m2, find
(i) Inner curved surface area of the vessel,
(ii) Radius of the base,
(iii) Capacity of the vessel
Solution:
Given values,

Height of cylinder (h) = 10 m
Cost of painting rate = ₹20 per m2
Let’s see each case,
(i) For 1 m2 = ₹20
For lateral surface = ₹2200
So the lateral surface = 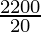
= 110 m2
(ii) Let the base radius = r
So as, Lateral surface = (circumference of base circle of cylinder) × height
110 m2= (2πr) × h
110 = (2 × 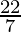 × r) × 10 (taking π=
× r) × 10 (taking π=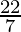 )
)
r = 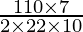 cm
cm
r = 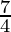 cm
cm
r = 1.75 cm
(iii) Volume of cylinder = (πr2h)
= 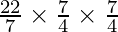 × 10 cm3 (taking π=
× 10 cm3 (taking π=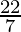 )
)
= 96.25 cm3
Question 6. The capacity of a closed cylindrical vessel of height 1 m is 15.4 liters. How many square meters of metal sheet would be needed to make it?
Solution:
Given values,

Height of cylinder (h) = 1 m = 100 cm
Volume of cylinder (V) = 15.4 liters
As 1 liter = 1000 cm3
15.4 liters = 15.4 × 1000 cm3
V = 15,400 cm3
Volume of cylinder = (πr2h)
15,400 = 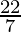 × r2 × 100 (taking π=
× r2 × 100 (taking π=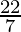 )
)
r2 = 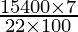
r2 = 49
r = √49
r = 7 cm
Surface area of a closed cylinder = (curve surface area + top and bottom circle) = 2πrh + (2 × πr2)
= 2πr (r+h)
= 2 × 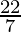 × 7 × (7 + 100) cm2 (taking π=
× 7 × (7 + 100) cm2 (taking π=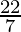 )
)
= 2 × 22 × 107
= 4708 cm2
= 0.4708 m2
Hence, 0.4708 m2 of metal sheet would be needed to make it.
Question 7. A lead pencil consists of a cylinder of wood with a solid cylinder of graphite filled in the interior. The diameter of the pencil is 7 mm and the diameter of the graphite is 1 mm. If the length of the pencil is 14 cm, find the volume of the wood and that of the graphite.
Solution:
So here pencil = (cylinder of wood + cylinder of graphite)
Given values,

Height of wood (and graphite) cylinder (h) = 14 cm = 140 mm
Radius of pencil (R)= 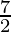 mm
mm
Radius of graphite (r)= 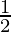 mm
mm
Volume of Graphite = (πr2h)
= 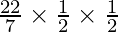 × 140 mm3 (taking π=
× 140 mm3 (taking π=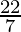 )
)
= 110 mm3
= 0.11 cm3
Volume of wood = Volume of pencil – Volume of graphite
= (πR2h) – (πr2h) = π(R2 – r2)h
= 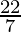 × ((
× ((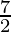 )2 – (
)2 – (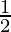 )2) × 140 mm3 (taking π=
)2) × 140 mm3 (taking π=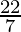 )
)
= 22 × 20 × (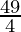 –
– 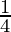 ) mm3
) mm3
= 22 × 20 × 12 mm3
= 5280 mm3
= 52.80cm3
Question 8. A patient in a hospital is given soup daily in a cylindrical bowl of diameter 7 cm. If the bowl is filled with soup to a height of 4 cm, how much soup the hospital has to prepare daily to serve 250 patients?
Solution:
So here Volume of soup for each patient = Volume of cylinder.
Given values,

Height of cylinder (h) = 4 cm
Radius of cylinder (r)= 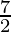 cm
cm
Volume of Cylinder = (πr2h)
= 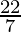 ×
×  × 4 cm3 (taking π=
× 4 cm3 (taking π=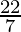 )
)
= 154 cm3
Volume of soup for 250 patient = 250 × Volume of cylinder.
= 250 × 154
= 38,500 cm3
Hence, 38,500cm3 soup is needed daily to serve 250 patients.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...