Class 9 NCERT Solutions- Chapter 7 Triangles – Exercise 7.3
Last Updated :
03 Jan, 2021
Question 1. ΔABC and ΔDBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC (see Figure). If AD is extended to intersect BC at P, show that
(i) ΔABD ≅ ΔACD
(ii) ΔABP ≅ ΔACP
(iii) AP bisects ∠A as well as ∠D.
(iv) AP is the perpendicular bisector of BC.
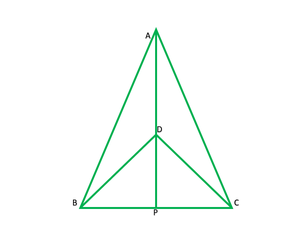
Solution:
Given: ∆ABC and ∆DCB are isosceles ∆on the same base BC.
To show:
- ΔABD ≅ ΔACD
- ΔABP ≅ ΔACP
- AP bisects ∠A as well as ∠D.
- AP is the perpendicular bisector of BC.
i) in ∆ABD and ∆ACB
AB=AC
BD=CD
AD=AD
∆ABD≅∆ACD ————-(S.S.S)
ii) in ∆ABP and ∆ACP
AB=AC
∠ BAP≅∠CAP [∆ABD≅∆ACD BY C.P.CT]
AP=AP ———[common]
∴[∆ABD≅∆ACD ———–[S.A.S]
iii) [∆ABD≅∆ACD ———–[S.A.S]
∠BAD=∠CAD
AD, bisects ∠A
AP, bisects ∠A —————–1
In ∆ BDP and ∆DPB
BD=CD —————(GIVEN)
DP=PC ———-[∆AB≅ ∆ACP C.P.C.T]
DP=DP ———–[common]
∴∆BDP≅∆CDP (S.S.S)
∠BDP=∠CDP (C.P.C.T)
DP bisects ∠D
AP bisects ∠D ——————-2
From 1 and 2, AP bisects ∠ A as well as ∠ D
iv) ∠ AP +∠APC =180° ————[linear pair]
∠APB=∠APC ————-[∆ABP≅∆ACP C.P.CT]
∠APB + ∠APC=180°
2 ∠ APB=180°
∠APB=180/2=90°
BP=PC (FROM ii)
∴AP is ⊥ bisects of BC.
Question 2. AD is an altitude of an isosceles triangle ABC in which AB = AC. Show that
(i) AD bisects BC (ii) AD bisects ∠A.
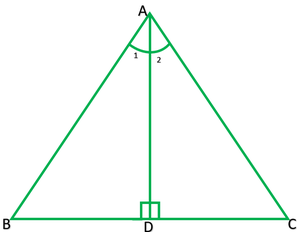
Solution:
Given: AB=AC, AD altitude
To Show:
(i) AD bisects BC (ii) AD bisects ∠A.
In ∆ADB and ∆ADC
∠ADB=∠ADC ——– ———–[each 90°] R
AB=AC ——————–[given]S
AD=AD ——–[common]S
∴ ∆ADB ≅∆ADC
BD=DC ————-[c.p.c.t]
∴AD bisects BC
∠1=∠2 ————-[c.p.c.t]
∴AD bisects ∠A
Question 3. Two sides AB and BC and median AM of one triangle ABC are respectively equal to sides PQ and QR and median PN of ΔPQR (see Fig. 7.40). Show that:
(i) ΔABM ≅ ΔPQN
(ii) ΔABC ≅ PQR
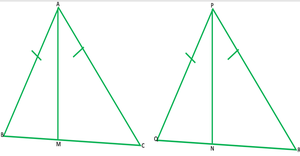
Solution:
Given:
AB=PQ
BC=QR
AM=PN
AM and PN are medians
To show:(i) ΔABM ≅ ΔPQN (ii) ΔABC ≅ PQR
Solution: In ΔABM and ΔPQN
AB=PQ
AM=PN
because AM and PN are medians BC=QR
therefore =1/2BC=1/2QR
∴BM=QN
∴) ΔABM ≅ ΔPQN ———[S.S.S]
∠B=∠Q ——–[c.p.c.t]
ii)now in ΔABC and ΔPQR
AB=PQ ———-[given]
∠B=∠Q from (i)
BC=QR —————-[given]
∴ ΔABC ≅ PQR [S.A.S]
Question 4. BE and CF are two equal altitudes of a triangle ABC. Using RHS congruence rule, prove that the triangle ABC is isosceles.
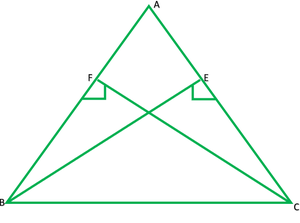
Solution:
Given: altitude BE and CF are equal
To prove: ΔABC is an isosceles Δ
In ΔBEC and ΔCEB
∠E=∠F —————-[each 90°] R
BC=BC —————–[common] H
BF=CF —————-[given] S
# ΔBEC ≅ ΔCEB [R.H.S]
∠C=∠B ————-[C.P.C.T]
In ΔABC,
∠C=∠B
Question 5. ABC is an isosceles triangle with AB = AC. Draw AP ⊥ BC to show that ∠B = ∠C.
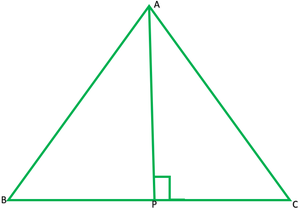
Solution:
Given:
In ∆ABC,
AB=BC
AP ⊥ BC
to show that: ∠B = ∠C.
Solution:
In ∆APB and ∆APC
∠APB = ∠APC —————[ each 90°] R
AB=AC ——————-[given] H
AP=AP ——————–[common] S
∴∆APB ≅ ∆APC ———-[R.H.S]
∠B = ∠C —————[C.P.C.T]
Share your thoughts in the comments
Please Login to comment...