Question 1. In Figure, E is any point on median AD of a ΔABC. Show that ar (ABE) = ar(ACE).
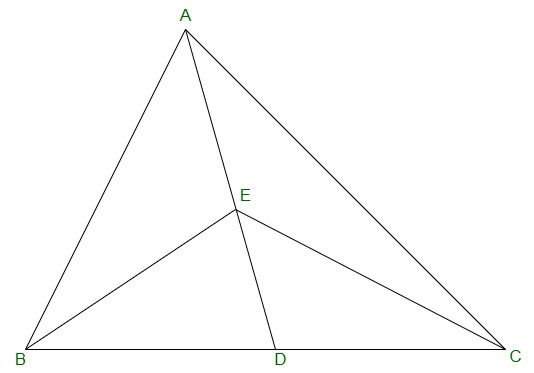
Solution:
Given:
AD is median of ΔABC.
Therefore,
It will divide ΔABC into two triangles of equal area.
Therefore,
ar(ABD) = ar(ACD) -(equation 1)
also,
ED is the median of ΔABC.
Therefore,
ar(EBD) = ar(ECD) -(equation 2)
Subtracting equation (2) from (1),
ar(ABD) – ar(EBD) = ar(ACD) – ar(ECD)
=> ar(ABE) = ar(ACE)
Question 2. In a triangle ABC, E is the mid-point of median AD. Show that ar(BED) = 1/4 ar(ABC).
Solution:
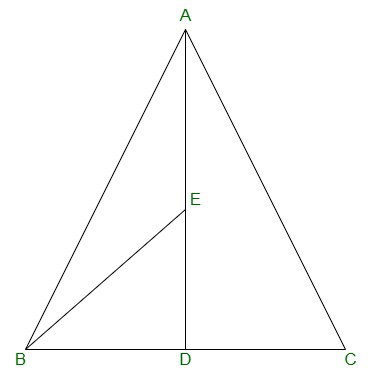
ar(BED) = (1/2)×BD×DE
Thus,
E is the mid-point of AD,
AE = DE
Thus,
AD is the median on side BC of triangle ABC,
BD = DC
DE = (1/2) AD -(equation 1)
BD = (1/2)BC -(equation-2)
From equation (1) and (2), we get,
ar(BED) = (1/2) × (1/2)BC × (1/2)AD
=> ar(BED) = (1/2) × (1/2)ar(ABC)
=> ar(BED) = 1/4 ar(ABC)
Question 3. Show that the diagonals of a parallelogram divide it into four triangles of equal area.
Solution:
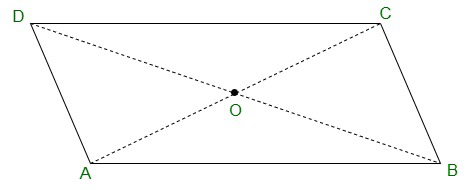
O is the mid point of AC and BD. (as diagonals bisect each other)
In ΔABC, BO is the median.
Therefore,
ar(AOB) = ar(BOC) -(equation 1)
also,
In ΔBCD, CO is the median.
Therefore,
ar(BOC) = ar(COD) -(equation 2)
In ΔACD, OD is the median.
Therefore,
ar(AOD) = ar(COD) -(equation 3)
In ΔABD, AO is the median.
Therefore,
ar(AOD) = ar(AOB). -(equation4)
From equations (1), (2), (3) and (4), we have,
ar(BOC) = ar(COD) = ar(AOD) = ar(AOB)
Therefore,
we get, the diagonals of a parallelogram divide it into four triangles of equal area.
Question 4. In Figure, ABC and ABD are two triangles on the same base AB. If line- segment CD is bisected by AB at O, show that: ar(ABC) = ar(ABD).
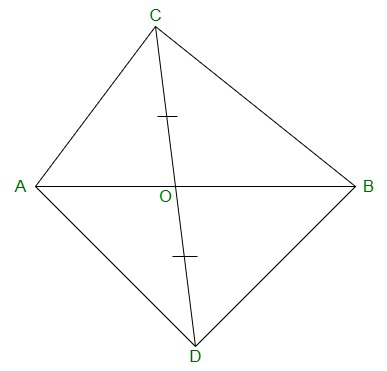
Solution:
In ΔABC, AO is the median. (CD is bisected by AB at O)
Therefore,
ar(AOC) = ar(AOD) -(equation 1)
also,
ΔBCD, BO is the median. (CD is bisected by AB at O)
Therefore,
ar(BOC) = ar(BOD) -(equation 2)
Adding equation (1) and (2),
We will get,
ar(AOC)+ar(BOC) = ar(AOD)+ar(BOD)
=> ar(ABC) = ar(ABD)
Question 5. D, E and F are respectively the mid-points of the sides BC, CA, and AB of a ΔABC. Show that
(i) BDEF is a parallelogram.
(ii) ar(DEF) = 1/4 ar(ABC)
(iii) ar (BDEF) = 1/2 ar(ABC)
Solution:
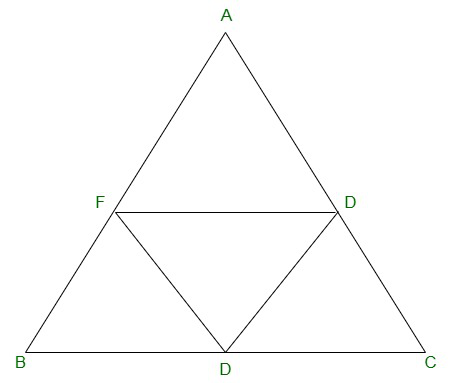
(i) In ΔABC,
EF || BC and EF = 1/2 BC (by mid point theorem)
also,
BD = 1/2 BC (D is the mid point)
So,
BD = EF
also,
BF and DE are parallel and equal to each other.
Therefore,
The pair opposite sides are equal in length and parallel to each other.
Hence, BDEF is a parallelogram.
(ii) Proceeding from the result of (i),
BDEF, DCEF, AFDE are parallelograms.
Diagonal of a parallelogram divides it into two triangles of equal area.
Therefore,
ar(ΔBFD) = ar(ΔDEF) (For parallelogram BDEF) -(equation 1)
also,
ar(ΔAFE) = ar(ΔDEF) (For parallelogram DCEF) -(equation 2)
ar(ΔCDE) = ar(ΔDEF) (For parallelogram AFDE) -(equation 3)
From equations (1), (2) and (3)
ar(ΔBFD) = ar(ΔAFE) = ar(ΔCDE) = ar(ΔDEF)
=> ar(ΔBFD) + ar(ΔAFE) + ar(ΔCDE) + ar(ΔDEF) = ar(ΔABC)
=> 4 ar(ΔDEF) = ar(ΔABC)
=> ar(DEF) = 1/4 ar(ABC)
(iii) Area (parallelogram BDEF) = ar(ΔDEF) + ar(ΔBDE)
=> ar(parallelogram BDEF) = ar(ΔDEF) + ar(ΔDEF)
=> ar(parallelogram BDEF) = 2× ar(ΔDEF)
=> ar(parallelogram BDEF) = 2× 1/4 ar(ΔABC)
=> ar(parallelogram BDEF) = 1/2 ar(ΔABC)
Question 6. In Figure, diagonals AC and BD of quadrilateral ABCD intersect at O such that OB = OD.
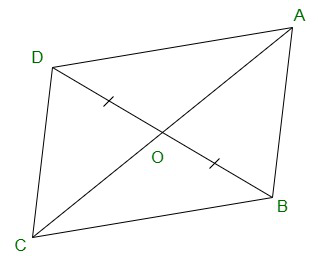
If AB = CD, then show that:
(i) ar (DOC) = ar (AOB)
(ii) ar (DCB) = ar (ACB)
(iii) DA || CB or ABCD is a parallelogram.
[Hint : From D and B, draw perpendiculars to AC.]
Solution:
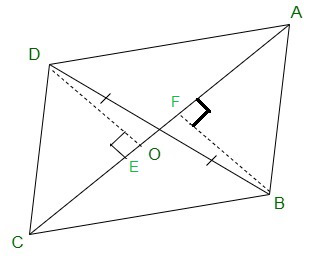
Given:
OB = OD and AB = CD
Construct,
DE ⊥ AC and BF ⊥ AC.
To proof:
(i) In ΔDOE and ΔBOF,
∠DEO = ∠BFO (Perpendiculars)
∠DOE = ∠BOF (Vertically opposite angles)
OD = OB (Given)
Therefore,
ΔDOE ≅ ΔBOF by AAS congruence condition.
Therefore, DE = BF (By CPCT) -(equation 1)
also,
ar(ΔDOE) = ar(ΔBOF) (Congruent triangles) -(equation 2)
Now,
In ΔDEC and ΔBFA,
∠DEC = ∠BFA (as they are perpendiculars)
CD = AB (Given)
DE = BF (From equation 1)
Therefore,
ΔDEC ≅ ΔBFA by RHS congruence condition.
Therefore,
ar(ΔDEC) = ar(ΔBFA) (Congruent triangles) -(equation 3)
Adding equation (2) and (3),
ar(ΔDOE) + ar(ΔDEC) = ar(ΔBOF) + ar(ΔBFA)
=> ar (DOC) = ar (AOB)
(ii) ar(ΔDOC) = ar(ΔAOB)
Adding ar(ΔOCB) in LHS and RHS,
we will get,
=> ar(ΔDOC) + ar(ΔOCB) = ar(ΔAOB) + ar(ΔOCB)
=> ar(ΔDCB) = ar(ΔACB)
(iii) When two triangles have same base and equal areas,
the triangles will be in between the same parallel lines
ar(ΔDCB) = ar(ΔACB)
DA || BC -(equation 4)
For quadrilateral ABCD, one pair of opposite sides are
equal (AB = CD) and other pair of opposite sides are parallel.
Therefore,
ABCD is parallelogram.
Question 7. D and E are points on sides AB and AC, respectively of ΔABC such that ar(DBC) = ar(EBC). Prove that DE || BC.
Solution:
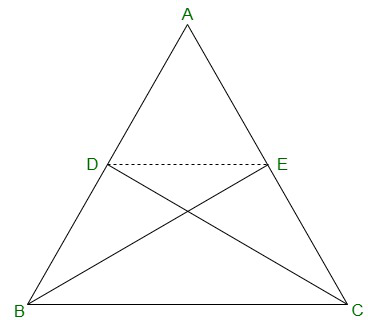
ΔDBC and ΔEBC are on the same base BC and are having equal areas.
Therefore,
They will lie between the same parallel lines.
Therefore,
DE || BC.
Question 8. XY is a line parallel to side BC of a triangle ABC. If BE || AC and CF || AB meet XY at E and F respectively, show that ar(ΔABE) = ar(ΔACF)
Solution:
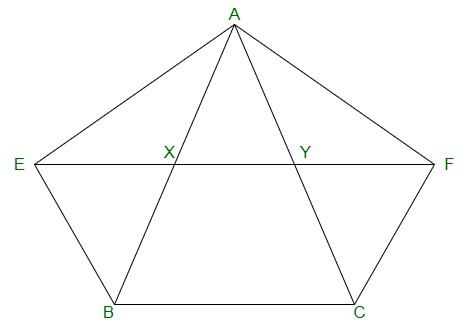
Given,
XY || BC, BE || AC and CF || AB
We have to show that,
ar(ΔABE) = ar(ΔAC)
Proof:
BCYE is a parallelogram as ΔABE and ||gm BCYE are on the same
base BE and between the same parallel lines BE and AC.
Therefore,
ar(ABE) = 1/2 ar(BCYE) -(equation 1)
Now,
CF || AB and XY || BC
=> CF || AB and XF || BC
=> BCFX is a parallelogram.
Thus ΔACF and parallelogram BCFX are on the same base CF
and in-between the same parallel AB and FC. Therefore,
ar (ΔACF)= 1/2 ar (BCFX) -(equation 2)
But,
Parallelogram BCFX and parallelogram BCYE are on the same
base BC and between the same parallels BC and EF. Therefore,
ar (BCFX) = ar(BCYE) -(equation 3)
From equations (1), (2) and (3),
We will get,
ar (ΔABE) = ar(ΔACF)
=> ar(BEYC) = ar(BXFC)
As the parallelograms are on the same base BC and
in-between the same parallels EF and BC -(equation 3)
Also,
ΔAEB and parallelogram BEYC are on the same base
BE and in-between the same parallels BE and AC.
=> ar(ΔAEB) = 1/2 ar(BEYC) -(equation 4)
Similarly,
ΔACF and parallelogram BXFC on the same base CF
and between the same parallels CF and AB.
=> ar(ΔACF) = 1/2 ar(BXFC) -(equation 5)
From equations (3), (4) and (5),
ar(ΔABE) = ar(ΔACF).
Question 9. The side AB of a parallelogram ABCD is produced to any point P. A line through A and parallel to CP meets CB produced at Q and then parallelogram PBQR is completed (see Figure). Show that
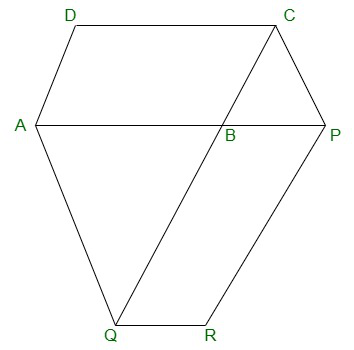
ar(ABCD) = ar(PBQR).
[Hint : Join AC and PQ. Now compare ar(ACQ) and ar(APQ).]
Solution:
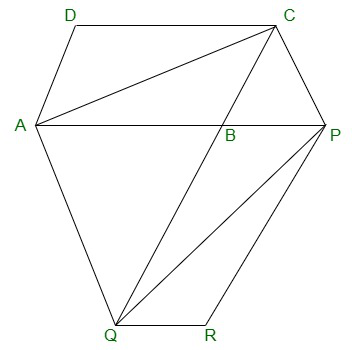
AC and PQ are joined.
Ar(ΔACQ) = ar(ΔAPQ)(On the same base AQ and between
the same parallel lines AQ and CP)
=> ar(ΔACQ)-ar(ΔABQ) = ar(ΔAPQ)-ar(ΔABQ)
=> ar(△ABC) = ar(△QBP) -(equation 1)
AC and QP are diagonals ABCD and PBQR.
Therefore,
ar(ABC) = 1/2ar(ABCD) -(equation 2)
ar(QBP) = 1/2 ar(PBQR) -(equation 3)
From equation (2) and (3),
1/2 ar(ABCD) = 1/2 ar(PBQR)
=> ar(ABCD) = ar(PBQR)
Question 10. Diagonals AC and BD of a trapezium ABCD with AB || DC intersect each other at O. Prove that ar (AOD) = ar (BOC).
Solution:
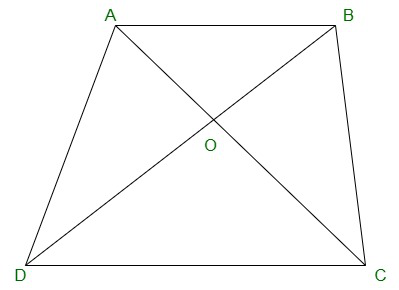
ΔDAC and ΔDBC lie on the same base DC and
between the same parallels AB and CD.
Ar(ΔDAC) = ar(ΔDBC)
=> ar(ΔDAC) – ar(ΔDOC) = ar(ΔDBC) – ar(ΔDOC)
=> ar(ΔAOD) = ar(ΔBOC)
Share your thoughts in the comments
Please Login to comment...