Class 9 NCERT Solutions – Chapter 10 Circles – Exercise 10.3
Last Updated :
05 Jan, 2023
Question 1. Draw different pairs of circles. How many points does each pair have in common? What is the maximum number of common points?
Solution:
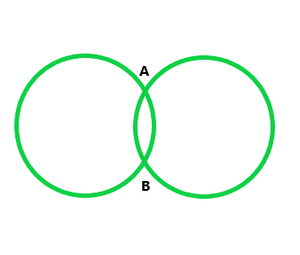
(i) Two points common
(ii) One point common
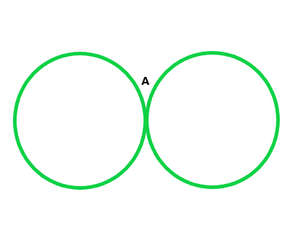
(iii) One point common

(iv) No point common

(v) No point common

As we can analyse from above, two circles can cut each other maximum at two points.
Question 2. Suppose you are given a circle. Give a construction to find its centre.
Solution:
Let the circle be C1
We need to find its centre.
Step 1: Take points P, Q, R on the circle
Step 2: Join PR and RQ.
We know that perpendicular bisector of a chord passes through centre
So, we construct perpendicular bisectors of PR and RQ
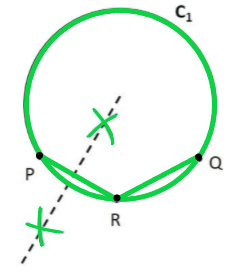
Step 3: Take a compass. With point P as pointy end and R as pencil end of the compass, mark an arc above and below PR. Do same with R as pointy end P as pencil end of the compass.
Step 4: Join points intersected by the arcs.
The line formed is the perpendicular bisector of PR.
Step 5: Take compass, with point R as pointy end and Q as pencil end of the compass mark an arc above and below RQ.
Do the same with Q as pointy end and R as pencil end of the compass
Step 6: Join the points intersected by the arcs.
The line formed is the perpendicular bisector of RQ.
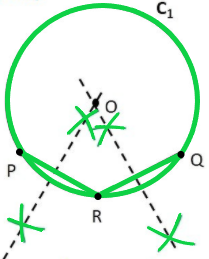
Step 7: The point where two perpendicular bisectors intersect is the centre of the circle. Mark it as point O.
Thus, O is the centre of the given circle.
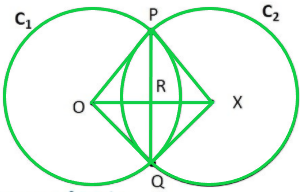
Question 3: If two circles intersect at two points, prove that their centres lie on the perpendicular bisector of the common chord.
Solution:
Given,
Let circle C1 have centre O and circle C2 have centre X, PQ is the common chord.
To prove: OX is the perpendicular bisector of PQ i.e.
1. PR = RQ
2. ∠PRO = ∠PRX = ∠QRO = ∠QRX = 90°
Construction:
Join PO, PX, QO, QX
Proof:
In △POX and △QOX
OP = OQ (Radius of circle C1)
XP = XQ (Radius of circle C2)
OX = OX (Common)
∴ △POX ≅ △QOX (SSS Congruence rule)
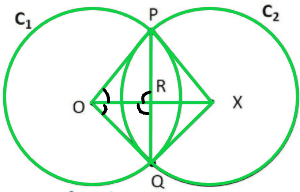
∠POX = ∠QOX (CPCT) —-(1)
Also,
In △POR and △QOR
OP = OQ (Radius of circle C1)
∠POR = ∠QOR ( From (1))
OR = OR (Common)
∴ △OPX ≅ △OQX (SAS Congruence Rule)
PR = QR (CPCT)
& ∠PRO = ∠QRO (CPCT) —-(2)
Since PQ is a line
∠PRO + ∠QRO = 180° (Linear Pair)
∠PRO + ∠PRO= 180° ( From (2))
2∠PRO = 180°
∠PRO = 180° / 2
∠PRO = 90°
Therefore,
∠QRO = ∠PRO = 90°
Also,
∠PRX = ∠QRO = 90° (Vertically opposite angles)
∠QRX = ∠PRO = 90° (Vertically opposite angles)
Since, ∠PRO = ∠PRX = ∠QRO = ∠QRX = 90°
∴ OX is the perpendicular bisector of PQ
Share your thoughts in the comments
Please Login to comment...