Class 9 NCERT Solutions – Chapter 1 Number System – Exercise 1.2
Last Updated :
12 Mar, 2021
Question 1: State whether the following statements are true or false. Justify your answers.
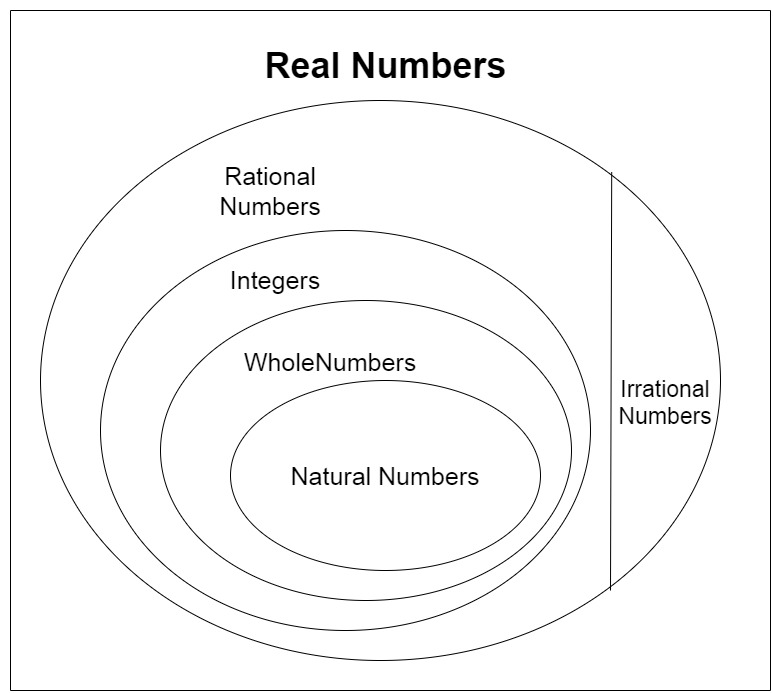
(i) Every irrational number is a real number.
(ii) Every point on the number line is of the form √m , where m is a natural number.
(iii) Every real number is an irrational number.
Solution:
(i) Every irrational number is a real number.
True
Irrational numbers are the number that cannot be written in the form of p/q , p and q are the integers and q ≠ 0.
Some examples of irrational numbers are π, √3, e, √2, 011011011…..
Real numbers include both rational numbers and irrational numbers.
Thus, every irrational number is a real number.
(ii) Every point on the number line is of the form √m, where m is a natural number.
False
We can represent both negative and positive numbers on a number line.
Positive numbers can be written as √16=4 that is a natural number, But √3=1.73205080757 is not a natural number.
But negative numbers cannot be expressed as the square root of any natural number, as if we take square root of an negative number it will become complex number that will not be a natural number (√5=5i is a complex number).
(iii) Every real number is an irrational number.
False
Every irrational number is a real number but every real number is not an irrational number as real numbers include both rational and irrational number.
Question 2: Are the square roots of all positive integers irrational? If not, give an example of the square root of a number that is a rational number.
Solution:
No, the square roots of all positive integers in not irrational. For example √9 = 3, √25 = 5, hence square roots of all positive integers is not irrational.
Question 3: Show how √5 can be represented on the number line.
Solution:
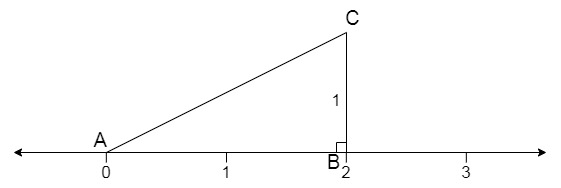
To represent √5 on the number line follow the following steps:
Step 1: Draw a number line.
Step 2: Let line AB of 2 units on the number line.
Step 3: Now draw a perpendicular of unit 1 on point B and mark the other end as point C.
Step 4: Join AC, you will have triangle ABC which is a right-angle triangle. as shown below:
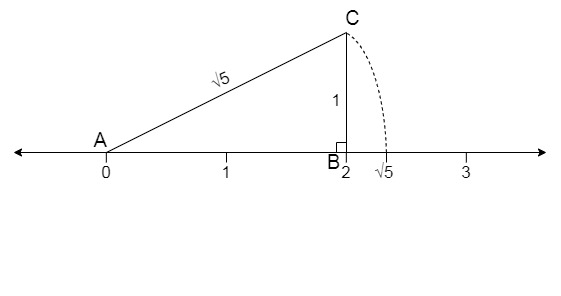
Step 5: Apply Pythagoras Theorem on triangle ABC,
⇒ AB2 + BC2 = AC2
⇒ AC2 = 22 + 12
⇒ AC2 = 5
⇒ AC = √5
Therefore, line AC is of √5 unit length.
Step 6: Now take line AC as the radius and an arc and intersect it to number line, the point where the arc will intersect the number line is of lengths √5 from point 0 to the intersection as point A is the centre of the radius.
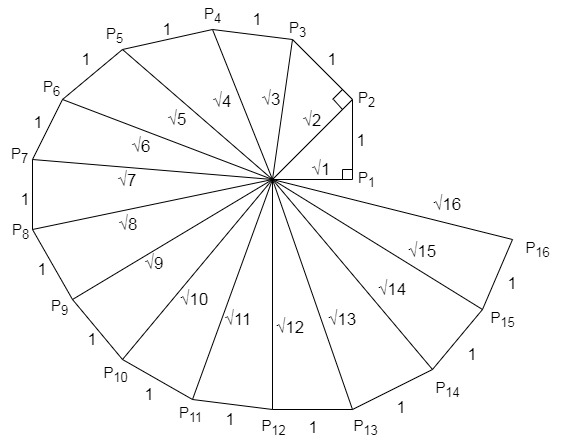
Question 4: Classroom activity (Constructing the ‘square root spiral’): Take a large sheet of paper and construct the ‘square root spiral’ in the following fashion. Start with a point O and draw a line segment OP1 of unit length. Draw a line segment P1 P2 perpendicular to OP1 of unit length (see Fig. 1.9). Now draw a line segment P2 P3 perpendicular to OP2. Then draw a line segment P3 P4 perpendicular to OP3. Continuing in this manner, you can get the line segment Pn-1Pn by drawing a line segment of unit length perpendicular to OPn-1. In this manner, you will have created the points P2, P3, …., Pn, …., and joined them to create a beautiful spiral depicting √2, √3, √4, …
Solution:
Step 1: First lets mark a point O on the larger sheet of paper, this point will be the centre of the square root spiral.
Step 2: Draw point P1 from point O of 1 unit. OP1=1 unit.
Step 3: Similarly as in the above problem from P1 draw a perpendicular of 1 unit, P1P2 = 1 unit.
Step 4: Now join OP2 = √2
Step 5: From point P2 draw a perpendicular of 1 unit. P2P3 = 1 unit.
Step 6: Now join OP3 = √3
Step 7: Now repeat the step to make √4, √5, √6, …….
Share your thoughts in the comments
Please Login to comment...