NCERT Solutions for Class 10 Maths Chapter 8 Introduction to Trigonometry

NCERT Solutions for Class 10 Maths Chapter 8 Introduction to Trigonometry – This article includes detailed NCERT Solutions for Class 10 Maths Chapter 8 Introduction to Trigonometry, designed and reviewed by subject experts at GFG.

NCERT Class 10 Maths Chapter 8 Introduction to Trigonometry comprises the following topics:

• Introduction to Trigonometry
• Trigonometric identities
• Trigonometric ratios of complementary angles

Class 10 Maths NCERT Solutions Chapter 8 Introduction to Trigonometry Exercises
NCERT Solutions for Class 10 Maths Chapter 8 Introduction to Trigonometry Exercise 8.1 – 11 Questions (8 Short Answers, 3 Long Answers)
NCERT Solutions for Class 10 Maths Chapter 8 Introduction to Trigonometry Exercise 8.2 – 4 Questions (2 Short Answers, 2 Long Answers)
NCERT Solutions for Class 10 Maths Chapter 8 Introduction to Trigonometry Exercise 8.3 – 7 Questions (5 Short Answers, 2 Long Answers)
NCERT Solutions for Class 10 Maths Chapter 8 Introduction to Trigonometry Exercise 8.4 – 5 Questions (3 Short Answers, 2 Long Answers)

This article provides solutions to all the problems asked in Class 10 Maths Chapter 8 Introduction to Trigonometry of your NCERT textbook in a step-by-step manner. Solutions to all the exercises in the NCERT Class 9 Maths Chapter 7 Triangles are regularly revised to check errors and updated according to the latest CBSE Syllabus 2023-24 and guidelines.

The solutions to all the ercercises in NCERT Chapter 8 Introduction to Trigonometry have been collectively covered in NCERT Solutions for Class 10 Maths.

NCERT Solutions for Class 10 Maths Chapter 8 Introduction to Trigonometry: Exercise 8.1

Question 1. In ∆ ABC, right-angled at B, AB = 24 cm, BC = 7 cm. Determine:

(i) sin A, cos A (ii) sin C, cos C

Solution:

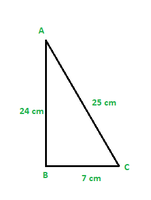
Using Pythagoras theorem for ΔABC

AC² = AB² + BC²

= (24 cm)² + (7 cm)²

= (576 + 49) cm²

= 625 cm²

∴AC = 25 cm       

(i) sin A = opp/hyp

    sin A = 7/25

    cos A = adj/hyp = 24/25

    cos A = 24/25

(ii) sin C = opp/hyp

     sin C = 24/25

     cos C = adj/hyp

     cos C = 7/25

Question 2. In Fig., find tan P – cot R.

Solution:

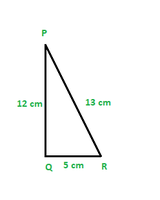
Applying Pythagoras theorem for ΔPQR, we obtain

PR² = PQ² + QR²

(13 cm)² = (12 cm)² + QR²

169 cm² = 144 cm² + QR²

25 cm² = QR²

QR = 5 cm

tan P = opp/adj

tan P = 5/12

cot R = adj/opp

cot R = 5/12

tan P – cot R = 5/12 – 5/12 = 0

Question 3. If sin A = 3/4, calculate cos A and tan A.

Solution:

Using sin²A + cos²A = 1

(3/4)² + cos²A = 1

cos²A = 1 – (3/4)² = 1 – 9/16

cos A = 7^1/2/4

tan A = sin A/cos A

tan A = (3/4)/(7^1/2/4)

tan A = 3/7^1/2

Question 4: Given 15 cot A = 8. Find sin A and sec A

Solution:

Given, 15 cot A = 8

               cot A = 8/15

tan A = 1/cot A

tan A = 15/8

Using, 1 + tan²A = sec²A

           1 + (15/8)² = sec²A

           289/64 = sec²A

           sec A = 17/8

We know, cos²A = 1/sec²A

                cos²A = 64/289

               sin²A = 1 – cos2A

               sin²A = 225/289

 sin A = 15/17

Question 5: Given sec θ = 13/12, calculate all other trigonometric ratios.

Solution.

Using Pythagoras theorem,

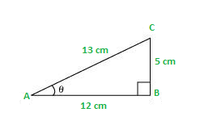
sin θ = 5/13

cos θ = 12/13

tan θ = 5/12

cosec θ = 13/5

cot θ = 12/5

Question 6: If ∠A and ∠B are acute angles such that cos A = cos B, then show that ∠A = ∠B.

Solution:

Let us consider a ΔABC in which CD ⊥ AB.

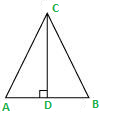
It is given that cos A = cos B

AD/AC = BD/BC     … (1)

We need to prove ∠A = ∠B. To prove this, we need to extend AC to P such that BC = CP.

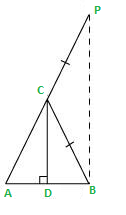
From equation (1), we obtain

AD/BD = AC/BC

AD/BD = AC/CP    (BC = CP by construction)

By using the converse of B.P.T (Basic Proportionality Theorem),

CD||BP

∠ACD = ∠CPB (Corresponding angles) … (3)

And, ∠BCD = ∠CBP (Alternate interior angles) … (4)

By construction, we have BC = CP.

∴ ∠CBP = ∠CPB (Angle opposite to equal sides of a triangle) … (5)

From equations (3), (4), and (5), we obtain

∠ACD = ∠BCD … (6)

In ΔCAD and ΔCBD,

∠ACD = ∠BCD (Using equation (6))

∠CDA = ∠CDB (Both 90°)

Therefore, the remaining angles should be equal.

∴∠CAD = ∠CBD

⇒ ∠A = ∠B

Question 7: If cot θ = 7/8, evaluate

(i) ((1 + sinθ) * (1 – sinθ))/(1 + cosθ) * (1 – cosθ)))

(ii) cot²θ

Solution:

(i) Using (a + b) * (a – b) = a² – b² in numerator and denominator

We get

(1 – sin²θ)/(1 – cos²θ)

Using sin²θ + cos²θ = 1

We get

cos²θ/sin²θ = cot²θ

Now

cot²θ = (7/8)2 = 49/64

(ii) cot²θ = (7/8)2 = 49/64

Question 8. If 3 cot A = 4, Check whether (1 – tan²A)/(1 + tan²A) = cos²A – sin²A

Solution.

We know that, tanA = sinA / cosA   ….(1)

Using (1) on L.H.S

= (1 – sin²A/cos²A)/(1 + sin²A/cos²A)

which on rearranging becomes

= (cos²A – sin²A)/(cos²A + sin²A)

Using the identity,

cos²A + sin²A = 1

LHS becomes

= (cos²A – sin²A)

This is equal to RHS.

LHS = RHS (for every value of cot A)

Hence, Proved.

Question 9: In ΔABC, right-angled at B. If tan A = 1/(3^1/2), find the value of

(i) sin A cos C + cos A sin C

(ii) cos A cos C − sin A sin C

Solution:

Using Pythagoras theorem

(AB)² + (BC)² = (AC)²

(31/2)² + (1)² = (AC)²

which gives

AC = 2 cm

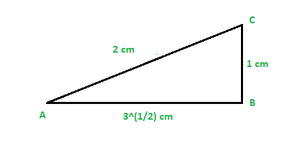
Using formulas

sin A = 1/2

sin C = 3^1/2/2

cos A = 3^1/2/2

cos C = 1/2

Now, (i) sin A cos C + cos A sin C

Substituting the values

= (1/2) * (1/2) + (3^1/2/2) * (3^1/2/2)

= 1/4 + 3/4

= 1

Now, (ii) cos A cos C − sin A sin C

Substituting the values

= (3^1/2/2) * (1/2) – (1/2) * (3^1/2/2)

= 3^1/2/4 – 3^1/2/4

= 0

Question 10: In ΔPQR, right-angled at Q, PR + QR = 25 cm and PQ = 5 cm. Determine the values of sin P, cos P, and tan P.

Solution:

Given that, PR + QR = 25

PQ = 5

Let PR be x cm.

Therefore, QR = 25 − x cm

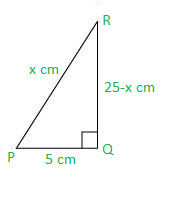
Applying Pythagoras theorem in ΔPQR, we obtain

PR² = PQ² + QR²

x² = (5)² + (25 − x)²

x² = 25 + 625 + x² − 50x

50x = 650

x = 13

Therefore, PR = 13 cm

QR = (25 − 13) cm = 12 cm

Now,

sin P = QR/PR = 12/13

cos P = PQ/PR = 5/13

tan P = QR/PQ = 12/5

Question 11. State whether the following are true or false. Justify your answer.

(i) The value of tan P is always less than 1.

(ii) sec A = 12/5 for some value of angle A.

(iii) cos A is the abbreviation used for the cosecant of angle A.

(iv) cot A is the product of cot and A

(v) sin θ = 4/3, for some angle θ

Solution:

(i) Consider a ΔPQR, right-angled at Q as shown below.

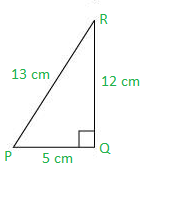
Here tan P = 12/5 which is surely greater than 1.

Therefore, the statement is false.

(ii) Consider ΔABC with AB = 5 cm, AC = 12 cm and BC = x cm

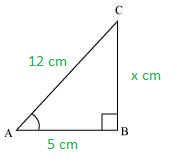
Using Pythagoras theorem in ΔABC

(AB)² + (BC)2 = (AC)2

52 + x2 = 122

x = (144 – 25)1/2

x = (119)1/2

x = 10.9 cm

AB < BC < AC

So this triangle is valid,

Therefore, given statement is true.

(iii) Abbreviation used for cosecant A is cosec A. And cos A is the abbreviation used for cosine A.

Hence, the given statement is false.

(iv) cot A is not the product of cot and A. It is the cotangent of ∠A.

Hence, the given statement is false.

(v) sin θ = 4/3 

In a right-angled triangle, hypotenuse is always greater than the remaining two sides. Therefore, such value of sin θ is not possible.

Hence, the given statement is false

NCERT Solutions for Class 10 Maths Chapter 8 Introduction to Trigonometry: Exercise 8.2

Question 1. Evaluate the following : 

(i) sin 60° cos 30° + sin 30° cos 60° 

Solution:

Formulas to be used : sin 30° = 1/2

                                      cos 30° = √3/2

                                      sin 60° = 3/2

                                      cos 60° = 1/2

=> (√3/2) * (√3/2) + (1/2) * (1/2)

=> 3/4 +1/4

=> 4 /4 

=> 1

(ii) 2 tan²45° + cos²30° – sin²60°

Solution:

Formulas to be used : sin 60° = √3/2

                                     cos 30° = √3/2

                                     tan 45° = 1

 => 2(1)(1) + (√3/2)(√3/2)-(√3/2)(√3/2)

 => 2 + 3/4 – 3/4

 => 2

(iii) cos 45°/(sec 30°+cosec 30°)

Solution: 

Formulas to be used : cos 45° = 1/√2

                                      sec 30° = 2/√3

                                      cosec 30° = 2

=> 1/√2 / (2/√3 + 2)

=> 1/√2 / (2+2√3)/√3   

=> √3/√2×(2+2 √3) = √3/(2√2+2√6)

=> √3(2√6-2√2)/(2√6+2√2)(2√6-2√2)

=> 2√3(√6-√2) / (2√6)²-(2√2)²

=> 2√3(√6-√2)/(24-8) = 2 √3(√6-√2)/16 

=> √3(√6-√2)/8

=> (√18-√6)/8  

=> (3√2-√6)/8

(iv) (sin 30° + tan 45º – cosec 60°)/(sec 30° + cos 60° + cot 45°)

Solution: 

Formulas to be used : sin 30° = 1/2

                                     tan 45° = 1

                                     cosec 60° = 2/√3

                                     sec 30° = 2/√3

                                     cos 60° = 1/2

                                     cot 45° = 1

=> (1/2+1-2/√3) / (2/√3+1/2+1)

=> (3/2-2/√3)/(3/2+2/√3)

=> (3√3-4/2 √3)/(3√3+4/2 √3)

=> (3√3-4)(3√3-4)/(3√3+4)(3√3-4)

=> (27+16-24√3) / (27-16)

=> (43-24√3)/11

(v) (5cos²60° + 4sec² 30° – tan²45°)/(sin²30° + cos²30°)

Solution:

Formulas to be used : cos 60° = 1/2

                                      sec 30° = 2/√3

                                      tan 45° = 1

                                      sin 30° = 1/2

                                      cos 30° = √3/2

=> 5(1/2)²+4(2/√3)²-1²/(1/2)+(√3/2)

=> (5/4+16/3-1) / (1/4+3/4)

=> (15+64-12) / 12/(4/4)

=> 67/12

Question 2. Choose the correct option and justify your choice:

(i) 2tan 30°/1+tan²30° =

(A) sin 60°            (B) cos 60°          (C) tan 60°            (D) sin 30°

(ii) 1-tan²45°/1+tan²45° =

(A) tan 90°            (B) 1                    (C) sin 45°            (D) 0

(iii)  sin 2A = 2 sin A is true when A =

(A) 0°                   (B) 30°                  (C) 45°                 (D) 60°

(iv) 2tan30°/1-tan²30° =

(A) cos 60°          (B) sin 60°             (C) tan 60°           (D) sin 30°

Solution: 

(i) In the given equation, substituting the value of tan 30° 

As tan 30° = 1/√3

2tan 30°/1+tan²30° = 2(1/√3)/1+(1/√3)²

=> (2/√3)/(1+1/3) = (2/√3)/(4/3)

=> 6/4√3 = √3/2 

=> sin 60°   

The ans is sin 60°. 

The correct option is (A).

(ii) In the given equation, substituting the of tan 45° 

 As tan 45° = 1

1-tan²45°/1+tan²45° = (1-1²)/(1+1²)

= 0/2 => 0

The ans is 0. 

The correct option is (D).

(iii) sin 2A = 2 sin A is true when A = 0°

sin 2A = sin 0° = 0

 2 sin A = 2 sin 0° = 2 × 0 = 0

 Another way :

 sin 2A = 2sin A cos A

=> 2sin A cos A = 2 sin A

=> 2cos A = 2 => cos A = 1

Now, we have to check which degree value has to be applied, to get the solution as 1.

When 0 degree is applied to cos value we get 1, i.e., cos 0 = 1

Hence, A = 0°

The correct option is (A).

(iv) As tan 30° = 1/√3

2tan30°/1-tan²30° =  2(1/√3)/1-(1/√3)²

=> (2/√3)/(1-1/3) = (2/√3)/(2/3) = √3 = tan 60°

The correct option is (C).

Question 3. If tan (A + B) = √3 and tan (A – B) = 1/√3, 0° < A + B ≤ 90°; A > B, find A and B.

Solution: 

tan (A + B) = √3 

tan (A + B) = tan 60°

(A + B) = 60° … (i)

tan (A – B) = 1/√3

tan (A – B) = tan 30°

(A – B) = 30° …  (ii)

Now add the equation (i) and (ii), we get

A + B + A – B = 60° + 30°

A= 45°

Substituting the value of A in equation (i) to find the value of B

45° + B = 60°

B = 60° – 45°   

 B = 15°

Hence, A = 45° and B = 15°

Question 4. State whether the following are true or false. Justify your answer.

(i) sin (A + B) = sin A + sin B.

(ii) The value of sin θ increases as θ increases.

(iii) The value of cos θ increases as θ increases.

(iv) sin θ = cos θ for all values of θ.

(v) cot A is not defined for A = 0°.

Solution: 

(i) Let us take A = 60° and B = 30°, then

Substitute the values of A and B in the sin (A + B) formula, we get

sin (A + B) = sin (60° + 30°) = sin 90° = 1 and,

sin A + sin B = sin 60° + sin 30°

= √3/2 + 1/2 = (√3 + 1 ) / 2, sin(A + B) ≠ sin A + sin B 

Since both the values obtained are not equal. 

Hence, the statement is false.

(ii) From the values given below, we can see that as angle(theta) increases value also increases.

sin 0° = 0, sin 30° = 1/2, sin 45° = 1/√2, sin 60° = √3/2 , sin 90° = 1

Thus, the value of sin θ increases as θ increases.

Hence, the statement is true. 

(iii) From the values given below, we can see that as angle (theta) increases value decreases.

cos 0° = 1, cos 30° = √3/2 , cos 45° = 1/√2, cos 60° = 1/2, cos 90° = 0

Thus, the value of cos θ decreases as θ increases. 

Hence, the statement given above is false.

(iv) sin θ = cos θ, is only true for theta = 45° 

Therefore, the above statement is false.

(v) As tan 0° = 0

cot 0° = 1 / tan 0° 

= 1 / 0 => undefined

Hence, the given statement is true.

NCERT Solutions for Class 10 Maths Chapter 8 Introduction to Trigonometry: Exercise 8.3

Question 1. Evaluate:

(i) sin 18° / cos 72°

Solution:

Since, 

cos 72°  = cos ( 90° – 18° ) = sin 18°

Therefore, 

sin 18° / cos 72° = sin 18° / sin 18°  = 1

Hence, sin 18° / cos 72°  = 1.

(ii) tan 26° / cot 64°

Solution:

Since,

cot 64°  = cot ( 90° – 26° ) = tan 26°

Therefore,

tan 26° / cot 64° = tan 26° /  tan 26°  = 1

Hence, tan 26° / cot 64°  = 1.

(iii) cos 48° – sin 42°

Since,

cos 48°  = cos ( 90° – 42° ) = sin 42°

Therefore,

cos 48° – sin 42° = sin 42° –  sin 42°  = 0

Hence, cos 48° – sin 42°  = 0.

(iv) cosec 31° – sec 59°

Solution:

Since,

sec 59°  = sec ( 90° – 31° ) = cosec 31°

Therefore ,

cosec 31° – sec 59° = cosec 31° – cosec 31°  = 0

Hence, cosec 31° – sec 59°  = 0.

Question 2. Show that:

(i) tan 48° tan 23° tan 42° tan 67° = 1

Solution:

Let A = tan 48° tan 23° tan 42° tan 67°

Since ,

tan 23° = tan( 90° – 23° ) = cot 67° and,

tan  42° = cot(  90° –  42° ) = cot  48°

Therefore,

A = tan 48° cot 67° cot  48° tan  67°

A = 1  (Since, tan B° cot  B° = 1)

Hence, tan 48° tan 23° tan 42° tan 67° = 1

 (ii) cos 38° cos 52° – sin 38° sin 52° = 0

Let A = cos 38° cos 52° – sin 38° sin 52°

Since,

sin 52° = sin (90° – 38°) = cos 38° and,

cos  52° = cos(90° –  52°) = sin 38°

Therefore,

A = cos 38° sin 38° – sin 38° cos 38°

A = 0                                               

Hence, cos 38° cos 52° – sin 38° sin 52° = 0.

Question 3. If tan 2A = cot (A – 18°), where 2A is an acute angle, find the value of A.

Solution:

We have, 

tan 2A = cot ( A – 18° )  —(1)

Since,

tan (2A) = cot ( 90° – 2A )  — (2)

Putting (2) in (1),

cot ( 90° – 2A ) = cot ( A – 18° ) 

Therefore,

90° – 2A = A – 18°

3A = 108°

A = 36°

Hence, A = 36°.

Question 4. If tan A = cot B, prove that A + B = 90°. 

Solution:

We have,

tan A = cot B —(1)

Since,

tan (A) = cot (90° – A)  — (2)

Putting (2) in (1),

cot (90° – A) = cot (B)

Therefore,

90° – A = B

Hence, A + B = 90°.

Question 5. If sec 4A = cosec (A – 20°), where 4A is an acute angle, find the value of A.

Solution:

We have,

sec 4A = cosec ( A – 20° )  —(1)

Since,

sec 4A = cosec ( 90° – 4A )  — (2)

Putting (2) in (1),

cosec ( 90° – 4A ) = cosec ( A  – 20° )

Therefore,

90° – 4A = A – 20°

5A = 110°

A = 22°

Hence, A = 22°.

Question 6. If A, B, and C are interior angles of a triangle ABC, then show that  sin ((B + C) / 2) = cos (A / 2).

Solution:

Let T = sin ((B + C) / 2) — (1)

A, B and C are the interior angles of triangle ABC, therefore,

A + B + C = 180° 

Dividing by 2 on both sides

(B + C)/2  = 90° – (A / 2) —(2)

Putting (2) on (1)

T = sin (90° – (A / 2) 

   = cos (A / 2)

Hence, sin ((B + C)/2) = cos (A / 2).

Question 7. Express sin 67° + cos 75° in terms of trigonometric ratios of angles between 0° and 45°

Solution:

Let A = sin 67° + cos 75°

Since,

sin 67° = sin(90° – 23°) = cos (23°)

cos 75° = cos (90° – 15°) = sin (15°)

Therefore,

sin 67° + cos 75° = cos 23° + sin 15°

NCERT Solutions for Class 10 Maths Chapter 8 Introduction to Trigonometry: Exercise 8.4

Question 1. Express the trigonometric ratios sin A, sec A, and tan A in terms of cot A

Solution:

(i) sin A

We know that

cosec²A = 1 + cot²A

1/sin²A = 1 + cot²A

sin²A = 1/(1 + cot²A)

sin A = 1/(1+cot²A)^1/2

(ii) sec A

sec²A = 1 + tan²A

Sec²A = 1 + 1/cot²A

sec²A = (cot²A + 1) / cot²A

sec A = (cot²A + 1)^1/2 / cot A

(iii) tan A

tan A = 1 / cot A

tan A = cot ^-1 A

Question 2. Write all the other trigonometric ratios of ∠A in terms of sec A.

Solution:

(i) cos A

cos A = 1/sec A

(ii) sin A

We know that

sin²A = 1 – cos²A

Also , cos²A = 1 / sec²A

sin²A = 1 – 1 / sec²A

sin²A = (sec²A – 1) / sec²A

sin A = (sec²A – 1)^1/2 / sec A

(iii) tan A

We know that

tan²A + 1 = sec²A

tan A = (sec²A – 1)½

(iv) cosec A

We know

cosec A = 1/ sinA

cosec A = sec A / (sec²A – 1)½

(v) cot A

We know

cot A = cos A / sin A

cot A = (1/sec A) / ((sec²A – 1)^1/2 / sec A)

cot A = 1 / (sec²A – 1)^1/2

Question 3. Evaluate:  

(i) (sin² 63° + sin² 27°)/(cos² 17° + cos² 73°)

(ii) sin 25° cos 65° + cos 25° sin 65°

(i) ([sin(90-27)]² + sin² 27) / ([cos(90-73)]² + cos² 73)

We know that 

sin(90-x) = cos x
cos(90-x) = sin x

(cos²(27) + sin² 27) / (sin²(73) + cos² 73)

Using 

sin²A + cos²A = 1

1/1 = 1

(ii) [sin 25 * cos(90-25)] + [cos 25 * sin(90-25)]

Using

sin(90-x) = cos x
cos(90-x) = sin x

= [sin 25 * sin 25] + [cos 25 * cos 25]

= sin² 25 + cos² 25

= 1

Question 4. Choose the correct option. Justify your choice.

Solution:

(i) 9 sec² A – 9 tan² A  

(A) 1 (B) 9 (C) 8 (D) 0 

Using sec²A – tan²A = 1 

9 (sec²A – tan²A ) = 9(1) 

Ans (B)

(ii) (1 + tan θ + sec θ) (1 + cot θ – cosec θ)

(A) 0 (B) 1 (C) 2 (D) –1 

Simplifying all ratios

= (1 + sinθ/cosθ + 1/cosθ) (1 + cosθ/sinθ – 1/sinθ)

= ((cosθ + sinθ + 1)/ cosθ) ((sinθ + cosθ – 1 )/sinθ)

= ((cosθ + sinθ)² – 1) / (sinθ cosθ)

= (1 + 2*cosθ*sinθ – 1) / (sinθ cosθ)

= 2

Ans (C)

(iii) (sec A + tan A) * (1 – sin A) 

(A) sec A (B) sin A (C) cosec A (D) cos A

Simplifying sec A and tan A

= (1/cos A + sin A/cos A)*(1 – sin A)

= ((1 + sin A)/cos A)*(1 – sin A)

= (1 – sin²A)/cos A

= cos²A / cos A

= cos A

Ans (D)

(iv) (1 + tan²A) / (1 + cot²A)

(A) sec²A (B) –1 (C) cot²A (D) tan²A

Simplifying tan A and cot A

= (1 + (sin²A / cos²A)) / (1 + (cos²A / sin²A))

= ((cos²A + sin²A) / cos²A) / ((cos²A + sin²A) / sin²A)

= sin²A / cos²A

= tan²A

Ans (D)

Question 5. Prove the following identities, where the angles involved are acute angles for which the expressions are defined.

Solution:

(i) (cosec θ – cot θ)² = (1 – cosθ) / (1 + cosθ)

Solving LHS

Simplifying cosec θ and cot θ

= (1-cos θ)² / sin²θ

= (1-cos θ)² / (1-cos²θ)

Using a² – b² = (a+b)*(a-b)

= (1-cos θ)² / [(1-cos θ)*(1+cos θ)]

= (1-cos θ) / (1+cos θ) = RHS

Hence Proved

(ii) (cos A / (1+sin A) + ((1+sin A) / cos A) = 2 sec A

Solving LHS

Taking LCM 

= (cos²A + (1+sin A)²) / ((1+sin A) cos A)

= (cos²A + 1 + sin²A + 2 sin A ) / ((1 + sin A)*cos A)

Using sin²A + cos²A = 1

= (2 + 2*sin A) / ((1+sin A)*cos A)

= (2*(1 + sin A)) / ((1 + sin A)*cos A)

= 2 / cos A

= 2 sec A = RHS

Hence Proved

(iii) (tan θ / (1 – cot θ)) + (cot θ / (1 – tan θ)) = 1 + sec θ*cosec θ

Solving LHS

Changing tan θ and cot θ in terms of sin θ and cos θ and simplifying

= ((sin²θ) / (cos θ *(sin θ-cos θ))) + ((cos²θ ) / (sin θ *(sin θ-cos θ)))

= (1 / (sin θ-cos θ)) * [(sin³θ – cos³θ) / (sin θ * cos θ)]

= (1 / (sin θ – cos θ)) * [ ((sin θ – cos θ) * ( sin²θ + cos²θ + sin θ * cos θ ))/(sin θ *cos θ)]

= (1+sin θ*cos θ) / (sin θ*cos θ)

= sec θ*cosec θ + 1 = RHS

Hence Proved

(iv) (1 + sec A) / sec A = sin²A / (1 – cos A)

Solving LHS

= cos A + 1

Solving RHS

= (1 – cos²A) / (1 – cos A)

= (1 – cos A) * (1 + cos A) / (1 – cos A)

= 1 + cos A = RHS

Hence Proved

(v) (cos A – sin A + 1) / (cos A + sin A – 1) = cosec A + cot A using the identity cosec²A = 1 + cot²A

Solving LHS

Multiplying numerator and denominator by (cot A – 1 + cosec A)

= (cot²A + 1 + cosec²A – 2*cot A – 2*cosec A + 2*cot A*cosec A) / (cot²A – (1 + cosec²A – 2*cosec A))

= (2*cosec²A – 2*cot A – 2*cosec A + 2*cot A*cosec A) / (cot²A – 1 – cosec²A + 2*cosec A) 

= (2* cosec A *(cosec A + cot A) – 2*(cosec A + cot A)) / (cot²A – 1 – cosec²A + 2*cosec A)

= ((cosec A + cot A) * (2*cosec A – 2 )) / (2*cosec A – 2) 

= cosec A + cot A = RHS

Hence Proved

(vi) [(1 + sin A) / (1 – sin A)]^½ = sec A + tan A

Solving LHS

Multiplying numerator and denominator by (1+sinA)

= [((1 + sin A)*(1 + sin A)) / ((1 – sin A)*(1 + sin A))]^½

= (1 + sin A) / (1 – sin²A)^½

= (1 + sin A) / (cos²A)^1/2

= (1 + sin A) / (cos A)

= sec A + tan A = RHS

Hence Proved

(vii) (sin θ – 2 sin³θ) / (2 cos³θ – cos θ) = tan θ

Solving LHS

= (sin θ * (1 – 2*sin²θ)) / (cos θ * (2*cos²θ – 1))

= (sin θ * (1 – 2*sin²θ )) / (cos θ * (2*(1 – sin²θ) – 1))

= (sin θ *(1 – 2*sin²θ)) / (cos θ * (1 – 2*sin²θ))

= tan θ = RHS

Hence Proved 

(viii) (sin A + cosec A)² + (cos A + sec A)² = 7 + tan²A + cot²A

Solving LHS

= sin²A + cosec²A + 2*sin A *cosec A + cos²A + sec²A + 2*cos A *sec A

We know that cosec A = 1 / sin A

= 1 + 1 + cot²A + 1 + tan²A + 2 + 2

= 7 + tan²A + cot²A = RHS

Hence Proved

(ix) (cosec A – sin A)*(sec A – cos A) = 1 / (tan A + cot A)

Solving LHS

= ((1/sin A) – sin A) * ((1/cos A) – cos A)

= ((1 – sin²A) / sin A) * ((1 – cos²A) / cos A)

= (cos²A * sin²A) / (sin A * cos A)

= sin A * cos A

Solving RHS

Simplifying tan A and cot A

= (sin A * cos A) / ( sin²A + cos²A)

= sin A * cos A = RHS

Hence Proved

(x) (1 + tan²A) / (1 + cot²A ) = [(1 – tan A) / (1 – cot A)]² = tan²A

Solving LHS

Changing cot A = 1 / tan A

= (tan²A * (1 + tan²A)) / (1 + tan²A) = tan²A = RHS

= [(1 – tan A) / (1 – cot A)]² = (1 + tan²A – 2*tan A) / (1 + cot²A – 2*cot A)

= (sec²A – 2*tan A) / (cosec²A – 2*cot A)

Solving this we get 

= tan²A

Hence Proved

Key Features of NCERT Solutions for Class 10 Maths Chapter 8 Introduction to Trigonometry:

• NCERT Solutions are created for each chapter including Class 10 Maths Chapter 8 Introduction to Trigonometry.
• These solutions provide in-depth solutions to the problems encountered by students in their NCERT Class 10 Maths textbook.
• These solutions are very accurate and comprehensive, which can help students of Class 10 prepare for any academic as well as competitive exams.

NCERT Solutions for Class 10 Maths Chapter 8 Introduction to Trigonometry- FAQs

Q1: Why is it important to learn Class 10 Maths Chapter 8 Introduction to Trigonometry?

Trigonometry is used to set directions. It also tells you the direction to point the compass in order to travel straight forward. To find a certain location, it is used in navigation. It is also used to calculate the separation between a location in the water and the coast.

Q2: What topics are covered in NCERT Solutions for Class 10 Maths Chapter 8 Introduction to Trigonometry?

NCERT Solutions for Class 10 Maths Chapter 8 Introduction to Trigonometry covers topics such as trigonometric ratios and their calculation with the help of Pythagoras theorem, calculation of specific angles like 0 degrees, 30 degrees, 45 degrees, and 90 degrees and the use of the trigonometric table, complementary angle, and trigonometric identities. 

Q3: How can NCERT Solutions for Class 10 Maths Chapter 8 Introduction to Trigonometry help me?

NCERT Solutions for Class 10 Maths Chapter 8 Introduction to Trigonometry can help you solve the NCERT exercise without any limitations. If you are stuck on a problem you can find its solution in these solutions and free yourself from the frustration of being stuck on some question.

Q4: How many exercises are there in NCERT Class 10 Maths Chapter 8 Introduction to Trigonometry?

There are 4 exercises in the Class 10 NCERT Maths Chapter 8 Introduction to Trigonometry which covers all the important topics and sub-topics.

Q5: Where can I find NCERT Solutions for Class 10 Maths Chapter 8 Introduction to Trigonometry?

You can find NCERT Solutions for Class 10 Maths Chapter 8 Introduction to Trigonometry in this article, created by our team of experts at GeeksforGeeks.