Chance is defined as the natural occurrence of any event without any interference, we can also say that the possibility of any event is the chance of the event, and mathematically we define the chance as the probability of an event.
Probability refers to the likelihood of the occurrence of an event. The event may or may not occur. For example, we have some of the real-life statements which we hear in our daily lives:
- My uncle may visit us today
- There is a good chance that it may rain tomorrow
- The school may probably take us to a picnic in June
- Schools may reopen in March
These daily life statements use terms like ‘probable’, ‘may’, ‘has a good chance’, ‘likely’ etc., so it is clear that there is no surety of occurrence, it may occur, or it may not occur, so this is called chance. In other words, a chance is a possibility of something happening. And in mathematics, probability is known as chance. Chance and Probability is an important topic for Class 7 and Class 8 students.

In this article, we will learn about, Chance, Probability, Formula of Probability, and others in detail. The concepts of probability are frequently used in Statistics, engineering, data science, and hypothesis testing.
Interpretation of Probability
We simply define the probability of an event as the chance of occurring that event and mathematically it is defined as the ratio of the desired outcome to the total outcome related to any event. We can understand the same by using the formula,
P(E) = Number of Outcomes in which event E occurred/Total Number of Possible Outcomes
Suppose we have to find the probability of drawing a black queen in a well-shuffled deck of cards. Then we know that there are 52 cards in a deck and the probability of each card is the same and there are only two black queens in the deck, then the required probability of the event say P(E) is
P(E) = 2/52 = 1/26
We can change the same into a percentage as, by multiplying 1/26 with 100 and the result is,
1/26 × 100 = 4% (approx)
Probability Formula
- This formula is used to calculate the probability of an event to occur. Suppose an event E is happening and the Probability of happening the event E is P(E) then,
P(E) = (Favourable Outcomes)/(Total Outcomes)
Note: The value of probability ranges from 0 to 1.
- Suppose the probability of happening an event is P(E) and the probability of non-occurring that event is, P(
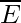 ). The formula used to calculate the probability of a non-occurrence of an event is,
). The formula used to calculate the probability of a non-occurrence of an event is,
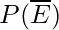 = 1 – P(E)
= 1 – P(E)
Here,  is a probability of a non-occurring event E. It is also known as the complement of an event E.
is a probability of a non-occurring event E. It is also known as the complement of an event E.
Chance and Probability of Events
In any experiment or general event all the possible cases that can happen are called the sample space of the event or it is also called the total possible outcome of the event. In any case, there are some outcomes that we favor and these outcomes are called favorable outcomes and probability of any event is calculated by the formula as,
Probability of any Event”E” {P(E)} = (Favourale Outcomes)/(Total Outcomes)
Suppose in an experiment we are given with first 10 natural numbers as, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 and we have to choose a number from those 10 numbers random then the probability that is an even number greater than 5 is,
Total Outcomes of the Experiment = 1, 2, 3, 4, 5, 6, 7, 8, 9, 10
Favorable Outcomes of the Experiment = 6, 8, and 10
Probability = (Total Outomces)/ (Favourable Outcomes)
= 3/10
= 3/10 × 100 = 30%
Then we can say that there is a 30% chance that the outcome is an even number greater than 5.
Terminology Related to Chance and Probability
Some fundamental concepts associated with probability are explained below, students are advised to read all the points in detail to get a complete idea about probability.
- Experiment: A trial in which some well-defined outcome is expected is called an experiment.
- Outcome: The result of an experiment is called outcome. For example, head/tail are possible outcomes while tossing a coin.
- Sample Space: A set of all possible outcomes is called sample space. For example, while tossing a coin, sample space S is
S = {H, T}, where H refers to the Head and T refers to the Tails
- Random Experiment: A random experiment is an experiment whose outcome may not be predicted in advance. It may be repeated under numerous conditions. Some examples of random experiments are,
- Tossing a Coin – Head and tails are the possible outcomes.
- Rolling a Dice – There are six possible outcomes, 1, 2, 3, 4, 5, and 6.
- Equally Likely Outcomes: The equally Likely Outcomes refers to a condition when each outcome of an experiment is equally likely. In other words, each outcome has the same chance of occurring. For example, while tossing a fair coin, there are equal chances to get a head or a tail.
- Likely chances to probability: Let us consider the following cases to understand likely chances to probability.
Case 1: Tossing a coin
While tossing a coin, the sample space = {H, T}. There are two possible outcomes Head and tail, since both outcomes are equally likely, we can conclude that the likelihood of getting head = 1/2. Similarly, the likelihood of getting a tail = 1/2
Case 2: Rolling a Dice
Sample space = {1, 2, 3, 4, 5, 6}
Total possible outcomes = 6
Since all outcomes have an equal chance, so the likelihood of occurrence of each outcome = 1/6
- Outcomes of Events: The occurrence of each outcome in an experiment forms an event. For example, in the experiment of tossing a coin, the occurrence of the head, as well as the occurrence of a tail, are considered events.
- Impossible Events: When the probability of an event is 0, then the event is known as an impossible event. An example of an impossible event is, “The Sun Rises in the West.”
- Sure Events: When the probability of an event is 1, then the event is known as a sure event. An example of the sure event is, “The Sun Rises in the East.”
Applications of Probability in Real Life
Various application of the probability that we observed in our real life is,
- Weather Prediction: Metrological department observes the trends from data over many years to predict the weather.
- Exit Polls: Exit polls are carried out to get an idea of the chances of winning candidates.
- Strategic Planning: Businessmen study sales trends in a period of time to predict future sales. This helps them to plan strategically to provide them with more profits.
Read More,
Examples on Probability
Example 1: Find the probability of getting an odd number while rolling a die.
Solution:
Sample Space = {1, 2, 3, 4, 5, 6}
Total Outcomes = 6
Favourable Outcome {Odd Numbers} = {1, 3, 5}
Probability = (Favourable Outcome)/ (Total Outcome)
P(E) = 3/6 = 1/2
Example 2: A spinning wheel has 7 green sectors, 5 red sectors, and 4 blue sectors. Find the probability of getting a red sector. Also, find the probability of getting non-red sectors.
Solution:
Number of Green Sectors = 7
Number of Red Sectors = 5
Number of Blue Sectors = 4
Total Number of Sectors = 7 + 5 + 4 = 16
Probability of getting a Red Sector = No. of Red Sectors / Total Number of Sectors
P(E) = 5/16
Probability of getting a Non-Red Sector = 1 – Probability of getting a Red Sector
P(E)’ = 1 – 5/16
P(E)’ = 11/16
Example 3: Find the probability of getting a multiple of 3 when a die is rolled.
Solution:
While rolling a die possible outcomes = {1, 2, 3, 4, 5, 6}
Total number of possible outcomes = 6
Multiples of 3 = {3, 6}
Number of desired outcomes = 2
Probability of getting a multiple of 3 = Number of Desired Outcomes / Total Number of Possible Outcomes
P(E) = 2/6
P(E) = 1/3
Example 4: Find the probability of getting a card of kings from a deck of 52 cards.
Solution:
Total number of cards = 52
Number of king cards = 4
Probability = Number of Desired Outcomes / Total Number of Possible Outcomes
P(E) = 4/52
P(E) = 1/13
Example 5: Find the probability of picking vowels in the word ‘CHAMPION’
Solution:
Total number of letters in the word ‘CHAMPION’ = 8
Vowels in the word CHAMPION = A, I, O
Number of desired outcomes = 3
Probability = Number of Desired Outcomes / Total Number of Possible Outcomes
P(E) = 3/8
Example 6: A bag is filled with balls. Some of these balls are red in color. The probability of picking a red ball is x/2. Find “x” if the probability of picking a non-red ball is 2/3.
Solution:
P(Red Ball) + P(Non-Red Ball) = 1
Given,
- P(red ball) = x/2
- P(non-red ball) = 2/3
=> x/2 + 2/3 = 1
=> x/2 = 1 – 2/3
x/2 = 1/3
x = 2/3
Example 7: There are 24 students in a class. Out of these, 24 students, 16 are boys and the remaining are girls. Find the probability of selecting a girl randomly.
Solution:
Given,
- Total Number of Students = 24
- Boys = 16
- Girls = 24 – 16 = 8
P(selecting a girl) = Number of Girls/Total Number of Students
P(E) = 8/24 = 1/3
Example 8: There are 20 defective bulbs in a box of 500 electric bubs. Find the probability of randomly selecting a non-defective bulb.
Solution:
Given,
- Total Number of Bulbs = 500
- Defective Bulbs = 20
- Number of Non-Defective Bulbs = 500 – 20 = 480
P(selecting a non-defective bulb) = Number of Non-Defective Bulbs/Total Number of Bulbs
P(E) = 480/500
P(E) = 24/25
FAQs on Chance and Probability
What is meant by Chance?
The possibility of occurring an event is called the chance of an event. Suppose Messi takes 1 out of 3 penalty corners from its past record, then the chance of hitting a penalty corner by Messi is, 1/3 or 33%.
What is Probability in Mathematics?
In mathematics, chances are called probability and we define probability as the ratio of, favorable outcomes to the total outcomes of any event.
What is Probability Formula?
The probability formula or the formula used to find the probability of any event is,
P(E) = Favourable Event (Numbers)/Total Event(Numbers)
Where is Probability used in Real-Life?
The probability formula in real life is used to find the outcome of various events.
- It is used in weather forecasting
- It is used in Stocks Prediction
- It is used in defining the behavior pattern of consumers.
- It is used in predicting the growth of a company, etc.
Share your thoughts in the comments
Please Login to comment...