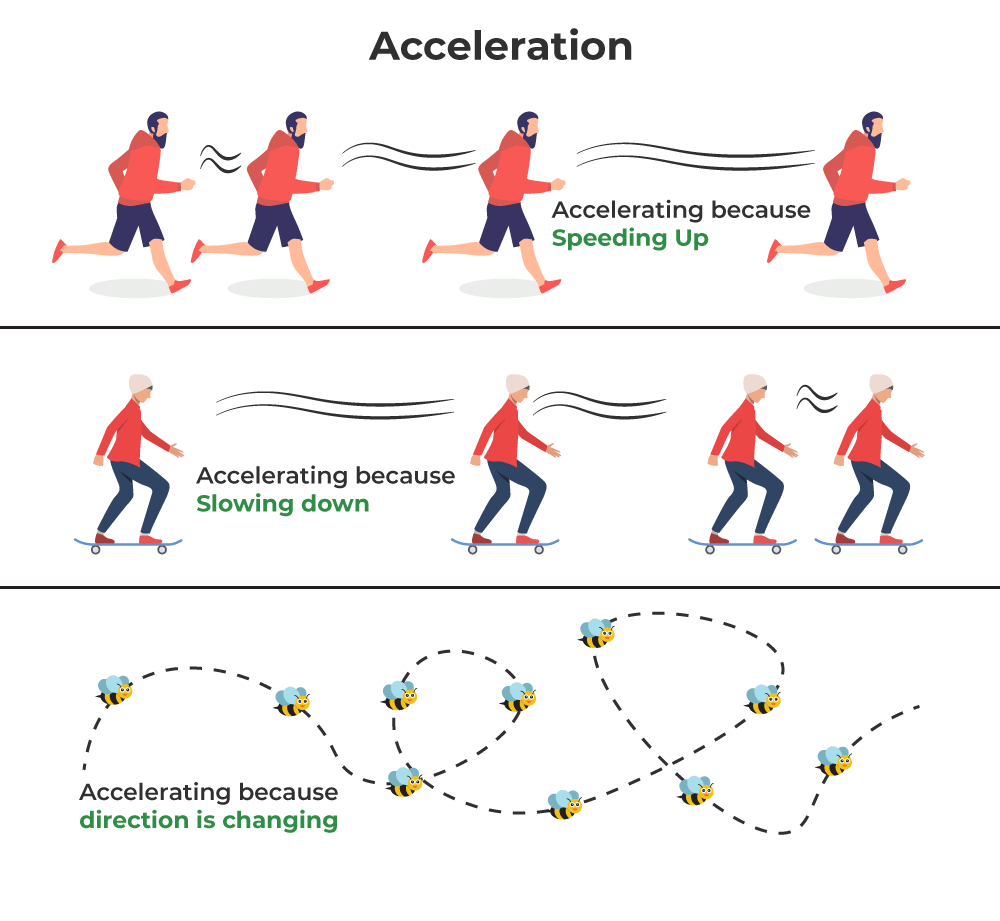
Acceleration

Acceleration is defined as the rate of change in velocity. This implies that if an object’s velocity is increasing or decreasing, then the object is accelerating. Acceleration has both magnitude and direction, therefore it is a Vector quantity. According to Newton’s Second Law of Motion, acceleration is defined as the ratio of the force applied to the object to the mass of the object. 

Let’s understand more about acceleration and related concepts like Acceleration Formula, its Unit, Types, Graphs, Solved Examples, and FAQs on it, in this article!

What is Acceleration?

Acceleration is defined as the rate of change of the velocity of an object with respect to time. An object is said to be accelerating or have the acceleration when its velocity is changing.

Acceleration can also be termed as the rate of change in velocity and the change over time. An acceleration vector’s magnitude tells us how much the velocity will change, while its direction tells us how the velocity will change i.e. whether the velocity is increasing or decreasing, the velocity vector is changing direction, or some combination of the three.

Acceleration can be positive, zero, or negative. In case the object’s velocity increases with time, it can be termed Positive Acceleration. In case the velocity is zero, it is termed Zero Acceleration, while the negative acceleration also known as retardation indicates a decrease in velocity with time.

Acceleration Formula

Mathematically, the change in the velocity of an object in motion is defined as, (v – u) where v and u are the final and the initial velocities.

Therefore, the acceleration of the object is given by,

Acceleration = Change in Velocity / Time Taken

a = (v – u) / t

where 
a is the acceleration, 
v is the final velocity,
u is the initial velocity, and
t is the time taken by the object

Unit of Acceleration 

• It is a vector quantity, which is associated with both magnitude and direction. It is denoted by ‘a’. 
• The unit of acceleration is meters per second squared or meters per second (the object’s speed or velocity) per second or m/s².

Note: Dimensional Formula of Acceleration is [M⁰ L¹ T^-2]

Types of Acceleration 

Following are the different types of acceleration associated with an object,

• Uniform Acceleration 
• Non-Uniform Acceleration 
• Average Acceleration
• Instantaneous Acceleration

Now let’s learn about each type of acceleration in detail.

Uniform Acceleration 

In case the velocity of an object changes in equal amounts during the same time interval, then the body is said to be in uniform acceleration.  In this case, neither the direction nor magnitude changes with respect to time.

For Examples:

• A ball rolling down the slope.
• When a bicycle rider is riding the bicycle on a slope where both pedals are engaged.
• A kid sliding down from the slider.
• Motion of car with constant velocity, etc

Non-Uniform Acceleration 

Variable acceleration is the velocity of the body that changes by varying amounts during the same time interval. Variable acceleration comes into the picture when the object’s direction or magnitude or both changes with respect to time.

For Examples:

• A car changing speed
• Uniform circular motion
• The motion of the pendulum with changing speed

Average Acceleration

The average acceleration is defined as the change in velocity for a particular specified time interval. The average acceleration can be calculated for a time instance, as follows, 

a_v = Δ v / Δ t

or

a_v = (v_f – v_i) / (t_f – t_i)

where 

• v_f is the final velocity, 
• v_i is the initial velocity, 
• t_i is the initial time and 
• t_f is the final time.

Instantaneous Acceleration

In order to calculate the instantaneous acceleration, the average velocity can be computed between two points in time separated by Δt and let Δt approach zero. The result obtained is the derivative of the velocity function v(t), which is instantaneous acceleration. Mathematically,

Thus, similar to velocity being the derivative of the position function, instantaneous acceleration is the derivative of the velocity function. We can show this graphically in the same way as instantaneous velocity. In (Figure), instantaneous acceleration at time t₀ is the slope of the tangent line to the velocity-versus-time graph at time t₀. We see that average acceleration given as,  

Velocity-Time Graph

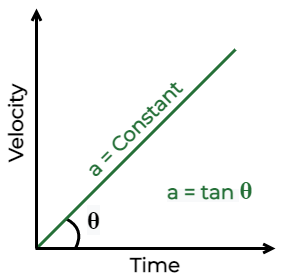
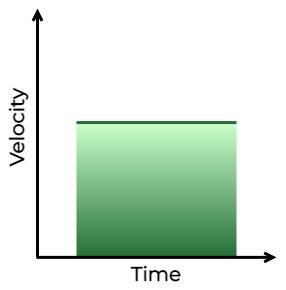
The curves indicate the velocity-time graph time is plotted along the x-axis and velocity is plotted along the y-axis. While finding displacement through the v – t graph, keep the sign under consideration.

• When the velocity of the particle is constant or acceleration is zero.

• When the particle is moving with a constant acceleration and its initial velocity is zero.

• When the particle is moving with constant retardation.

• When the particle moves with non-uniform acceleration and its initial velocity is zero.

• When the acceleration decreases and increases.

• The total area enclosed by the time-velocity curve represents the distance travelled by a body.

Difference Between Acceleration and Velocity

Here are some important differences between Acceleration and Velocity,

Acceleration	Velocity
Acceleration is defined as the time rate change of velocity.	However, velocity is the time rate of change of displacement.
Acceleration can be positive or negative, not zero.	While velocity can be zero, positive or negative.
The SI unit of Acceleration is m/s2.	The SI unit of velocity is m/s.
The formula for acceleration is, Acceleration = Velocity/Time	The formula for velocity is, Velocity = Acceleration/Time

Solved Examples on Acceleration

Example 1: If a truck accelerates from 6 m/s to 10 m/s in 10 s. Calculate its acceleration.

Solution:

Given that,

Initial Velocity, u = 6 m/s,

Final Velocity, v = 10 m/s,

Time taken, t = 10 s.

We have to find Acceleration ‘a’

Acceleration, a = (v – u) / t

                        = (10 m/s – 6  m/s) / 10 s

                        = 0.4 m/s²

Thus, the acceleration of the truck is 0.4 m/s².

Example 2: If a ball is released from the terrace of a building to the ground. If the ball took 6 s to touch the ground. Find the height of the terrace from the ground.

Solution:

Given that, 

Initial Velocity u = 0 {as the ball was at rest},

Time taken by the ball to touch the ground t = 6 seconds 

Acceleration due to gravity a = g = 9.8 m/s², 

Distance traveled by stone = Height of bridge  = s

The distance covered by the ball from the terrace to the ground

Therefore, 

Distance of the terrace from the ground is 29.4 m.

Example 3: If a man is driving the car at 108 km/h slow down and bring it to 72 km/h in 5 s. Calculate the retardation of the car?

Solution: 

Given that,

Initial velocity, u = 108 km/h or 

Final velocity, v = 72 km/h or 

Time taken, t = 5 seconds

Therefore, acceleration is,

The negative sign shows retardation.

Example 4: If a car moves from rest and then accelerates uniformly at the rate of 7.5 m/s² for 10 s. Find the velocity of the train in 10 s.

Solution:

Given that,

Initial velocity u = 0 {as the car was at rest}

Acceleration a = 7.5 m/s²

Time t = 10 s

v = u + at

   = 0 + 7.5 × 10

   = 75 m/s

Example 5: If an object moves along the x-axis according to the relation x = 1 – 2t + 3t², where x is in meters and t is in seconds. Calculate the acceleration of the body when t = 3s.

Solution:

Given that,

x = 1 – 2t + 3t²

Velocity, v = dx/dt  

                = d/dt {1 – 2t + 3t²}

                = -2 + 6t

Therefore, Acceleration a = dv/dt

                                        = d/dt {-2 + 6t}

                                        = 6 m/s² 

FAQs on Acceleration

Question 1: What is Radial Acceleration?

Answer:

The acceleration of an object along the radius towards the center of the radial path is called the radial acceleration.

Question 2: What is Acceleration due to Gravity?

Answer:

The acceleration due to gravity is defined as the acceleration experienced by the earth’s gravitational pull. It value is 9.8 m/s²

Question 3: What is Tangential Acceleration?

Answer:

Tangential acceleration is the rate at which a tangential velocity varies in the rotational motion of any object. It acts in the direction of a tangent at the point of motion for an object. 

Question 4: What do you understand by Centripetal Acceleration?

Answer:

Centripetal Acceleration is defined as the acceleration points towards the center of the curvature, now since the velocity is continuously changing and acceleration is present. 

Question 5: How to find the Acceleration?

Answer:

The formula to find the acceleration of any object is,

a = (v – u) / t

where,
v is final velocity,
u is initial velocity,
t is the time taken

Question 6: What is the SI unit of Acceleration?

Answer:

The SI unit of the accerelation is m/s²

Question 8: What is Uniform Acceleration?

Answer:

When an object accelerates uniformly i.e. its velocity increases linearly with time then it is called to be in uniform acceleration

Question 9: What is the Acceleration of any object in Free Fall?

Answer:

In free fall the acceleration of an object is also called the acceleration due to gravity and is equal to 9.8m/s²