Take something in your hand and toss it down. Its speed is zero when you free it from your grip. Its pace rises as it descends. It flies faster the longer it goes. This sounds like acceleration.
Acceleration, on the other hand, implies more than just rising speed. Pick up the same object and throw it into the air vertically. It will slow down on the way up until it comes to a halt and reverses course. Acceleration may also be described as a decrease in speed. However, acceleration is more than just a change of height.
Pick up your battered object and give it one last launch. This time, toss it horizontally and see how the horizontal velocity increases as the vertical velocity decrease. This change of direction is often called acceleration since acceleration is the rate of change in velocity with time and velocity is a vector quantity. The acceleration in both of these cases was caused by gravity. Since gravity was dragging the object down, it was speeding up. Even the straight-up object is dropping — and it starts falling the moment it leaves your side. If it hadn’t been, it would have proceeded in a straight line away from you. This is the acceleration due to gravity.
Now, Let’s discuss some basics before understanding the factors affecting acceleration due to gravity.
What is Gravity?
The universal force of attraction among all the entities or matter in this universe is also known as gravity. It can be considered as the driving force which pulls together all the matter. Gravity is measured in terms of the acceleration or movement that it gives to freely falling objects. At Earth’s surface, the value of the acceleration of gravity is about 9.8 m/s2. Thus, for every second an object is in free fall, its speed increases by about 9.8 m/s2.
Some important that one must learn before going on further are:
- There exist a direct correlation between mass and gravity, that is, mass is directly proportional to gravity. The heavier the object, the greater the intensity of pull. For instance, stars and sun, have greater gravity.
- Direct relation also exists between the mass of the object and gravity, that is increase in mass leads to increase in the pull due to gravity.
- Gravity is also inversely proportional to the distance between two objects.
Acceleration due to Gravity
The Earth pulls any particle lying on its surface towards its center with a force known as gravitational pull of gravity. When a force acts on a body, it causes acceleration, and in the case of gravitation, this acceleration caused by gravity is referred to as acceleration due to gravity
Acceleration due to gravity, usually referred by the symbol ‘g‘ is the acceleration attained by any object in the universe due to gravitational force.
The SI unit of acceleration due to gravity is m/s2.
The value of g in SI system is 9.806 ms-2. And the value of g in CGS system is 980 cm s-2.
The Dimensional Formula for g is [ M0 L1 T-2 ].
It has a magnitude as well as direction. Thus it is a vector quantity.
Derivation of the formula for Acceleration due to Gravity
Near the surface of Earth, the acceleration due to gravity is approximately constant. But, at large distances from the Earth, or around other planets or moons, it is varying. The acceleration due to gravity depends on the terms as the following:
- Mass of the body,
- Distance from the center of mass,
- Constant G i.e. Universal gravitational constant.
Let’s consider an object of mass m, on which the acceleration due to gravity g is acting, now suppose F is the force acting on it and is given by:
F = mg ……(1)
where F is the force acting on the object,
g is the acceleration due to gravity and
m is the mass of the object.
According to the universal law of gravitation, the attractive gravitational force is given as:
F = (G × m × M) / (r+h)2
where F is the force between two objects,
G is the universal gravitational constant (6.67 × 10-11 Nm2 / kg2),
M is the mass of the earth,
r is the radius of the earth, and
h is the height at which the body is from the surface of the earth.
Since the height is negligibly small compared to the radius of the earth, so the last equation can be rewritten as:
F = (G × m × M) / r2 ……(2)
Lets equate equation (1) and (2) and solve to evaluate the expression for g as:
mg = (G × m × M) / r2
g = GM / r2
Hence, the formula of acceleration due to gravity is evaluated as shown above.
Factors affecting Acceleration due to Gravity
g is majorly affected by the following four factors:
- The shape of the Earth.
- Rotational motion of the Earth.
- Altitude above the Earth’s surface.
- Depth below the Earth’s surface.
Variation of g due to shape of the Earth
The earth is not perfectly spherical, but is an oblate spheroid. The polar radius (radius near poles) of the earth is 21 km smaller than its equatorial radius (near the equator). As per the formula derived, the acceleration due to gravity is inversely proportional to the square of the radius of the earth
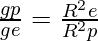
Where, ge and gp are the accelerations due to gravity assumed at the equator and poles, Re and Rp are the radii of earth near the equator and poles, respectively.
From the above equation, it can be easily derived that acceleration due to gravity is more at poles and less at the equator, that is ge < gp . Thus, acceleration due to gravity increases when one moves from the equator to the pole.

Rotational motion of the Earth.
Let us assume, ω is the angular velocity of rotation of earth about its own axis, then the acceleration due to gravity at a place having latitude λ is shown as
g′ = g – Rω² cos² λ
Here, λ at poles is 90° and λ at the equator is 0°.
g’ = g

Thus, there is no effect of rotation of earth about its own axis at poles.
At the equator,
λ = 0° and g’ = g – Rω²
The value of g is minimum at the equator.
If earth stops its rotation about its own axis, then g will remain unchanged at poles but increases by Rω² at the equator.
Hence, we can conclude that;
Acceleration due to gravity is minimum at the equator.
At poles, θ=90°
Acceleration due to gravity is maximum at poles.
Altitude above the Earth’s surface
Assume a mass ‘m’ that is under the effect of earth’s gravity at a height ‘h’ from earth’s surface. The force due to gravitational pull acting on the object is;

Acceleration due to gravity at the height ‘h’ from the Earth’s surface
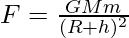 ……..(i)
……..(i)
Here,
M is the mass of earth
R is the radius of the earth.
The acceleration due to gravity at a certain height is given by ‘h’
Therefore,
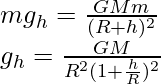 ……(ii)
……(ii)
Then, the acceleration due to gravity on the surface of the earth is shown by;
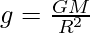 ………..(iii)
………..(iii)
After dividing equation (iii) and (ii) we will get,
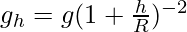 …………(iv)
…………(iv)
It is clear that the value of g decreases with an increase in height of an object. Hence, the value of g becomes zero at infinite distance from the earth.
Depth below the Earth’s surface.
The acceleration due to gravity on the surface of the earth is given by
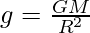
Assume 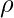 be the density of the material of the Earth
be the density of the material of the Earth
As we know
Mass = volume × density
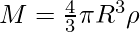 …….(i)
…….(i)
Thus, if we put the value of (i) in g, we will get

Also, let us assume the body to be taken to the depth ‘d’ below the surface of the earth. Then acceleration due to gravity gd at the depth ‘d’ below the Earth’s surface is shown as;
 ……..(iii)
……..(iii)
Now, divide the equation (iii) by (ii), we will get
Here, equation (iv) is an expression for the acceleration due to gravity at the depth ‘d’ below the surface of the earth.
From equation (iv) we get to know that acceleration due to gravity decreases as we go down into the Earth.
At the Centre of earth d = R,
Thus, acceleration due to gravity at the Centre of the earth is 0.
Sample Problems
Problem 1: At what height above the surface of the earth value of acceleration due to gravity is reduced to one by ninth of its value on the surface of the earth?
Solution:
From the formula
gh = 
Here gh = acceleration due to gravity at height ‘h’
g = acceleration due to gravity
R = radius of the earth
Thus,
From the problem
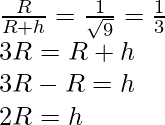
Hence,
At twice the height of the radius of the Earth value of acceleration due to gravity is reduced to one by ninth of its value on the surface of the earth.
Problem 2. If the radius of the Earth is decreased by 2% while keeping its mass the same, how will the acceleration due to gravity change?
Solution:
As we know that
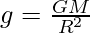
Where,
g = acceleration due to gravity
R = radius of the Earth
M = mass of the Earth
If R is decreased by 2% it will become 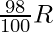
Therefore,
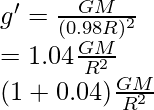
Therefore,
g’ increases by 0.04 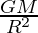 therefore increases by 4%.
therefore increases by 4%.
Problem 3. At what height from the surface of the earth will the value of ‘g’ be reduced by 19% of its value at the surface of the earth.
Solution:
g’ = 81% of g
g’ = 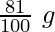
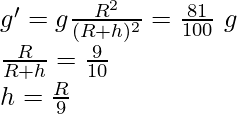
Therefore,
At the height of 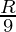 from the Earth surface the value of ‘g’ will be reduced to 19% of its value at the surface of earth.
from the Earth surface the value of ‘g’ will be reduced to 19% of its value at the surface of earth.
Problem 4. How many times is the acceleration due to gravity on the surface of Jupiter as compared to Earth’s surface?
(Use the following data: mEarth = 5.98 × 1024 kg, rEarth = 6.4 × 106 m, mJupiter = 1.9 × 1027 kg, rJupiter = 6.99 × 107 m)
Solution:
To solve this example we will need to find the ratio of acceleration due to gravity of Jupiter to acceleration due to gravity of Earth
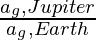
By the relation;
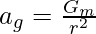
Here,
m = mass of planet
r = radius of planet

Thus, the acceleration due to gravity on Jupiter surface is 2.66 times more than that of Earth’s surface.
Problem 5. Explain acceleration due to gravity increase or decrease with the increase in the altitude?
Solution:
As we know that acceleration due to gravity at the depth of h is shown as;
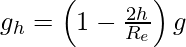
Here,
Re = Radius of the Earth
g = Acceleration due to gravity on the surface of the Earth
Thus, we can clearly see that from the equation that acceleration due to gravity increases with decrease in height and decreases with increase in height.
Problem 6. Explain that acceleration due to gravity is independent of the mass of earth as well as the mass of the body?
Solution:
As we know that acceleration due to gravity of body of mass m is shown as;
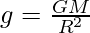
Here,
G = Is the universal gravitational constant
M = Mass of the Earth
R = Radius of the Earth
Thus, we can clearly see here that acceleration due to gravity is independent of the mass.
Problem 7. Explain that acceleration due to gravity is increased or decreases with the increase in depth?
Solution:
As we know that acceleration due to gravity is shown as;
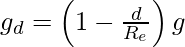
Thus, here we can clearly see that the acceleration due to gravity increases with decrease in depth and decreases with increase in depth.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...