Skip to content
Related Articles

Related Articles

0-1 BFS (Shortest Path in a Binary Weight Graph)

View Discussion
Improve Article
Save Article
Like Article

Given a graph where every edge has weight as either 0 or 1. A source vertex is also given in the graph. Find the shortest path from source vertex to every other vertex. 
Example: 
 

Input : Source Vertex = 0 and below graph 


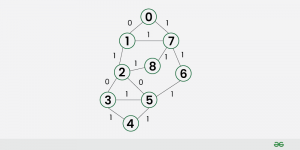
Output : Shortest distances from given source
         0 0 1 1 2 1 2 1 2

Explanation : 
Shortest distance from 0 to 0 is 0
Shortest distance from 0 to 1 is 0
Shortest distance from 0 to 2 is 1
..................

 

In normal BFS of a graph all edges have equal weight but in 0-1 BFS some edges may have 0 weight and some may have 1 weight. In this we will not use bool array to mark visited nodes but at each step we will check for the optimal distance condition. We use double ended queue to store the node. While performing BFS if a edge having weight = 0 is found node is pushed at front of double ended queue and if a edge having weight = 1 is found, it is pushed at back of double ended queue.
The approach is similar to Dijkstra that the if the shortest distance to node is relaxed by the previous node then only it will be pushed in the queue. 
The above idea works in all cases, when pop a vertex (like Dijkstra), it is the minimum weight vertex among remaining vertices. If there is a 0 weight vertex adjacent to it, then this adjacent has same distance. If there is a 1 weight adjacent, then this adjacent has maximum distance among all vertices in dequeue (because all other vertices are either adjacent of currently popped vertex or adjacent of previously popped vertices).
Below is the implementation of the above idea. 
 

C++




// C++ program to implement single source
// shortest path for a Binary Graph
#include<bits/stdc++.h>
using namespace std;
 
/* no.of vertices */
#define V 9
 
// a structure to represent edges
struct node
{
    // two variable one denote the node
    // and other the weight
    int to, weight;
};
 
// vector to store edges
vector <node> edges[V];
 
// Prints shortest distance from given source to
// every other vertex
void zeroOneBFS(int src)
{
    // Initialize distances from given source
    int dist[V];
    for (int i=0; i<V; i++)
        dist[i] = INT_MAX;
 
    // double ende queue to do BFS.
    deque <int> Q;
    dist[src] = 0;
    Q.push_back(src);
 
    while (!Q.empty())
    {
        int v = Q.front();
        Q.pop_front();
 
        for (int i=0; i<edges[v].size(); i++)
        {
            // checking for the optimal distance
            if (dist[edges[v][i].to] > dist[v] + edges[v][i].weight)
            {
                dist[edges[v][i].to] = dist[v] + edges[v][i].weight;
 
                // Put 0 weight edges to front and 1 weight
                // edges to back so that vertices are processed
                // in increasing order of weights.
                if (edges[v][i].weight == 0)
                    Q.push_front(edges[v][i].to);
                else
                    Q.push_back(edges[v][i].to);
            }
        }
    }
 
    // printing the shortest distances
    for (int i=0; i<V; i++)
        cout << dist[i] << " ";
}
 
void addEdge(int u, int v, int wt)
{
   edges[u].push_back({v, wt});
   edges[v].push_back({u, wt});
}
 
// Driver function
int main()
{
    addEdge(0, 1, 0);
    addEdge(0, 7, 1);
    addEdge(1, 7, 1);
    addEdge(1, 2, 1);
    addEdge(2, 3, 0);
    addEdge(2, 5, 0);
    addEdge(2, 8, 1);
    addEdge(3, 4, 1);
    addEdge(3, 5, 1);
    addEdge(4, 5, 1);
    addEdge(5, 6, 1);
    addEdge(6, 7, 1);
    addEdge(7, 8, 1);
    int src = 0;//source node
    zeroOneBFS(src);
    return 0;
}

Java



// Java Program to implement 0-1 BFS
import java.util.ArrayDeque;
import java.util.ArrayList;
import java.util.Deque;
 
public class ZeroOneBFS {
    private static class Node {
        int to; // the ending vertex
        int weight; // the weight of the edge
         
        public Node(int to, int wt) {
            this.to = to;
            this.weight = wt;
        }
    }
     
    private static final int numVertex = 9;
    private ArrayList<Node>[] edges = new ArrayList[numVertex];
     
    public ZeroOneBFS() {
        for (int i = 0; i < edges.length; i++) {
            edges[i] = new ArrayList<Node>();
        }
    }
     
    public void addEdge(int u, int v, int wt) {
        edges[u].add(edges[u].size(), new Node(v, wt));
        edges[v].add(edges[v].size(), new Node(u, wt));
    }
     
    public void zeroOneBFS(int src) {
 
        // initialize distances from given source
        int[] dist = new int[numVertex];
        for (int i = 0; i < numVertex; i++) {
            dist[i] = Integer.MAX_VALUE;
        }
         
        // double ended queue to do BFS
        Deque<Integer> queue = new ArrayDeque<Integer>();
        dist[src] = 0;
        queue.addLast(src);
         
        while (!queue.isEmpty()) {
            int v = queue.removeFirst();
            for (int i = 0; i < edges[v].size(); i++) {
 
                // checking for optimal distance
                if (dist[edges[v].get(i).to] >
                        dist[v] + edges[v].get(i).weight) {
 
                    // update the distance
                    dist[edges[v].get(i).to] =
                          dist[v] + edges[v].get(i).weight;
 
                    // put 0 weight edges to front and 1
                    // weight edges to back so that vertices
                    // are processed in increasing order of weight
                    if (edges[v].get(i).weight == 0) {
                        queue.addFirst(edges[v].get(i).to);
                    } else {
                        queue.addLast(edges[v].get(i).to);
                    }
                }
            }
        }
         
        for (int i = 0; i < dist.length; i++) {
            System.out.print(dist[i] + " ");
        }
    }
     
    public static void main(String[] args) {
        ZeroOneBFS graph = new ZeroOneBFS();
        graph.addEdge(0, 1, 0);
        graph.addEdge(0, 7, 1);
        graph.addEdge(1, 7, 1);
        graph.addEdge(1, 2, 1);
        graph.addEdge(2, 3, 0);
        graph.addEdge(2, 5, 0);
        graph.addEdge(2, 8, 1);
        graph.addEdge(3, 4, 1);
        graph.addEdge(3, 5, 1);
        graph.addEdge(4, 5, 1);
        graph.addEdge(5, 6, 1);
        graph.addEdge(6, 7, 1);
        graph.addEdge(7, 8, 1);
        int src = 0;//source node
        graph.zeroOneBFS(src);
        return;
    }
}
Python3



# Python3 program to implement single source
# shortest path for a Binary Graph
from sys import maxsize as INT_MAX
from collections import deque
 
# no.of vertices
V = 9
 
# a structure to represent edges
class node:
    def __init__(self, to, weight):
 
        # two variable one denote the node
        # and other the weight
        self.to = to
        self.weight = weight
 
# vector to store edges
edges = [0] * V
for i in range(V):
    edges[i] = []
 
# Prints shortest distance from
# given source to every other vertex
def zeroOneBFS(src: int):
 
    # Initialize distances from given source
    dist = [0] * V
    for i in range(V):
        dist[i] = INT_MAX
 
    # double ende queue to do BFS.
    Q = deque()
    dist[src] = 0
    Q.append(src)
 
    while Q:
        v = Q[0]
        Q.popleft()
 
        for i in range(len(edges[v])):
 
            # checking for the optimal distance
            if (dist[edges[v][i].to] >
                dist[v] + edges[v][i].weight):
                dist[edges[v][i].to] = dist[v] + edges[v][i].weight
 
                # Put 0 weight edges to front and 1 weight
                # edges to back so that vertices are processed
                # in increasing order of weights.
                if edges[v][i].weight == 0:
                    Q.appendleft(edges[v][i].to)
                else:
                    Q.append(edges[v][i].to)
 
    # printing the shortest distances
    for i in range(V):
        print(dist[i], end = " ")
    print()
 
def addEdge(u: int, v: int, wt: int):
    edges[u].append(node(v, wt))
    edges[u].append(node(v, wt))
 
# Driver Code
if __name__ == "__main__":
 
    addEdge(0, 1, 0)
    addEdge(0, 7, 1)
    addEdge(1, 7, 1)
    addEdge(1, 2, 1)
    addEdge(2, 3, 0)
    addEdge(2, 5, 0)
    addEdge(2, 8, 1)
    addEdge(3, 4, 1)
    addEdge(3, 5, 1)
    addEdge(4, 5, 1)
    addEdge(5, 6, 1)
    addEdge(6, 7, 1)
    addEdge(7, 8, 1)
 
    # source node
    src = 0
    zeroOneBFS(src)
 
# This code is contributed by
# sanjeev2552
Javascript



<script>
// Javascript Program to implement 0-1 BFS
 
class Node
{
    constructor(to,wt)
    {
        this.to = to;
            this.weight = wt;
    }
     
}
 
let numVertex = 9;
let edges = new Array(numVertex);
 
function _ZeroOneBFS()
{
    for (let i = 0; i < edges.length; i++) {
            edges[i] = [];
        }
}
 
function addEdge(u,v,wt)
{
    edges[u].push(edges[u].length, new Node(v, wt));
        edges[v].push(edges[v].length, new Node(u, wt));
}
 
function zeroOneBFS(src)
{
    // initialize distances from given source
        let dist = new Array(numVertex);
        for (let i = 0; i < numVertex; i++) {
            dist[i] = Number.MAX_VALUE;
        }
           
        // double ended queue to do BFS
        let queue = [];
        dist[src] = 0;
        queue.push(src);
           
        while (queue.length!=0) {
            let v = queue.shift();
            for (let i = 0; i < edges[v].length; i++) {
   
                // checking for optimal distance
                if (dist[edges[v][i].to] >
                        dist[v] + edges[v][i].weight) {
   
                    // update the distance
                    dist[edges[v][i].to] =
                          dist[v] + edges[v][i].weight;
   
                    // put 0 weight edges to front and 1
                    // weight edges to back so that vertices
                    // are processed in increasing order of weight
                    if (edges[v][i].weight == 0) {
                        queue.unshift(edges[v][i].to);
                    } else {
                        queue.push(edges[v][i].to);
                    }
                }
            }
        }
           
        for (let i = 0; i < dist.length; i++) {
            document.write(dist[i] + " ");
        }
}
 
_ZeroOneBFS();
addEdge(0, 1, 0);
addEdge(0, 7, 1);
addEdge(1, 7, 1);
addEdge(1, 2, 1);
addEdge(2, 3, 0);
addEdge(2, 5, 0);
addEdge(2, 8, 1);
addEdge(3, 4, 1);
addEdge(3, 5, 1);
addEdge(4, 5, 1);
addEdge(5, 6, 1);
addEdge(6, 7, 1);
addEdge(7, 8, 1);
let src = 0;//source node
zeroOneBFS(src);
 
// This code is contributed by avanitrachhadiya2155
</script>
Output: 
 
0 0 1 1 2 1 2 1 2 
This problem can also be solved by Dijkstra but the time complexity will be O(E + V Log V) whereas by BFS it will be O(V+E).
Reference : 
http://codeforces.com/blog/entry/22276
This article is contributed by Ayush Jha. If you like GeeksforGeeks and would like to contribute, you can also write an article using write.geeksforgeeks.org or mail your article to review-team@geeksforgeeks.org. See your article appearing on the GeeksforGeeks main page and help other Geeks.
Please write comments if you find anything incorrect, or you want to share more information about the topic discussed above.
 

My Personal Notes
arrow_drop_up
Previous
Combinatorial Game Theory | Set 1 (Introduction)
Next

Trie | (Insert and Search)
Recommended Articles
Page :
Shortest Path in a weighted Graph where weight of an edge is 1 or 2
13, Mar 16
Difference between the shortest and second shortest path in an Unweighted Bidirectional Graph
04, Aug 21
Shortest distance between two nodes in Graph by reducing weight of an edge by half
12, Aug 21
Check if alternate path exists from U to V with smaller individual weight in a given Graph
28, Feb 20
Path from a given source to a given destination having Kth largest weight in a Graph
17, Mar 21
Shortest path from source to destination such that edge weights along path are alternatively increasing and decreasing
24, Apr 19
Shortest path in an unweighted graph
10, Apr 18
Multi Source Shortest Path in Unweighted Graph
07, Jun 18
Check if given path between two nodes of a graph represents a shortest paths
28, Nov 19
Shortest path in a graph from a source S to destination D with exactly K edges for multiple Queries
14, Feb 20
Shortest path with exactly k edges in a directed and weighted graph | Set 2
31, Jan 20
Shortest path in a directed graph by Dijkstra’s algorithm
12, Jun 20
Building an undirected graph and finding shortest path using Dictionaries in Python
20, Jun 20
Shortest path in a complement graph
02, Jul 20
Create a Graph by connecting divisors from N to M and find shortest path
24, Aug 20
Detect a negative cycle in a Graph using Shortest Path Faster Algorithm
30, Sep 20
1st to Kth shortest path lengths from node 1 to N in given Graph
12, Jul 21
Multistage Graph (Shortest Path)
17, Apr 18
Shortest Path in Directed Acyclic Graph
13, May 13
Shortest path with exactly k edges in a directed and weighted graph
19, Aug 14
Finding the path from one vertex to rest using BFS
16, Jan 19
Check if a given directed graph is strongly connected | Set 2 (Kosaraju using BFS)
21, Feb 17
Detect cycle in an undirected graph using BFS
02, Aug 18
Detect Cycle in a Directed Graph using BFS
28, Nov 18
Article Contributed By :
https://media.geeksforgeeks.org/auth/avatar.png
GeeksforGeeks
Vote for difficulty
Current difficulty :
Medium





Improved By :
Article Tags :
Practice Tags :
Report Issue

We use cookies to ensure you have the best browsing experience on our website. By using our site, you
acknowledge that you have read and understood our
Cookie Policy &
        Privacy Policy

Lightbox

Start Your Coding Journey Now!