Count number of paths whose weight is exactly X and has at-least one edge of weight M
Last Updated :
13 Sep, 2022
Given an infinite tree and three numbers N, M, and X which has exactly N child from every node. Every edge has a weight of 1, 2, 3, 4..N. The task is to find the count of paths whose weight is exactly X and has a minimum of one edge of weight M in it.
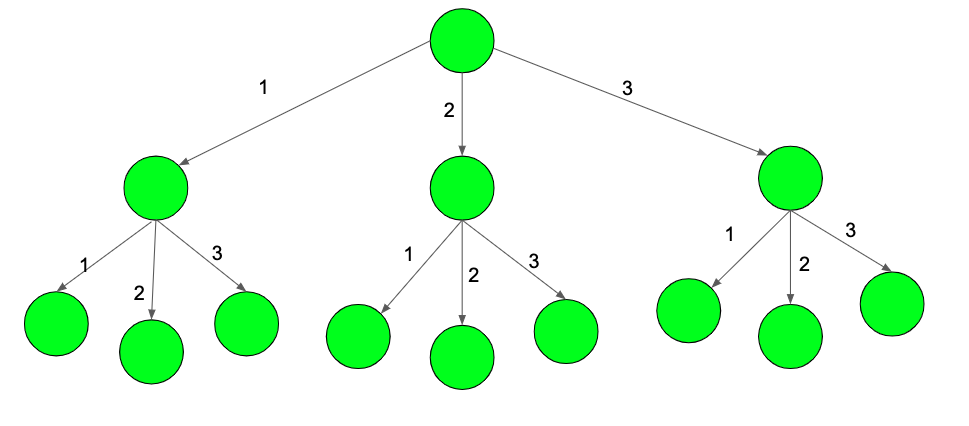
The diagram above shows a tree shown till level-3 and N = 3.
Examples:
Input: N = 3, M = 2, X = 3
Output: 2
The path 1-2 and 2-1 in the image above
Input: N = 2, M = 1, X = 4
Output: 4
Approach: The problem can be solved using Dynamic Programming and memoization. We will use a top-down approach to solve this problem. Recur starting from the root with the sum initially as X, and recursively traverse all paths possible( which is from 1 to N). If the node is equal to M, then the second parameter becomes true, else it stays the same which has been passed in the previous call. Store the value in a DP[][] table to avoid visiting the same states twice.
Below is the implementation of the above approach.
C++
#include <bits/stdc++.h>
using namespace std;
#define max 4
#define c 2
int countPaths(int sum, int get, int m, int n, int dp[])
{
if (sum < 0)
return 0;
if (sum == 0)
return get;
if (dp[sum][get] != -1)
return dp[sum][get];
int res = 0;
for (int i = 1; i <= n; i++) {
if (i == m)
res += countPaths(sum - i, 1, m, n, dp);
else
res += countPaths(sum - i, get, m, n, dp);
}
dp[sum][get] = res;
return dp[sum][get];
}
int main()
{
int n = 3, m = 2, x = 3;
int dp[max + 1];
for (int i = 0; i <= max; i++)
for (int j = 0; j < 2; j++)
dp[i][j] = -1;
cout << countPaths(x, 0, m, n, dp);
}
|
Java
public class GFG{
static int max = 4 ;
static int c = 2 ;
static int countPaths(int sum, int get, int m, int n, int dp[][])
{
if (sum < 0)
return 0;
if (sum == 0)
return get;
if (dp[sum][get] != -1)
return dp[sum][get];
int res = 0;
for (int i = 1; i <= n; i++) {
if (i == m)
res += countPaths(sum - i, 1, m, n, dp);
else
res += countPaths(sum - i, get, m, n, dp);
}
dp[sum][get] = res;
return dp[sum][get];
}
public static void main(String []args)
{
int n = 3, m = 2, x = 3;
int dp[][] = new int[max + 1][2];
for (int i = 0; i <= max; i++)
for (int j = 0; j < 2; j++)
dp[i][j] = -1;
System.out.println(countPaths(x, 0, m, n, dp));
}
}
|
Python3
Max = 4
c = 2
def countPaths(Sum, get, m, n, dp):
if (Sum < 0):
return 0
if (Sum == 0):
return get
if (dp[Sum][get] != -1):
return dp[Sum][get]
res = 0
for i in range(1, n + 1):
if (i == m):
res += countPaths(Sum - i, 1, m, n, dp)
else:
res += countPaths(Sum - i, get, m, n, dp)
dp[Sum][get] = res
return dp[Sum][get]
n = 3
m = 2
x = 3
dp = [[-1 for i in range(2)]
for i in range(Max + 1)]
for i in range(Max + 1):
for j in range(2):
dp[i][j] = -1
print(countPaths(x, 0, m, n, dp))
|
C#
using System;
class GFG
{
static int max = 4 ;
static int c = 2 ;
static int countPaths(int sum, int get, int m,
int n, int[, ] dp)
{
if (sum < 0)
return 0;
if (sum == 0)
return get;
if (dp[sum, get] != -1)
return dp[sum, get];
int res = 0;
for (int i = 1; i <= n; i++)
{
if (i == m)
res += countPaths(sum - i, 1, m, n, dp);
else
res += countPaths(sum - i, get, m, n, dp);
}
dp[sum, get] = res;
return dp[sum, get];
}
public static void Main()
{
int n = 3, m = 2, x = 3;
int[,] dp = new int[max + 1, 2];
for (int i = 0; i <= max; i++)
for (int j = 0; j < 2; j++)
dp[i, j] = -1;
Console.WriteLine(countPaths(x, 0, m, n, dp));
}
}
|
PHP
<?php
$max = 4;
$c = 2;
function countPaths($sum, $get, $m, $n, &$dp)
{
global $max,$c;
if ($sum < 0)
return 0;
if ($sum == 0)
return $get;
if ($dp[$sum][$get] != -1)
return $dp[$sum][$get];
$res = 0;
for ($i = 1; $i <= $n; $i++)
{
if ($i == $m)
$res += countPaths($sum - $i, 1, $m, $n, $dp);
else
$res += countPaths($sum - $i, $get, $m, $n, $dp);
}
$dp[$sum][$get] = $res;
return $dp[$sum][$get];
}
$n = 3;
$m = 2;
$x = 3;
$dp = array_fill(0,$max + 1,NULL);
for ($i = 0; $i <= $max; $i++)
for ($j = 0; $j < 2; $j++)
$dp[$i][$j] = -1;
echo countPaths($x, 0, $m, $n, $dp);
?>
|
Javascript
<script>
let max = 4;
let c = 2;
function countPaths(sum, get, m, n, dp)
{
if (sum < 0)
return 0;
if (sum == 0)
return get;
if (dp[sum][get] != -1)
return dp[sum][get];
let res = 0;
for(let i = 1; i <= n; i++)
{
if (i == m)
res += countPaths(sum - i, 1,
m, n, dp);
else
res += countPaths(sum - i, get,
m, n, dp);
}
dp[sum][get] = res;
return dp[sum][get];
}
let n = 3, m = 2, x = 3;
let dp = new Array(max + 1);
for(let i = 0; i <= max; i++)
{
dp[i] = new Array(2)
for(let j = 0; j < 2; j++)
dp[i][j] = -1;
}
document.write(countPaths(x, 0, m, n, dp));
</script>
|
Complexity Analysis:
- Time Complexity: O(x*n), as we are using a loop to traverse n times and in each traversal, we are recursively calling the function again which will cost O(x). Where n is the number of children from every node and x is the total weight.
- Auxiliary Space: O(x*n), as we are using extra space for the DP matrix. Where n is the number of children from every node and x is the total weight.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...