How to find the Determinant of a Matrix?

In mathematics, a matrix is a rectangle or square-shaped array of numbers or symbols grouped in rows and columns to represent a mathematical object or one of its qualities. For example, 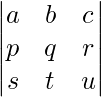 is a square matrix. On the other hand,  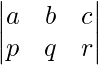is a rectangular matrix.

Determinant of a Matrix

The matrix determinant is the product of the components of any row or column and their respective co-factors. They only exist for square matrices, i.e. the ones which have an equal number of rows and columns. The determinant of any square matrix A is represented by detA (or) |A|. It is sometimes represented by the sign. Calculating the determinants of 1 × 1 and 2 × 2 matrices is very straightforward, but the procedure becomes more complicated as the rank of the matrix grows. Minors and co-factors are involved in the process of determining the determinant of a matrix.

Properties of Determinant

1. The determinant of a matrix and its own transpose are always equal, i.e., 
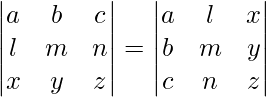
2. Interchanging any two rows or columns of a matrix would change the sign of its determinant, i.e., .
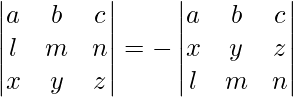3. The determinant of a matrix with any two identical rows or columns is zero, i.e., .
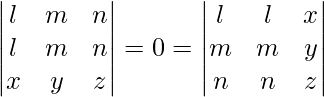4. The determinant of a matrix with zeroes as the elements of any one of its rows or columns is zero, i.e., 
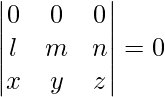
5. Multiplying each row of a determinant with a constant m would increase the value of the determinant to m times as well, i.e., .

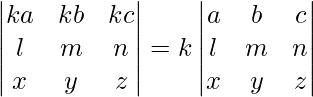• Determinant of 1 × 1 Matrix

A 1 × 1 matrix is a row with only one row and one column, and hence only one element. The determinant of every 1 × 1 matrix is always equal to the matrix element.

Example: If matrix A = [69]_{1 × 1}, then det A or |A| = 69.

• Determinant of a 2 × 2 Matrix

Given matrix A = 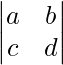 then its determinant is given by ad – bc. It is simply calculated by cross multiplying the components from top left to bottom right and then finding the difference of the two.

Example: Evaluate,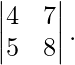

Here, a = 4, b = 7, c = 5 and d = 8. 

Hence, |A| = 4(8) – 5(7)

|A| = −3

• Determinant of a 3 × 3 Matrix

In order to find the determinant of 3 × 3 matrices, we need to understand the term minor of an element,

Minor of an Element

The determinant of a square matrix of any order derived by deleting the row and column containing the element is the minor of the element.

Example: Find the minor of 6 in the matrix 

Solution:

Since 6 lies in the second row and third column of the given matrix, its matrix would be equal to the determinant of the matrix obtained by removing the second row and the third column.

Minor of 6 = 

= 8 × 1 – 2 × 7

= 8 – 14 

= -6

The following steps are to be followed, 

1. Select any row or column. To find the determinant, we normally start with the first row.
2. Determine the co-factors of each of the row/column items that we picked in Step 1.
3. Multiply the row/column items from Step 1 by the appropriate co-factors from Step 2.
4. Add all of the products from Step 3 to get the matrix’s determinant.

Alternatively, the following formula can also be used for this purpose:

|A| =  a(ei − fh) − b(di − fg) + c(dh − eg)

Sample Problems

Question 1. Find the minor of 9 in the matrix .

Solution:

Since 9 lies in the third row and third column of the given matrix, its matrix would be equal to the determinant of the matrix obtained by removing the third row and the third column.

Minor of 9 = 

= 1 × 5 – 2 × 4

= 5 – 8

= -3

Question 2. Find the value of |4A| if A = .

Solution:

A = 

Thus, 4A = 

Now, |4A| = 4 (128 – 96) – 4 (64 – 0) – 4 (48 – 0)

= 4(32) – 4(64) – 4(48)

|4A| = -320

Question 3: Find x if the determinant of the matrix  is 0.

Solution:

Given: A = 

|A| = 4(x) – 8(2)

= 4x – 16

Since |A| = 0.

⇒ 4x – 16 = 0

or, 4x = 16

⇒ x = 4

Question 4: Evaluate: . Use properties of determinants.

Solution:

Clearly, the elements of the third row have 3 as a common factor. It can be depicted as:

Since the first and third rows of the given matrix are equal now, using the third property the value of the matrix would be zero.

|A| = 3 × 0

|A| = 0

Question 5: Find the value of (a² + b² – c²)|A| if A = .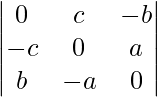

Solution:

|A| = 0(0(0) – a(a)) – c(0(-c) – a(b)) + (-b)((-c)(-a) – 0(b))

= 0 × (a²) − c(0 − ab) − b(ac – 0)

= 0

Hence, (a² + b² – c²)|A| = (a² + b² – c²)(0)

⇒ (a² + b² – c²)|A| = 0

Question 6: Find t if the determinant of the matrix  is 10.

Solution:

Given: A = 

|A| = 3(0) – 5(x)

= 0 – 5x

= -5x

Since |A| = 10.

⇒ -5x = 10

⇒ x = -2

Question 7: Find x if the determinant of the matrix  is 12.

Solution:

Given: A = 

|A| = 5(x) – 3(1)

= 5x – 3

Since |A| = 12

⇒ 5x – 3 = 12

⇒ 5x = 15

⇒ x = 3

Question 8: Evaluate: 

Solution:

Here, a = 1, b = 2, c = 3, d = 4, e = 5, f = 6, g = 7, h = 8, i = 9.

Thus, |A| = 1(5(9) – 6(8)) – 2(4(9) – 6(7)) + 3(4(8) – 5(7))

= 1(45 – 42) – 2(36 – 42) + 3(32 – 35)

= 1(3) – 2(-6) + 3(-3)

= 3 + 12 – 9

⇒ |A| = 0