Solved Examples on Dynamics of Circular Motion

Many of the motions happening around us have a circular nature. From a fan on the ceiling to a hand of a clock doing circles. These motions surround every aspect of daily lives. To understand the motion and predict the motion of the bodies in such motion. It is essential to study the dynamics of circular motion, these dynamics include the equations for force, acceleration, and velocity which govern this motion. Let’s look at these concepts in detail. 

Circular Motion

An object moving in a circular trajectory around a point is said to be performing a circular motion. For example — roughly speaking, a vehicle going on a turn is also an example of a body following a circular motion. The circular motion if continued is periodic in nature. Periodic motions are the motions that repeat themselves after a certain period of time. Based on the velocity and the acceleration, this motion can be classified into two categories – 

1. Uniform Circular Motion: When a body moves at constant speed in a circular motion along the circumference of the circular trajectory, it is called Uniform Circular Motion.
2. Non-Uniform circular motion: When a body moves in a circular motion along the circumference of a circular trajectory in such a way that its speed keeps changing. It is called a non-uniform circular motion.

Dynamics of Circular Motion

Let’s assume a circular motion in which the body is moving at a constant speed. Denoting the radius of the circular trajectory on which the body is moving by “r”, and the speed of the body by v m/s. The figure shows the body going from point A to point B in time “t”. The length of the arc from point A to point B is denoted by “s”. In this, the angle covered by the object is given by,

θ = PQ/r

θ = s/r

Angular velocity of the body is defined as the rate of change of angle. It’s similar to velocity in the case of straight-line motion.  It is denoted by the Greek symbol ω.

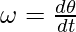
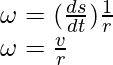
Centripetal Force

In the case of a uniform circular motion, the bodies travel with a constant velocity. Usually, Bodies have a tendency to move in a straight line. For the bodies making a circular motion at a constant speed, there must be some force that keeps them on a circular path. Such a force is called the centripetal force. The reaction of this force is called centrifugal force. This means that both these forces are equal and opposite in direction. 

Centrifugal force is given by, 

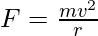
It is known that, ω = v\r

Substituting this relation into the equation,

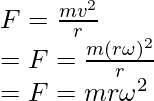
Sample Problems

Question 1: Find the angular velocity of a body that is moving at a speed of 50m/s in a circle of radius 5 m. 

Answer: 

The formula for angular velocity is given by, 

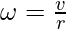
Given: v = 50m/s and r = 5 m. 

Plugging the values into the equation, 

ω = vr 

⇒ ω = (50)(5)

⇒ ω = 250 rad/s

Question 2: Find the angular velocity of a body that is moving at a speed of 10m/s in a circle of radius 8 m. 

Answer: 

The formula for angular velocity is given by, 

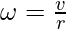
Given: v = 10m/s and r = 8 m. 

Plugging the values into the equation, 

ω = vr 

⇒ ω = (10)(8)

⇒ ω = 80 rad/s

Question 3: Find the force acting on a particle of mass 4Kg moving in a circle of radius 4 m at a speed of 5 m/s. 

Answer: 

The formula for centripetal force is given by, 

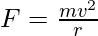
Given: v = 5 m/s, r = 4 m and m = 4Kg

Plugging the values into the equation, 

⇒ 

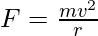
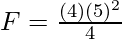
⇒ F = 25N

Question 4: Find the force acting on a particle of mass 8Kg moving in a circle of radius 5 m at a speed of 5 m/s. 

Answer: 

The formula for centripetal force is given by, 

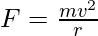
Given: v = 5 m/s, r = 5m and m = 8Kg

Plugging the values into the equation, 

⇒

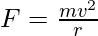
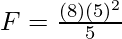
⇒ F = 40N

Question 5: Find the force acting on a particle of mass 10Kg moving in a circle of radius 8 m at an angular speed of 40 rad/s. 

Answer: 

The formula for centripetal force is given by, 

F = mrω²

Given: ω = 40, r = 8 m and m = 10Kg

Plugging the values into the equation, 

F = mrω²

⇒ F = (10)(8)(40)²

⇒ F = (80)(1600)

⇒ F = 128000 N

Question 6: Find the force acting on a particle of mass 10Kg moving in a circle of radius 8 m at an angular speed of 40 rad/s. 

Answer: 

The formula for centripetal force is given by, 

F = mrω²

Given: ω = 40, r = 8 m and m = 10Kg

Plugging the values into the equation, 

F = mrω²

⇒ F = (10)(8)(40)²

⇒ F = (80)(1600)

⇒ F = 128000 N

Question 7: An insect moves in a circle of 4 m radius and completes 20 revolutions per second. Find the angular velocity, linear velocity, and acceleration. 

Answer: 

The body moves at 20 revolutions per second. 

ω = (Angle covered per second) 

⇒ ω = (20 × 2π) = 40π

The angular velocity is 40π rad/s. 

The linear velocity is given by, 

v = rω

Given: r = 2 m

v = rω

⇒ v = (2)(40π)

⇒ v = 80π

Acceleration will be given by, 

a =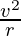 

⇒ a =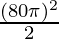 

⇒ a = 3200π² rad/s²

Question 8: An insect moves in a circle of 1 m radius and completes 10 revolutions per second. Find the angular velocity, linear velocity, and acceleration. 

Answer: 

The body moves at 10 revolutions per second. 

ω = (Angle covered per second) 

⇒ ω = (10 × 2π) = 20π

The angular velocity is 20π rad/s. 

The linear velocity is given by, 

v = rω

Given: r = 1 m

v = rω

⇒ v = (1)(20π)

⇒ v = 20π

Acceleration will be given by, 

a =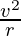 

⇒ a =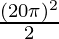 

⇒a = 200π² rad/s²