Time series analysis is one of the important methodologies that helps us to understand the hidden patterns in a dataset that is too related to the time at which it is being recorded. The article aims to explore the fundamentals of time series analysis and demonstrates the analysis using Facebook Prophet.
What is Time Series Analysis?
Time series analysis is a statistical approach that entails gathering data at consistent intervals to recognize patterns and trends. This methodology is employed for making well-informed decisions and precise forecasts by leveraging insights derived from historical data.
And the process of predicting the future values of the data by analyzing the previous trends and patterns hidden in the data is known as time series forecasting. Time series forecasting can be done using various forecasting techniques like ARIMA, SARIMA, Prophet, Theta and other statistical method. Time series data is a sequential data hence, deep learning-based methods like RNN, LSTM, BLSTM and GRU are also used for time series forecasting.
Key components of Time Series analysis
The key components of time series analysis include:
- Time series data commonly displays temporal relationships, meaning that the values at a particular moment are impacted by preceding values. Grasping these dependencies is essential for accurate predictions and gaining valuable insights.
- Trend analysis involves recognizing the fundamental direction or long-term movement in a time series, whether it is upward, downward, or stable. This understanding provides insights into the overall trajectory of the data.
- Seasonal patterns, observed in numerous time series, depict recurring cycles at fixed intervals, such as daily, monthly, quarterly, or yearly. Analyzing these patterns through seasonal analysis helps identify and comprehend their periodic nature.
- Time series data often incorporates random fluctuations or noise that lacks a specific trend or pattern. It is crucial to eliminate this noise to unveil meaningful information within the data.
Facebook Prophet Library
Prophet is an open-source tool from Facebook used for forecasting time series data which helps businesses understand and possibly predict the market. It is based on a decomposable additive model where non-linear trends fit with seasonality, it also takes into account the effects of holidays. Before we head right into coding, let’s learn certain terms that are required to understand this.
- Trend: The trend shows the tendency of the data to increase or decrease over a long period of time and it filters out the seasonal variations.
- Seasonality: Seasonality is the variations that occur over a short period of time and is not prominent enough to be called a “trend”.
Understanding the Prophet Model
The general idea of the model is similar to a generalized additive model. The “Prophet Equation” fits, as mentioned above, trends, seasonality, and holidays. This is given by,
y(t) = g(t) + s(t) + h(t) + e(t)
here,
- g(t) refers to trend (changes over a long period of time)
- s(t) refers to seasonality (periodic or short-term changes)
- h(t) refers to effects of holidays to the forecast
- e(t) refers to the unconditional changes that is specific to a business or a person or a circumstance. It is also called the error term.
- y(t) is the forecast.
Need of Facebook Prophet
We need it because, although the basic decomposable additive model looks simply, the calculation of the terms within is hugely mathematical. If you do not know what you are doing, it may lead to making wrong forecasts, which might have severe repercussions in the real world. So, to automate this process, we are going to use Prophet. However, to understand the math behind this process and how Prophet actually works, let’s see how it forecasts the data.
Prophet provides us with two models (however, newer models can be written or extended according to specific requirements).
- Logistic Growth Model
- Piece-Wise Linear Model
By default, Prophet uses a piece-wise linear model, but it can be changed by specifying the model. Choosing a model is delicate as it is dependent on a variety of factors such as company size, growth rate, business model, etc., If the data to be forecasted, has saturating and non-linear data (grows non-linearly and after reaching the saturation point, shows little to no growth or shrink and only exhibits some seasonal changes), then logistic growth model is the best option. Nevertheless, if the data shows linear properties and had growth or shrink trends in the past then, the piece-wise linear model is a better choice. The logistic growth model is fit using the following statistical equation,

where,
- C is the carrying capacity
- k is the growth rate
- m is an offset parameter
The piece-wise linear model is fit using the following statistical equations,
(1) 
where c is the trend change point (it defines the change in the trend).? is the trend parameter and can be tuned as per requirement for forecasting.
Implementation – Analyzing Time Series Data using Prophet
Now let’s try and build a model that is going to forecast the number of passengers for the next five years using time series analysis.
Installing Prophet and Other Dependencies
Install pandas for data manipulation and for the dataframe data structure.
!pip install pandas
Install Prophet for time series analysis and forecasting.
!pip install prophet
Importing Required Libraries
Python3
import pandas as pd
from prophet import Prophet
from prophet.plot import add_changepoints_to_plot
|
Loading Air Passenger Dataset
Now let’s load the csv file in the pandas data frame. The dataset contains the number of air passengers in the USA from January 1949 to December 1960. The frequency of the data is 1 month.
Python3
"/Time-Series-Analysis-and-Forecasting-of-Air-Passengers"
"/master/airpassengers.csv")
data = pd.read_csv(url)
data.head()
|
Output:
Month #Passengers
0 1949-01 112
1 1949-02 118
2 1949-03 132
3 1949-04 129
4 1949-05 121
Facebook Prophet predicts data only when it is in a certain format. The dataframe with the data should have a column saved as ds for time series data and y for the data to be forecasted. Here, the time series is the column Month and the data to be forecasted is the column #Passengers. So, let’s make a new DataFrame with new column names and the same data. Also, ds should be in a DateTime format.
Python3
df = pd.DataFrame()
df['ds'] = pd.to_datetime(data['Month'])
df['y'] = data['#Passengers']
df.head()
|
Output:
ds y
0 1949-01-01 112
1 1949-02-01 118
2 1949-03-01 132
3 1949-04-01 129
4 1949-05-01 121
Initializing a Prophet Model
By using the Prophet() command we can initialize an instance of the fbprophet model for the training on our dataset and then help us to perform time series forecasting.
We want our model to predict the next 5 years, that is, till 1965. The frequency of our data is 1 month and thus for 5 years, it is 12 * 5 = 60 months. So, we need to add 60 to more rows of monthly data to a dataframe.
Python3
future = m.make_future_dataframe(periods=12 * 5,
freq='M')
|
Now in the future dataframe we have just ds values, and we should predict the y values.
Python3
forecast = m.predict(future)
forecast[['ds', 'yhat', 'yhat_lower',
'yhat_upper', 'trend',
'trend_lower', 'trend_upper']].tail()
|
Output:
ds yhat yhat_lower yhat_upper trend trend_lower \
199 1965-07-31 723.847886 695.131427 753.432671 656.874802 649.871409
200 1965-08-31 677.972773 649.074148 707.203918 660.006451 652.869703
201 1965-09-30 640.723643 612.025440 670.377970 663.037079 655.722042
202 1965-10-31 610.965273 580.772823 641.770085 666.168728 658.710202
203 1965-11-30 640.594175 611.016447 669.582208 669.199356 661.513728
trend_upper
199 663.255178
200 666.675498
201 669.917580
202 673.241446
203 676.479915
Plotting the Forecast Data
Table ds, as we know, is the time series data. yhat is the prediction, yhat_lower, and yhat_upper are the uncertainty levels (it basically means the prediction and actual values can vary within the bounds of the uncertainty levels). Next up we have a trend that shows the long-term growth, shrink, or stagnancy of the data, trend_lower, and trend_upper is the uncertainty levels.
Python3
fig1 = m.plot(forecast, include_legend=True)
|
Output:
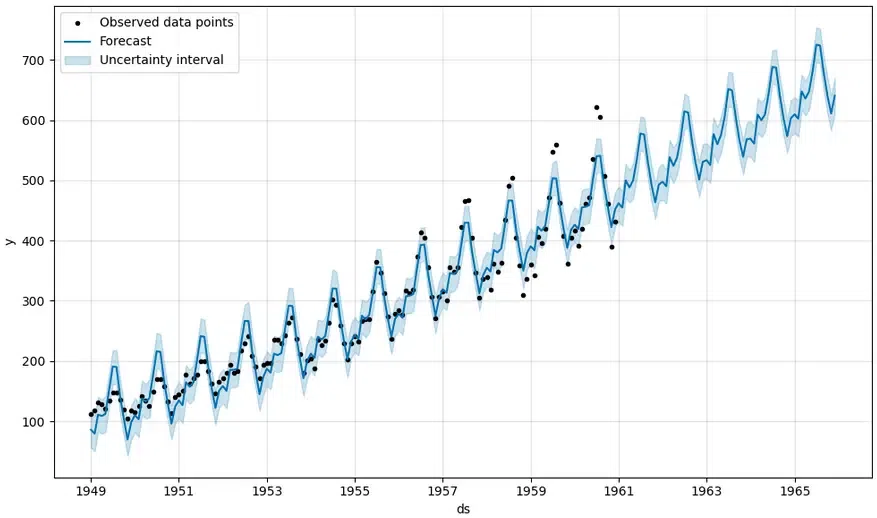
Time Series Forecasting
The below image shows the basic prediction. The light blue is the uncertainty level(yhat_upper and yhat_lower), the dark blue is the prediction(yhat) and the black dots are the original data. We can see that the predicted data is very close to the actual data. In the last five years, there is no “actual” data, but looking at the performance of our model in years where data is available it is safe to say that the predictions are close to accurate.
Python3
fig2 = m.plot_components(forecast)
|
Output:

Trends and Seasonality in Time Series Data
The below images show the trends and seasonality (in a year) of the time series data. We can see there is an increasing trend, meaning the number of air passengers has increased over time. If we look at the seasonality graph, we can see that June and July is the time with the most passengers in a given year.
Python3
fig = m.plot(forecast)
a = add_changepoints_to_plot(fig.gca(),
m, forecast)
|
Output:

Forecasting using Prophet
Add changepoints to indicate the time in rapid trend growths. The dotted red lines show the time when there was a rapid change in the trend of the passengers. Thus, we have seen how we can design a prediction model using Facebook Prophet with only a few lines of code which would have been very difficult to implement using traditional machine learning algorithms and mathematical and statistical concepts alone.
Share your thoughts in the comments
Please Login to comment...