Gated Recurrent Unit Networks

Last Updated : 23 May, 2022

Prerequisites: Recurrent Neural Networks, Long Short Term Memory Networks

To solve the Vanishing-Exploding gradients problem often encountered during the operation of a basic Recurrent Neural Network, many variations were developed. One of the most famous variations is the Long Short Term Memory Network(LSTM). One of the lesser-known but equally effective variations is the Gated Recurrent Unit Network(GRU).

Unlike LSTM, it consists of only three gates and does not maintain an Internal Cell State. The information which is stored in the Internal Cell State in an LSTM recurrent unit is incorporated into the hidden state of the Gated Recurrent Unit. This collective information is passed onto the next Gated Recurrent Unit. The different gates of a GRU are as described below:-

Update Gate(z): It determines how much of the past knowledge needs to be passed along into the future. It is analogous to the Output Gate in an LSTM recurrent unit.
Reset Gate(r): It determines how much of the past knowledge to forget. It is analogous to the combination of the Input Gate and the Forget Gate in an LSTM recurrent unit.
Current Memory Gate( 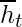$\overline{h}_{t}$ ): It is often overlooked during a typical discussion on Gated Recurrent Unit Network. It is incorporated into the Reset Gate just like the Input Modulation Gate is a sub-part of the Input Gate and is used to introduce some non-linearity into the input and to also make the input Zero-mean. Another reason to make it a sub-part of the Reset gate is to reduce the effect that previous information has on the current information that is being passed into the future.

The basic work-flow of a Gated Recurrent Unit Network is similar to that of a basic Recurrent Neural Network when illustrated, the main difference between the two is in the internal working within each recurrent unit as Gated Recurrent Unit networks consist of gates which modulate the current input and the previous hidden state.

Working of a Gated Recurrent Unit:

Take input the current input and the previous hidden state as vectors.
Calculate the values of the three different gates by following the steps given below:-
1. For each gate, calculate the parameterized current input and previously hidden state vectors by performing element-wise multiplication (Hadamard Product) between the concerned vector and the respective weights for each gate.
2. Apply the respective activation function for each gate element-wise on the parameterized vectors. Below given is the list of the gates with the activation function to be applied for the gate.

Update Gate : Sigmoid Function
Reset Gate  : Sigmoid Function

The process of calculating the Current Memory Gate is a little different. First, the Hadamard product of the Reset Gate and the previously hidden state vector is calculated. Then this vector is parameterized and then added to the parameterized current input vector.
$\overline{h}_{t} = tanh(W\odot x_{t}+W\odot (r_{t}\odot h_{t-1}))$
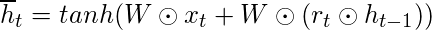
To calculate the current hidden state, first, a vector of ones and the same dimensions as that of the input is defined. This vector will be called ones and mathematically be denoted by 1. First, calculate the Hadamard Product of the update gate and the previously hidden state vector. Then generate a new vector by subtracting the update gate from ones and then calculate the Hadamard Product of the newly generated vector with the current memory gate. Finally, add the two vectors to get the currently hidden state vector.
$h_{t} = z_{t}\odot h_{t-1} + (1-z_{t})\odot \overline{h}_{t}$
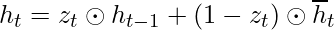
The above-stated working is stated as below:-

Note that the blue circles denote element-wise multiplication. The positive sign in the circle denotes vector addition while the negative sign denotes vector subtraction(vector addition with negative value). The weight matrix W contains different weights for the current input vector and the previous hidden state for each gate.

Just like Recurrent Neural Networks, a GRU network also generates an output at each time step and this output is used to train the network using gradient descent.

Note that just like the workflow, the training process for a GRU network is also diagrammatically similar to that of a basic Recurrent Neural Network and differs only in the internal working of each recurrent unit.

The Back-Propagation Through Time Algorithm for a Gated Recurrent Unit Network is similar to that of a Long Short Term Memory Network and differs only in the differential chain formation.

Let 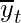$\overline{y}_{t}$ be the predicted output at each time step and 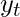$y_{t}$ be the actual output at each time step. Then the error at each time step is given by:-

$E_{t} = -y_{t}log(\overline{y}_{t})$

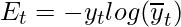
The total error is thus given by the summation of errors at all time steps.

$E = \sum _{t} E_{t}$
$\Rightarrow E = \sum _{t} -y_{t}log(\overline{y}_{t})$

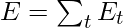
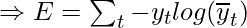
Similarly, the value 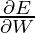$\frac{\partial E}{\partial W}$ can be calculated as the summation of the gradients at each time step.

$\frac{\partial E}{\partial W} = \sum _{t} \frac{\partial E_{t}}{\partial W}$

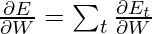
Using the chain rule and using the fact that 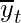$\overline{y}_{t}$ is a function of 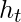$h_{t}$ and which indeed is a function of 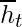$\overline{h}_{t}$ , the following expression arises:-

$\frac{\partial E_{t}}{\partial W} = \frac{\partial E_{t}}{\partial \overline{y}_{t}}\frac{\partial \overline{y}_{t}}{\partial h_{t}}\frac{\partial h_{t}}{\partial h_{t-1}}\frac{\partial h_{t-1}}{\partial h_{t-2}}......\frac{\partial h_{0}}{\partial W}$

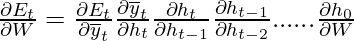
Thus the total error gradient is given by the following:-

$\frac{\partial E}{\partial W} = \sum _{t}\frac{\partial E_{t}}{\partial \overline{y}_{t}}\frac{\partial \overline{y}_{t}}{\partial h_{t}}\frac{\partial h_{t}}{\partial h_{t-1}}\frac{\partial h_{t-1}}{\partial h_{t-2}}......\frac{\partial h_{0}}{\partial W}$

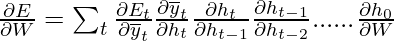
Note that the gradient equation involves a chain of 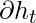$\partial {h}_{t}$ which looks similar to that of a basic Recurrent Neural Network but this equation works differently because of the internal workings of the derivatives of $h_{t}$ .

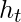How do Gated Recurrent Units solve the problem of vanishing gradients?

The value of the gradients is controlled by the chain of derivatives starting from 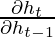$\frac{\partial h_{t}}{\partial h_{t-1}}$ . Recall the expression for $h_{t}$ :-

$h_{t} = z_{t}\odot h_{t-1} + (1-z_{t})\odot \overline{h}_{t}$

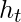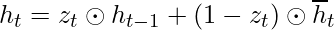
Using the above expression, the value for 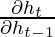$\frac{\partial {h}_{t}}{\partial {h}_{t-1}}$ is:-

$\frac{\partial h_{t}}{\partial h_{t-1}} = z + (1-z)\frac{\partial \overline{h}_{t}}{\partial h_{t-1}}$

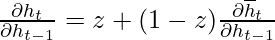
Recall the expression for 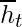$\overline{h}_{t}$ :-

$\overline{h}_{t} = tanh(W\odot x_{t}+W\odot (r_{t}\odot h_{t-1}))$

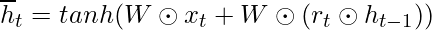
Using the above expression to calculate the value of 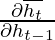$\frac{\partial \overline{h_{t}}}{\partial h_{t-1}}$ :-

$\frac{\partial \overline{h_{t}}}{\partial h_{t-1}} = \frac{\partial (tanh(W\odot x_{t}+W\odot (r_{t}\odot h_{t-1})))}{\partial h_{t-1}} \Rightarrow \frac{\partial \overline{h_{t}}}{\partial h_{t-1}} = (1-\overline{h}_{t}^{2})(W\odot r)$

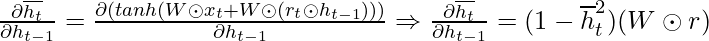
Since both the update and reset gate use the sigmoid function as their activation function, both can take values either 0 or 1.

Case 1(z = 1):

In this case, irrespective of the value of $r$ , the term $\frac{\partial \overline{h_{t}}}{\partial h_{t-1}}$ is equal to z which in turn is equal to 1.

Case 2A(z=0 and r=0):

In this case, the term 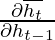$\frac{\partial \overline{h_{t}}}{\partial h_{t-1}}$ is equal to 0.

Case 2B(z=0 and r=1):

In this case, the term 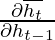$\frac{\partial \overline{h_{t}}}{\partial h_{t-1}}$ is equal to 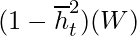$(1-\overline{h}_{t}^{2})(W)$ . This value is controlled by the weight matrix which is trainable and thus the network learns to adjust the weights in such a way that the term 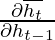$\frac{\partial \overline{h_{t}}}{\partial h_{t-1}}$ comes closer to 1.

Thus the Back-Propagation Through Time algorithm adjusts the respective weights in such a manner that the value of the chain of derivatives is as close to 1 as possible.

My Personal Notes

Related Articles

Gated Recurrent Unit Networks

Start Your Coding Journey Now!