Student’s t-distribution in Statistics
Last Updated :
23 Jan, 2024
As we know normal distribution assumes two important characteristics about the dataset: a large sample size and knowledge of the population standard deviation. However, if we do not meet these two criteria, and we have a small sample size or an unknown population standard deviation, then we use the t-distribution.
Prerequisite – Normal distribution
What is t-distribution?
Student’s t-distribution, also known as the t-distribution, is a probability distribution that is used in statistics for making inferences about the population mean when the sample size is small or when the population standard deviation is unknown. It is similar to the standard normal distribution (Z-distribution), but it has heavier tails. Theoretical work on t-distribution was done by W.S. Gosset; he has published his findings under the pen name “Student“. That’s why it is called a Student’s t-test. The t-score represents the number of standard deviations the sample mean is away from the population mean.
T-Score
The T-score, also known as the t-value or t-statistic, is a standardized score that quantifies how many standard deviations a data point or sample mean is from the population mean. It is commonly used in statistical hypothesis testing, particularly in scenarios where the sample size is small or the population standard deviation is unknown.
The formula for calculating the T-score in the context of a t-distribution is given by:

where,
- t = t-score,
- x̄ = sample mean
- μ = population mean,
- s = standard deviation of the sample,
- n = sample size
As we know, we use t-distribution when the standard deviation of the population is unknown and the sample size is small. The formula for the t-distribution looks very similar to the normal distribution; the only difference is that instead of the standard deviation of the population, we will use the standard deviation of the sample.
When to Use the t-Distribution?
Student’s t Distribution is used when :
- The sample size is 30 or less than 30.
- The population standard deviation(σ) is unknown.
- The population distribution must be unimodal and skewed.
Mathematical Derivation of t-Distribution
The t-distribution has been derived mathematically under the assumption of a normally distributed population and the formula for the probability density function will be like this
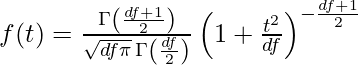
where,
- Γ(.) is the gamma function
- df= Degrees of freedom
So, this above equation indicates the probability density function(pdf) of the t-distribution for df degrees of freedom.
Significance of the t-Distribution
- Degrees of Freedom and Tail Heaviness:
The t-distribution degrees of freedom influence tail heaviness, with smaller values yielding heavier tails. Higher degrees of freedom make the t-distribution more akin to a standard normal distribution (mean 0, standard deviation 1), shaping its spread. - Small Sample Size:
The t-distribution is vital for small sample sizes, offering a precise probability distribution for statistical inferences on population parameters, especially the mean. This is crucial when the population standard deviation is unknown and must be estimated from the sample. - t-Score Calculation for Inference:
In situations where the standard deviation of the population is not known, the t-score (T) is calculated to make inferences about the population mean.The distinction between s and σ (population standard deviation) and the utilization of (n – 1) degrees of freedom delineate the characteristics of the t-distribution. - Comparison with Z-Score and Normal Distribution:
Unlike the z-score, which employs the population standard deviation, the t-score uses the estimated standard deviation from the sample. This results in a t-distribution with (n – 1) degrees of freedom, emphasizing the t-distribution’s role in handling uncertainty when estimating the population standard deviation, especially in small sample sizes.
Interpretation of t-Distribution
A confidence interval for the mean is a statistical range computed from the data, designed to encompass a plausible “population” mean. This interval is expressed as  , t represents a critical value obtained from the t-distribution.
, t represents a critical value obtained from the t-distribution.
Suppose we are investigating the mean study time for an exam by collecting data from a sample of 20 students. To establish a 90% confidence interval for the population mean study time using the above formula.
Let us say 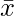 = 4 hours, s= 1.5 hours and n =20. The critical t-value is obtained for a 90% confidence interval with 19 degrees of freedom. Assuming a critical t-value of 1.729(calculated using the t table or online calculator), the calculation results in a 90% confidence interval for the average study time, such as between 3.58 hours and 4.42 hours. This utilization of the t-distribution addresses the uncertainty linked to estimating the population mean from a sample, especially in cases where the population standard deviation is unknown.
= 4 hours, s= 1.5 hours and n =20. The critical t-value is obtained for a 90% confidence interval with 19 degrees of freedom. Assuming a critical t-value of 1.729(calculated using the t table or online calculator), the calculation results in a 90% confidence interval for the average study time, such as between 3.58 hours and 4.42 hours. This utilization of the t-distribution addresses the uncertainty linked to estimating the population mean from a sample, especially in cases where the population standard deviation is unknown.
Properties of the t-Distribution
- The variable in t-distribution ranges from -∞ to +∞ (-∞ < t < +∞).
- t- distribution will be symmetric like the normal distribution if the power of t is even in the probability density function(pdf).
- For large values of ν(i.e. increased sample size n); the t-distribution tends to a standard normal distribution. This implies that for different ν values, the shape of t-distribution also differs.
- The t-distribution is less peaked than the normal distribution at the center and higher peaked in the tails. From the above diagram, one can observe that the red and green curves are less peaked at the center but higher peaked at the tails than the blue curve.
- The value of y(peak height) attains highest at μ = 0 as one can observe the same in the above diagram.
- The mean of the distribution is equal to 0 for ν > 1 where ν = degrees of freedom, otherwise undefined.
- The median and mode of the distribution is equal to 0.
- The variance is equal to ν / ν-2 for ν > 2 and ∞ for 2 < ν ≤ 4 otherwise undefined.
-min.png)
Degrees of freedom refer to the number of independent observations in a set of data. When estimating a mean score or a proportion from a single sample, the number of independent observations is equal to the sample size minus one.
Hence, the distribution of the t statistic from samples of size 10 would be described by a t distribution having 10 – 1 or 9 degrees of freedom. Similarly, a t- distribution having 15 degrees of freedom would be used with a sample of size 16.
t-Distribution Table
t-Distribution table gives the t-value for a different level of significance and different degrees of freedom. The calculated t-value will be compared with the tabulated t-value. For example, if one is performing a student’s t-test and for that performance, he has taken a 5% level of significance and he got or calculated t-value and he has taken his tabulated t-value and if the calculated t-value is higher than the tabulated t-value, in that case, it will say that there is a significant difference between the population mean and the sample means at 5% level of significance and if vice versa then, in that case, it will say that there is no significant difference between the population means and the sample means at 5% level of significance.
.webp)
T- Distribution table
t-scores and p-values
t-scores :
- It represents the deviation of a data point from the mean in a t-distribution, expressed in terms of standard deviations. Particularly useful for small sample sizes or cases with unknown population standard deviations.
- We can obtain them from a t-table or through online tools, providing a numerical measure of how atypical a data point is within the distribution.
- t-score is important in determining confidence intervals, aiding in estimating the range within which the true population parameter is likely to fall. The critical value of t is integral in confidence interval calculations, guiding the determination of upper and lower bounds.
p-value:
The p-value (probability value) is a statistical measure that helps assess the evidence against a null hypothesis.
- p-value describes the likelihood of data occurring if the null hypothesis were true.
- You can use statistical software to directly obtain the p-value associated with the calculated t-score or you can use the t-table, which provides critical values for different levels of significance and degrees of freedom. First, find the row corresponding to your degrees of freedom and the column corresponding to your t-score to get the p-value.
Limitations of Using a T-Distribution
- Sensitivity to Departure from Normality: The t-distribution assumes normality in the underlying population. When data deviates significantly from a normal distribution, reliance on the t-distribution may introduce inaccuracies in statistical inferences.
- Limited Applicability for Large Samples: As sample sizes increase, the t-distribution converges to the normal distribution. Therefore, for sufficiently large samples and known population standard deviation, the normal distribution is more appropriate, and using the t-distribution may not offer additional benefits.
- Impact of Outliers and Small Sample Sizes: The t-distribution can be sensitive to outliers, and its tails can be influenced by small sample sizes. Outliers may distort results, and in cases where the sample size is very small, the t-distribution may have heavier tails, affecting the accuracy of inferences.
- Requires Random Sampling: The assumptions underlying the t-distribution, such as random sampling and independence of observations, need to be met for valid results. If these assumptions are violated, the accuracy of inferences drawn from the t-distribution may be compromised.
T- Distribution Applications
- Testing for the Hypothesis of the Population Mean:T-distributions are commonly used in hypothesis tests regarding the population mean. This involves assessing whether a sample mean is significantly different from a hypothesized population mean.
- Testing for the Hypothesis of the Difference Between Two Means:T-tests can be employed to examine if there is a significant difference between the means of two independent samples. This can be done under the assumption of equal variances or when variances are unequal.In scenarios where samples are not independent, such as paired or dependent samples, t-tests can be used to assess the significance of the mean difference between related observations.
- Testing for the Hypothesis about the Coefficient of Correlation:T-distributions play a role in hypothesis testing related to correlation coefficients. This includes situations where the population correlation coefficient is assumed to be zero (ρ=0) or when testing for a non-zero correlation coefficient (ρ≠0).
Difference Between T-Distribution and Normal Distribution
|
| T-Distribution is defined by its degree of freedom which itself depends upon the sample size | Normal distribution is defined by its mean and standard deviation |
| T- distribution is used when the sample size is small | Normal distribution is used when we have large no data points in the dataset |
| It has a heavier tail than normal distribution which means more data points are away from the mean of the distribution | Normal distribution has a lighter tail than T-distribution which means more data points lie near the mean of the distribution |
| We use T-distribution in hypothesis testing when the standard variation of the population is unknown | Normal distribution is used when the standard deviation is known |
| T-Distribution has a larger range of critical values as compared to the normal distribution as this distribution has heavier tails | Normal distribution has a smaller range as compared to t-distribution |
We can also use Python to implement t-distribution for hypothesis testing the article regarding this could be found here.
Conclusions
The t-distribution serves as a vital tool in statistics, particularly when estimating the significance of population parameters with small sample sizes or unknown variations. While sharing the bell-shaped and symmetric characteristics of the normal distribution, the t-distribution distinguishes itself with heavier tails, introducing a higher likelihood of extreme values. Understanding its properties and applications is essential for accurate statistical inference in scenarios where the assumptions of normality and known population standard deviation are not met.
Share your thoughts in the comments
Please Login to comment...