Row Echelon Form

A matrix is in Row Echelon form if it has the following properties:

• Any row consisting entirely of zeros occurs at the bottom of the matrix.
• For each row that does not contain entirely zeros, the first non-zero entry is 1 (called a leading 1).
• For two successive (non-zero) rows, the leading 1 in the higher row is further left than the leading one in the lower row.

For reduced row echelon form, the leading 1 of every row contains 0 below and above its in that column.

Below is an example of row-echelon form: 

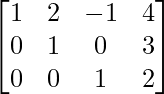
and reduced row-echelon form:

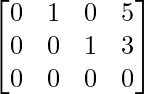
Any matrix can be transformed to reduced row echelon form, using a technique called Gaussian elimination. This is particularly useful for solving systems of linear equations.

Gaussian Elimination

Gaussian Elimination is a way of converting a matrix into the reduced row echelon form. It can also be used as a way of finding a solution to a solution to the system of linear equations. The idea behind this is that we perform some mathematical operations on the row and continue until only one variable is left.

Below are some operations which we can perform:

• Interchange any two rows
• Add two rows together.
• Multiply one row by a non-zero constant (i.e. 1/3, -1/5, 2).

Given the following linear equation:

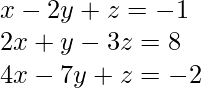
and the augmented matrix above 

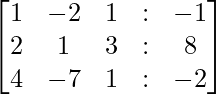
Now, we need to convert this into the row-echelon form. To convert this into row-echelon form, we need to perform Gaussian Elimination.

• First, we need to subtract 2*r₁ from the r₂ and 4*r₁ from the r₃ to get the 0 in the first place of r₂ and r₃.

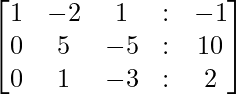
• Next, we will interchange the rows, r2 and r3 and after that subtract 5*r₂ from r₃ to get the second 0 in the third row.

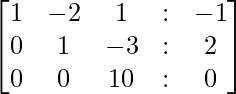
• Now, we can deduce the value z from r_3, i.e 10 z =0 ⇾ z=0. With the help of the value of z =0, we can put it to r2, y = 2. Similarly, we can put the value of y and z in r₁ and we get a value of x=3

Rank of matrix

The rank of the matrix is the number of non-zero rows in the row echelon form. To find the rank, we need to perform the following steps:

• Find the row-echelon form of the given matrix
• Count the number of non-zero rows.

Let’s take an example matrix:

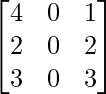
Now, we reduce the above matrix to row-echelon form

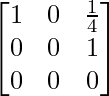
Here, only two row contains non-zero elements. Hence, the rank of the matrix is 2.

Implementation

• To convert a matrix into reduced row-echelon form, we used the Sympy package in python, first, we need to install it.

python3

# install sympy
! pip install sympy

# import sympy
import sympy

# find the reduced row echelon form
sympy.Matrix([[4,0,1],[2,0,2],[3,0,3]]).rref()

# find the rank of matrix
print("Rank of matrix :",sympy.Matrix([[4,0,1],[2,0,2],[3,0,3]]).rank())

Output:

(Matrix([
 [1, 0, 0],
 [0, 0, 1],
 [0, 0, 0]]), (0, 2))
 
 Rank of matrix : 2