Polynomials are algebraic expressions in which the power of variables is non-negative integers. They are used in various fields of mathematics, astronomy, economics, etc. There are various examples of the polynomials such as 2x + 3, x2 + 4x + 5, etc.
In this article, we will learn about, Polynomials, Degrees of Polynomials, Examples of Polynomials, Zeros of Polynomials, Polynomial Equations, and others in detail.
What are Polynomials?
A polynomial is a mathematical expression that involves variables (like x), numbers, and operations like addition, subtraction, and multiplication and the power of variables is non-negative integers. Each term consists of a variable raised to a non-negative whole number power, multiplied by a number. In the image added below, we have shown a polynomial, with variables, constants, and leading coefficient.
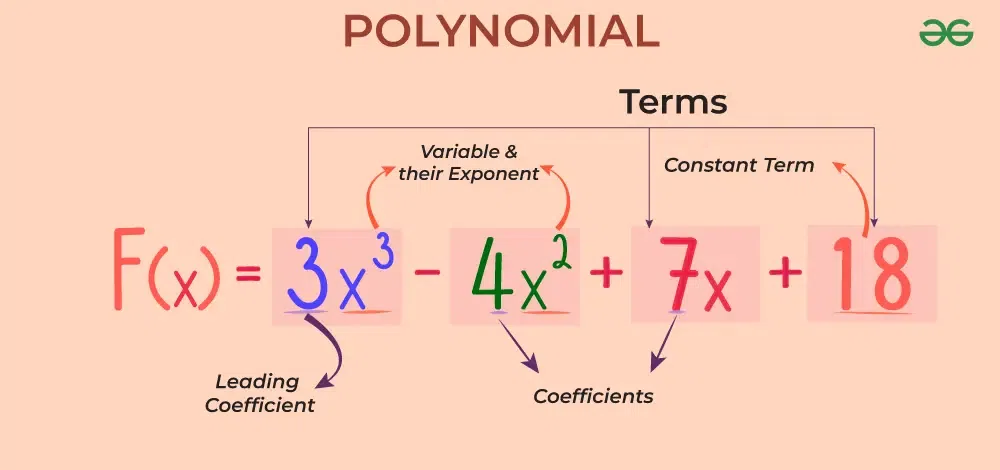
Identifying Polynomials
Example: Check whether 3x2 + 2x – 5 is polynomial or not.
Solution:
- First term is 3x2, where the variable “x” is raised to the power of 2 and multiplied by the coefficient 3.
- Second term is 2x, where the variable “x” is raised to the power of 1 (which is often omitted) and multiplied by the coefficient 2.
- Third term is -5, which does not have a variable since it is a constant term.
As all these follow the definition of polynomial. So this is a polynomial.
Polynomial Definition
Polynomial is defined as the mathematical expression that are made up of variables, constant in which the powers of variables are non negative integers. In mathematics a Polynomials is defined as,
P(x) = anxn + an-1xn-1 +an-2xn-2 + . . . + a1x + a0
where,
- x is Variable of the Polynomial
- xn, xn-1, xn-2, . . . , x are various exponents of variable
- an, an-1, an-2, . . . , a1 are Coefficeints of respective exponents of variable
- a0 is Constant Term
Polynomial Examples
Various examples of the polynomial equations are:
- 3x3 + 5x2 – 4x,
- x2 + 2x,
- 5x + y
- √2(x) + y, etc.
Characteristics of Polynomial
A polynomial can have the following characteristics:
Variables and Exponents: A polynomial consists of one or more variables, such as x or y, raised to non-negative integer exponents.
Coefficients: Coefficients are constants in the polynomial that are multiplied by the variable, These constants can be real or complex but generally these are integers or fractions.
Terms: A polynomial is composed of multiple terms, each separated by addition or subtraction operators. Each term consists of a coefficient multiplied by a variable raised to a specific exponent.
Leading Term: The leading term of a polynomial is the term with the highest degree. It determines the dominant behavior of the polynomial as the input values increase or decrease.
Constant Term: The constant term of a polynomial is a term that does not have any variables. It is the term with zero exponents, and its coefficient represents the y-intercept of the polynomial when graphed.
Standard form of a polynomial is the way of representing a polynomial in mathematics. In standard form of polynomial the terms of the polynomial are written in the descending order of their degree. The example of standard form of a polynomial is:
P(x) = anxn + an-1xn-1 +an-2xn-2 + . . . + a1x + a0
The polynomial function can be represented by P(x) where x represents the variable.
Example: Express the variable in Standard form: x2 – 3x3 + 4x
Solution:
= x2 – 3x3 + 4x
In standard form polynomial is arranged in decreasing order of their degree
= -3x3 + x2 + 4x
Degree of Polynomial
The degree of a polynomial is determined by the highest exponent or power of the variable in the expression. It represents the highest degree term in the polynomial.
To find the degree of polynomial expression there comes two cases:
Degree of Single Variable Polynomial
The degree of a single variable polynomial is determined by the highest exponent or power of that variable in the polynomial expression. It is represented by the highest degree term in the polynomial.
Example: 5x5 – 2x3 + 4x2 – x + 4
Solution:
The highest exponent is 5, which corresponds to the term 5x5. Therefore, the degree of this polynomial is 5.
Note: The degree of any polynomial which contains constant terms will be zero.
Degree of a Multivariable Polynomial
The degree of a multivariable polynomial is determined by the sum of the exponents of the variables in each term, considering the highest sum among all the terms.
Example: 5x2y3 – 2xy4 + 3x3+ 10
Solution:
In this expression, we have terms with variables x and y raised to different powers. To find the degree, we calculate the sum of the exponents for each term:
- First term, 5x2y3, has a sum of exponents equal to 2 + 3 = 5.
- Second term, -2xy4, has a sum of exponents equal to 1 + 4 = 5.
- Third term, 3x3, has a sum of exponents equal to 3.
Among all the terms the highest sum of exponents is 5. Therefore, the degree of this polynomial is 5.
Terms in a Polynomial
In a polynomial various terms are separated using the plus(+) and the minus(-) sign. Depending on the number of terms in a polynomial a polynomial can be monomial, binomial, etc.
In a polynomial we classifies various terms into like terms and unlike terms.
- Like terms are the terms that have same variable and with same exponent.
- Unlike terms are terms that have different variables or different powers(even with same variable).
For example, Identify like terms and unlike terms in the polynomial, 4x3 + 2x2 -3xy + x3 – xy
Solution:
Given Polynomial,
Like Terms: (4x3, x3) and (-3xy, -xy)
Unlike Terms: (4x3, x2), (x3, x2), (-3xy, x2), (-xy, x2), etc
Types of Polynomials
Polynomials are classified based on the number of terms they contain, and they can be divided into the following categories:
- Monomial: A polynomial with only one term is called a Monomial, and it must not be zero.
Examples: 2x, 5x3, 10
- Binomial: A polynomial with two terms is called a binomial. It can be expressed as the sum or difference of two or more monomials.
Examples: 3x4 + 4x, 5y3 + 3x, xy3 + 3y
- Trinomial: A polynomial with three terms is referred to as a trinomial.
Examples: 5x2 + 4x + 10, 10y4 + 4x4 + 2x2, 7y2 + 3y + 10
- Quadronomial: Polynomial containing 4 terms is called the Quadronomial.
Example: 3x2 + 2x + y3 – 11y, 13x3 – x + y2 – 4y, etc.
Simillarly, a polynomial can have more than four terms, i.e. it can have five terms, six terms, etc. On the basis of degree of polynomial a polynomial can be classified as:
- Zero Polynomial
- Constant Polynomial
- Linear Polynomial
- Quadratic Polynomial
- Cubic Polynomial
Now let’s learn about the same in detail.
Zero Polynomial: A polynomial with zero degree is called a Zero Polynomial. Example: 0
Constant Polynomial: A polynomial with only constant term is called a Constant Polynomial. Example: 5, 11, 9, etc.
Linear Polynomial: A polynomial with degree one is called a Linear Polynomial. Example: x + 4, y – 2z, etc.
Quadratic Polynomial: A polynomial with degree two is called a Quadratic Polynomial. Example: x2 + 2x + 3, y2, etc.
Cubic Polynomial: A polynomial with degree three is called a Cubic Polynomial. Example: x3 + 3x – 5, y3 + 4y, etc.
Apart from these we also have polynomials with degree 4, 5, and higher.
Properties of Polynomials (Theorems of Polynomials)
Various properties of the polynomials are:
For two polynomials P(x) and Q(x)
- degree (P ± Q) ≤ max(deg P, deg Q)
- deg(P⋅Q) = deg P + deg Q
For two given polynomials P(x) and Q(x) we always have unique polynomials Q (Quotient Polynomial) and R (Residue Polynomial) such that,
If a polynomial P(x) is divided by polynomial x – a, then P(a) = 0 is always true. This is also called Bezout’s Theorem or Factor Theorem.
If we a polynomial Q divides the polynomial P then zeros of polynomial Q are the zeros of polynomial P. For a polynomial of n degree we have n roots real or complex. Remainder of a polynomial f(x) when divided by (x – a) is f(a).
Polynomial Operations
There are four major polynomial operations:
- Addition of Polynomials
- Subtraction of Polynomials
- Multiplication of Polynomials
- Division of Polynomials
- Factorization of Polynomial
Addition of Polynomials
When adding polynomials, it is important to combine the like terms, which means adding the terms that have the same variable and exponent. Adding polynomials will always yield a polynomial of the same degree as the original polynomials being added.
Example: Add the polynomials 3x2 + 2x + 1 and 2x2 – 4x + 3.
Solution:
Identify like terms,
- x2 are 3x2 and 2x2 are like terms.
- x are 2x and -4x are like terms.
- Constant terms are 1 and 3.
Combining the like terms, we have and add the coefficients of the like terms
(3x2 + 2x2) + (2x – 4x) + (1 + 3)
Simplifying,
5x2 – 2x + 4
Therefore,
(3x2 + 2x + 1) + (2x2 – 4x + 3)
= 5x2 – 2x + 4
Subtraction of Polynomials
When it comes to subtracting polynomials, the process is similar to addition, but with a different operation. You subtract the like terms to find the solution. It’s important to remember that subtracting polynomials will always result in a polynomial of the same degree.
Example: Subtraction the polynomial 2x2 + 3x – 5 from the polynomial 4x2 – 2x + 7.
Solution:
(4x2 – 2x + 7) – (2x2 + 3x – 5)
= 4x2 – 2x + 7 – 2x2 – 3x + 5
= (4x2 – 2x2) + (-2x – 3x) + (7 + 5)
= 2x2 – 5x + 12
Learn more about the Addition and Subtraction of Polynomials
Multiplication of Polynomials
When two or more polynomials are multiplied together, the resulting polynomial will generally have a higher degree than the original polynomials, unless one of them is a constant polynomial.
Read More: Multiplying Polynomials
Example: Multiply the polynomials (x + 2) and (x – 3).
Solution:
= (x + 2) × (x – 3)
= x × x + x × (-3) + 2 × x + 2 × (-3)
= x2 – 3x + 2x – 6
= x2 – x – 6
Division of Polynomials
It is an arithmetic operation by which a polynomial is divided by another polynomial in a known as polynomial division. For this operation to succeed, the divisor polynomial must have a degree that is less than or equal to the dividend polynomial.
There are several ways to divide polynomials, some of which include:
- Long Division
- Synthetic Division
- Polynomial Division Using Factors
Read more about Dividing Polynomials
Factorization of Polynomials
Factorization of polynomials refers to the process of breaking down a polynomial expression into a product of simpler polynomial expressions. It involves finding the factors of the given polynomial, which are the polynomial expressions that, when multiplied together, yield the original polynomial.
Let’s first understand what factors are before learning about the techniques for factoring polynomials. Factors are just multiples of numbers that produce the initial needed number. In the same way, when it comes to polynomials, the factors are other polynomials that were multiplied together to produce the original polynomial.
Now let’s understand the numerous methods for factoring polynomials and the most used formulae for doing so.
Methods of Factorization of Polynomial
There are four different factoring polynomials formulas as follows:
- Greatest Common Factor (GCF)
- Substitution Method
- Grouping Method
- Difference of Two Squares Identity
Greatest Common Factor (GCF)
This is the basic method for factoring polynomials as Greatest Common Factor (GCF). In this method, we have to identify any common factor in all the terms. If any common factor is found then factor it out of the polynomial. It is simply a reverse procedure of the distributive law.
In the case of distributive law, we get:
a(b+c) = ab + ac
Whereas in the case of factorization, we invert the process
ab + ac = a(b+c)
Here ‘a’ is the greatest common factor.
Example: Factorize 2x2 + 4x
Solution:
= 2x2 + 4x
= 2(x2 + 2x)
Substitution Method
This method can be very helpful if a given polynomial is too complex, in such case, we have to figure it out and try substituting the complicated terms with a simpler term to solve. Therefore it makes it much easier to factor out.
Example: Factorize 3x2 + 12xy + 9y2
Solution:
Let’s substitute A = 3x and B = 3y
3x2 + 12xy + 9y2
= (A)2 + 2AB + (B)2
= A2 + 2AB + B2
= (A + B)2
= (3x + 3y)2
Grouping Method
If an expression has an even number of terms but no common factors exist for any of the terms, we can pair the terms together and get the common factor for each pair:
Example: Factorize 3x + 4ay – 3y – 4ax
Solution:
= 3x – 3y + 4ay – 4ax
= 3(x – y) + 4a(y – x)
= 3(x – y) – 4a(x – y)
= (3 – 4a)( x – y)
Difference of Two Squares Identity
This is a specific technique used when dealing with polynomials that can be expressed as the difference of two perfect squares. The identity states that the expression a2 – b2 can be factored as (a + b)(a – b).
Example: Factorize: 16x2 – 25
Solution:
= 16x2 – 25
= (4x)2 – (5)2
Comparing with a2 – b2 = (a – b)(a + b)
= (4x + 5)(4x – 5)
Zeros of Polynomial
Zeros of a polynomial, also known as roots or solutions, are the values of the variable that make the polynomial equal to zero. In other words, they are the values of x for which the polynomial evaluates to zero.
How to Find Zeros of Polynomials?
The number of zeros that a polynomial contains is determined by the degree of the polynomial equation. Polynomial equations are categorized into various types such as linear equations, quadratic equations, cubic equations, and higher-degree polynomials. Each type of equation is examined separately in order to determine the zeros of the polynomial.
Linear Polynomial
A linear polynomial is a polynomial with degree 1. The standard form is y = ax + b, where a and b are real numbers and a≠0.
Examples of linear polynomials: 2x + 3, a – 6b, y – 12, etc.
Zeroes of a Linear Polynomial
The zero of this equation can be calculated by substituting y = 0, and on simplification, we have ax + b = 0, or x = -b/a.
Quadratic Polynomial
A polynomial of degree 2 is known as a quadratic polynomial. The standard form is ax2 + bx + c, where a, b, and c are real numbers and a ≠ 0.
Examples of Quadratic Polynomials: x2+ 3x + 4, 3y2+ 7xy + 4y, etc.
Zeroes of Quadratic polynomial
Quadratic equation of the form x2 + x(a + b) + ab = 0 can be factorized as
(x + a)(x + b) = 0,
Where we have x = -a, and x = -b as the zeros of the polynomial.
And for a quadratic equation of the form ax2+ bx + c = 0, which cannot be factorized, the zeros can be calculated using the formula method, and the formula is
x = [- b ± √(b2 – 2ac) ] / 2a
Cubic Polynomial
A cubic polynomial is a polynomial of degree three. The standard form is ax3+ bx2 + cx + d, where a, b, c, and d are real numbers and a≠0.
Examples of a Cubic Polynomials: x3 + 4x2 + 7x + 2, 3y3 – 2y2+ 4y – 7, etc.
Zeroes of Cubic Polynomial
The cubic equation of the form y = ax3 + bx2 + cx + d, can be factorized by applying the remainder theorem. According to the remainder theorem, if we substitute a smaller value, denoted as α, for the variable x and the resulting value of y is zero (y = 0), then (x – α) is one of the roots of the equation. By dividing the cubic equation by (x – α) using long division, we can obtain a quadratic equation. The quadratic equation can then be solved either through factorization or by using the formula method to find the two desired roots of the equation.
Higher Degree Polynomial
The higher degree polynomial equation is of the form y = axn+ bxn – 1+cxn – 2 + ….. px + q. The remainder theorem can be used to factorize higher-degree polynomials, resulting in a quadratic equation. This quadratic equation can then be further factorized to obtain the two factors needed for the polynomial.
Learn more about the Factorization of Polynomials
Polynomial Identities
All identities of polynomials which are also called as algebraic identities are provided below:
- (a+b)2 = a2+b2+2ab
- (a-b)2 = a2+b2-2ab
- (a+b)(a-b) = a2-b2
- (x+a)(x+b) = x2+ x(a+b)+ab
- (a+b)3 = a3+3a2b+3ab2+b3
- (a-b)3 = a3-3a2b+3ab2-b3
- a3+b3 = (a+b)(a2-ab+b2)
- a3-b3 = (a-b)(a2+ab+b2)
- (a+b+c)2 = a2+b2+c2+2ab+2bc+2ca
Polynomial Equations
Polynomial Equations are the equations that are formed using polynomials. General form of polynomial equation is,
P(x) = anxn + … + a1x + a0
Examples of polynomial equations are,
- 3x3 + 5x2 – 4x – 11 = 0
- x2 + 2x + 1 = 0, etc.
Solving Polynomials
Solving polynomials or solving polynomial equations means finding the zeros or roots of the polynomial equation. There are various method to find the root of the polynomial equations.
Polynomial Functions
Polynomial functions are the function containing various polynomial, they have variables, coefficient, constant, etc. Example,
- f(x) = 2x2 – 4x + 1
- g(x) = x2 + x + 1
- h(x) = x3 + 2x2 + 3x + 4, etc.
Polynomial functions are very useful for presenting various types of curve and are used in all branches of Mathematics.
Read More,
Example 1: Find the degree of 5x5 – 2x3 + 4x2 – x + 4.
Solution:
Given Polynomial,
Highest exponent power in the polynomial is 5
Degree of polynomial is 5
Example 2: Add the polynomials 3x2 + 2x + 1 and 2x2 – 4x + 3.
Solution:
Given polynomials,
- 3x2 + 2x + 1
- 2x2 – 4x + 3
Adding these two polynomials,
= (3x2 + 2x + 1) + (2x2 – 4x + 3)
= (3x2 + 2x2) + (2x – 4x) + (1 + 3)
= 5x2 – 2x + 4
Example 3: Factorize x2 + 3x + 2
Solution:
= x2 + 3x + 2
= x2 + 2x + x + 2
= x(x + 2) +1(x + 2)
= (x + 1)(x + 2)
Example 4: Find the zeros of the polynomial 2x3 + 7x2 + 6x.
Solution:
= 2x3 + 7x2 + 3x
= x(2x2 + 7x + 3)
= x(2x2 + 6x + x + 3)
= x{2x(x +3) +1(x +3)}
= x(2x + 1)(x + 3)
Zeros of the given polynomial are,
2x + 1 = 0
x + 3 = 0
Question 1: Find the value of x in the polynomial equation 2x2 – 5x + 3 = 0.
Solution:
We can solve this quadratic equation using the quadratic formula:
x = (-b ± √(b2 – 4ac)) / 2a
where a = 2, b = -5, and c = 3.
Substituting the values:
x = (5 ± √(25 – 423)) / 2*2
x = (5 ± √(25 – 24)) / 4
x = (5 ± √1) / 4
So, the solutions are:
x = (5 + 1) / 4 = 6 / 4 = 3/2
and x = (5 – 1) / 4 = 4 / 4 = 1.
Question 2: Factorize the polynomial x2 – 4x + 4.
Solution:
We observe that the given polynomial is a perfect square trinomial.
It can be written as (x – 2)2.
So, the factored form is (x – 2)(x – 2) or (x – 2)2.
Question 3: Find all the roots of the polynomial equation x^3 – 6x^2 + 11x – 6 = 0.
Solution:
We can use synthetic division or polynomial long division to factorize the polynomial and find its roots.
After factorizing, we find that the roots are x = 1, x = 2, and x = 3.
Question 4: Given the polynomial 3x4 – 7x3 + 2x2 – 5x + 1, find its degree and leading coefficient.
Solution:
The degree of a polynomial is the highest power of the variable present. In this case, the degree is 4. The leading coefficient is the coefficient of the term with the highest power of the variable. Here, the leading coefficient is 3.
Question 5: Simplify the expression (2x2 – 3x + 1)(x2 + 4x – 2).
Solution:
We use the distributive property to expand the expression:
(2x2 – 3x + 1)(x2 + 4x – 2) = 2x2(x2+4x−2)−3x(x2+4x−2)+1(x2+4x−2)
= 2x4+8x3−4x2−3x3−12x2+6x+x2+4x−2
= 2x4 + 5x3 – 15x2 + 10x – 2
Download class 10 polynomials chapter PDF which is important for students to excel in the class.
Practice Problems on Polynomial
Q1. Find the roots of the polynomial equation 2x2 – 5x + 7
Q2. Simplify, (x3 + 8)/(x + 2)
Q3. Find the roots of polynomial equation, 2x3 – 2x = 0
Q4. Factorize: x3 – 2x2 + 4x – 11 = 0
FAQs of Polynomial
What is a Polynomial?
A polynomial is an expression that involves variables (usually represented by letters) raised to powers and combined using addition, subtraction, and multiplication. The variables can have coefficients (numbers multiplying the variables) attached to them.
What are Examples of Polynomial?
Some examples of polynomials are:
- 3x2 + 2x – 1,
- 4y3 – 5y + 2,
- 7a4 – 2b2, etc.
What is Zero of Polynomial?
Zeros of a polynomial is a the value of the polynomial substituting it in the polynomial results in Zero. Suppose we have a polynomial P(x) then zero of the polynomial is ‘a’ if P(a) is zero.
What is Coefficient of a Polynomial?
In a variable there are various terms and the coefficient of each term is called the coefficient of a polynomial. For example, in a polynomial x2 + 2x + 3
- Coefficient of x2 is 1
- Coefficient of 2x is 2
What is Leading Coefficient of a Polynomial?
The coefficient of the highest degree term in the polynomial is called the leading coefficient of a polynomial.
What are Monomials, Binomials and Trinomials?
- Monomials are the polynomial with only one term. Example: 3x2
- Binomials are the polynomial with two terms. Example: 3x2 + 2x
- Trinomials are the polynomial with three terms. Example: 3x2 + 2x + 1
What is Constant in a Polynomial?
The constant term in the polynomial is the term with no variables. Suppose in the example, 3x2 + 2x + 1. The constant term is 1.
What are Polynomial Equations?
Equations which contains plynomials are called the polynomial equations various examples of the polynomial equations are,
- 3x3 + 8x – 5 = 0
- x + y + z = 0
- 3x + y – 5 = 0, etc.
The number of polynomials with zeros as ‒2 and 5 is?
There is 1 polynomial with zeros as -2 and 5, which is x2−3x−10.
Share your thoughts in the comments
Please Login to comment...