Domain and Range are the input and output values of a Function. A function is defined as the relation between a set of inputs and their outputs, where the input can have only one output i.e. a domain can yield a particular range. It depicts a relationship between an independent variable and a dependent variable. A function is usually denoted by y = f(x), where x is the input. A function is a relation f from a set X to another set Y, where each element in X has exactly one output in Y, and it is represented as f: X→Y. Here the set X is known as the domain of a function, and the set Y is called the co-domain of the function. Every function has a domain, codomain, and range that help in defining the function.
In this article, we will learn about the domain and range of a function, how to calculate the domain and range of a function, domain and range of a function worksheet, domain and range of a function examples, domain and range of a function graph and others in detail.
What is Domain and Range?
The domain of a function is defined as the set of all possible values for which the function can be defined. Range is the output given by a function for a particular domain. A co-domain of a function is the set of possible outcomes, whereas a range or image of a function is a subset of a co-domain and is the set of images of the elements in the domain. For example, in the figure given below, f(x) = x3 is a function whose domain is the set X, and its co-domain is the set Y while its range is {1, 8, 27, 64}.
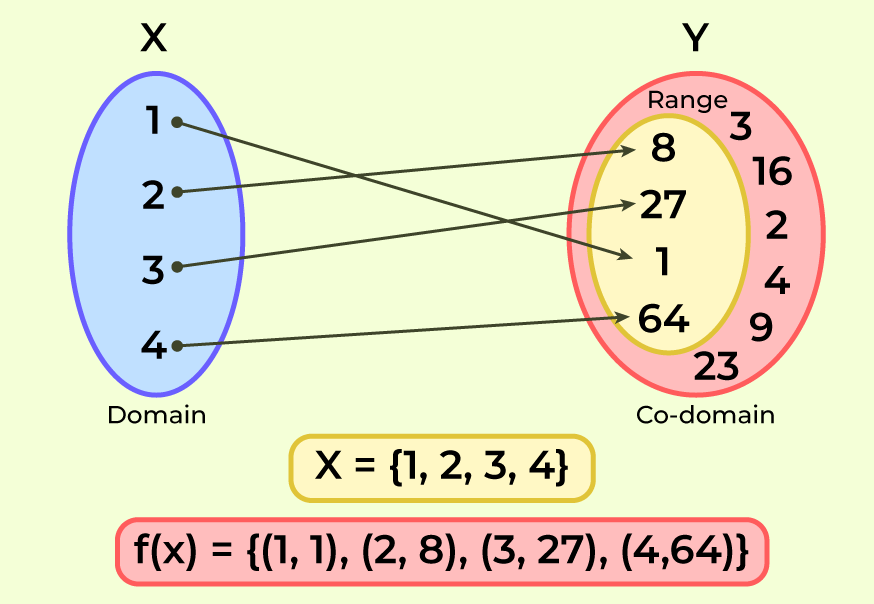
Domain of a Relation can also be found using the same methods. A relation is a type of function in which one object in the domain region is mapped to more than one object in the range region.
For the given function f(x) = x3
- f(x) = {(1,1), (2,8), (3,27), (4,64)}
- Domain = {1, 2, 3, 4}
- Co-domain = {1, 2, 3, 4, 8, 9, 16, 23, 27, 64}
- Range = {1, 8, 27, 64}
Interval Notation of Domain and Range
Domain and range of any function can be easily written in the Interval Notation. Suppose we are given any function f(x) = sin x then its domain and range is written as,
- Domain of f(x) = (-∞, +∞)
- Range of f(x) = [-1, 1]
Similarly using the interval notation we can represents the domain and range of any function.
How to Write Domain and Range
Domain and range of any function can be easily represented using the Interval Notation as shown above. In this way we use brackets to describe a set of numbers. We use {}, [], and () to represent the domain and range of the function.
Co-Domain and Range
Codomain is the set of the values including the range of the function nd it can have some additional values. Range is the Subset of the Codomain. This is explained using the example,
Given function, f(x) = cos x, such that, f:R→R, then
- Codomain of f(x) = R
- Range of R = (-1, 1)
Domain of a Function
The domain of a function is defined as the set of all possible values for which the function can be defined. Let us go through the domains of different functions.
- The domain of any polynomial function such as a linear function, quadratic function, cubic function, etc. is a set of all real numbers (R).
- The domain of a logarithmic function f(x) = log x is x > 0 or (0, ∞).
- The domain of a square root function f(x) = √x is the set of non-negative real numbers which is represented as [0, ∞).
- The domain of an exponential function is the set of all real numbers (R).
- A rational function is defined only for non-zero values of its denominator. So, to determine the domain of a rational function y = f(x), set the denominator ≠ 0.
Rules of Finding Domain of a Function
Various rules for finding the domain of the function.
- Domain of the Polynomial functions (linear, quadratic, cubic, etc) function is R (all real numbers).
- Domain of the square root function √x is x ≥ 0.
- Domain of the exponential function is R.
- Domain of the logarithmic function is x > 0.
- We know that, the domain of a rational function y = f(x), denominator ≠ 0.
How to Find the Domain of a Function?
To find the domain of a function, use the following steps:
Step 1: First, check whether the given function can include all real numbers.
Step 2: Then check whether the given function has a non-zero value in the denominator of the fraction and a non-negative real number under the denominator of the fraction.
Step 3: In some cases, the domain of a function is subjected to certain restrictions, i.e., these restrictions are the values where the given function cannot be defined. For example, the domain of a function f(x) = 2x + 1 is the set of all real numbers (R), but the domain of the function f(x) = 1/ (2x + 1) is the set of all real numbers except -1/2.
Step 4: Sometimes, the interval at which the function is defined is mentioned along with the function. For example, f (x) = 2x2 + 3, -5 < x < 5. Here, the input values of x are between -5 and 5. As a result, the domain of f(x) is (-5, 5).
After taking all the steps discussed above the set of numbers left with us is considered the domain of a function.
Example of Domain
Find the domain of f(x) = 1/(x2 – 1)
Solution:
Given,
Now, putting x = -1, 1 in f(x)
- f(-1) = 1/{(-1)2 – 1} = 1/0 = ∞
- f(1) = 1/{(1)2 – 1} = 1/0 = ∞
Thus, on -1 and 1 the function is f(x) is undefined and apart form that at all points the f(x) is defined. Thus, the domain of f(x) is R – {-1, 1}
Range of a Function
Range of a Function is the set of all the outputs of the function. For any function f: A→ B the sets of values in the B are the range of the function. if f: A→ B is a function such that f(x) = x2 and A is the set of all integers then the range of the function is the set of Range = {1, 4, 9, 16, ….}. We have to note that the range of the function is the subset of the Co-Domain of the function.
Rules of Finding Range of a Function
Rules for finding the range of a function are,
- For linear function the range is R.
- For quadratic function y = a(x – h)2 + k the range is:
- y ≥ k, if a > 0
- y ≤ k, if a < 0
- For the square root function, the range is y ≥ 0.
- For the exponential function, the range is y > 0.
- For the logarithmic function, the range is R.
How to Find the Range of a Function?
The range or image of a function is a subset of a co-domain and is the set of images of the elements in the domain.
To find the Range of a Function use the following steps
Let us consider a function y = f(x).
Step 1: Write the given function in its general representation form, i.e., y = f(x).
Step 2: Solve it for x and write the obtained function in the form of x = g(y).
Step 3: Now, the domain of the function x = g(y) will be the range of the function y = f(x).
Thus, the range of a function is calculated.
Example of Range
Find the range of the function f(x) = 1/ (4x − 3).
Solution:
Given,
Let the function be f(x) = y = 1/ (4x − 3)
y(4x − 3) = 1
4xy – 3y = 1
4xy = 1 + 3y
x = 4y / (1 + 3y)
Here, we observe that x is defined for all the values except of y for y = −1/3 as on y = -1/3, we get an undefined value of x.
So, the range of f(x) = 1/ (4x − 3) is (−∞, −1/3) U (1/3, ∞)
How to Calculate Domain and Range
Now to calculate the domain and range of any given function study the following example carefully:
For X = {1, 2, 3, 4, 5} and Y = {1, 2, 4, 5, …, 45, 46, 47, 48, 49, 50} and the function defined as f: X → Y, f(x) = x2 find the domain and range of the following function f(x)
Domain = All the input values = X
Range = {1, 4, 9, 16, 25} = A subset of Y
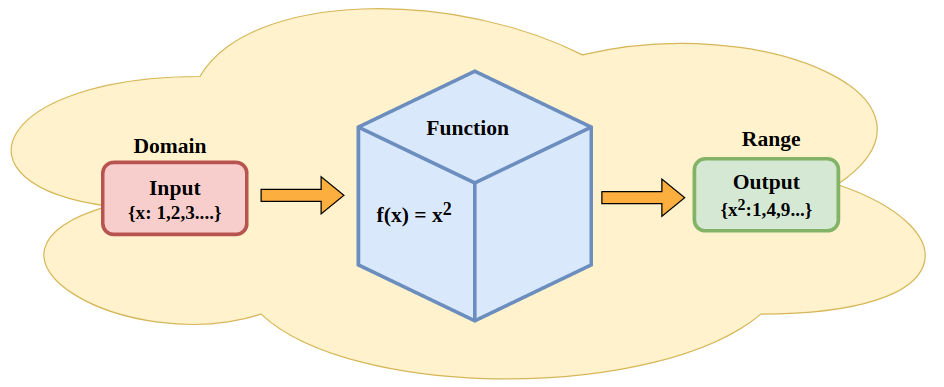
How To Calculate Domain And Range?
The domain of a function is the input value that we can take for a function and range of a function is the set of all the output values that the function achieves. Now domain and the range of the function is found using the example added below,
For example, if we are given a function F: X → Y, such that F(x) = y + 1, and X = {1, 2, 3, 4, 5} and Y = {1, 2, 3, 4, 5, 6}. Here,
- Domain of F(x) = X = {1, 2, 3, 4, 5}
- Range of F(x) = {2, 3, 4, 5, 6}
Y is the codomain of F(x) but not the range.
Domain and range of various types of functions are discussed in the next sections.
Domain and Range of a Function Examples
- Linear Functions: For [Tex]f(x)=2x+3[/Tex], the domain and range are all real numbers, since there are no restrictions on x and f(x).
- Quadratic Functions: For g(x)=[Tex]x^2−4[/Tex], the domain is all real numbers, but the range is [Tex]y≥−4[/Tex] because the output can’t be less than -4.
- Rational Functions: For ℎ(x)=[Tex]1/x-2[/Tex], the domain is x≠2 (all real numbers except 2), and the range is also all real numbers except where ℎ(x)=0.
Quadratic Domain and Range
A quadratic function is a polynomial function with degree 2, i.e. f(x): ax2 + bx = c = 0 is a Quadratic Function. And the Domain and range of a quadratic function is:
Domain of f(x): Set of Real Numbers = R
Range of f(x):
- y ≥ k, if a > 0, where k is any constant
- y ≤ k, if a < 0, where k is any constant
Domain and Range of Exponential Functions
The exponential function is defined as:
f: R → R, f(x) = ax
The domain of the exponential function is all the real numbers and as the exponential function always gives the positive output, the range is the set of all the positive real numbers.
Domain and Range of Trigonometric Functions
For trigonometric functions, the domain is a set of all real numbers (except some values in some functions) and the range of the trigonometric functions varies with different trigonometric functions, such that
- Range of Sine Function = [-1, 1]
- Range of Cosine Function = [-1, 1]
- Range of Cosecant Function = (−∞,−1]∪[1,+∞)
- Range of Secant Function = (−∞,−1]∪[1,+∞)
The range for Tangent and Cotangent functions is different,
- Range of Tangent Function = [-∞, ∞]
- Range of Cotangent Function = [-∞, ∞]
This can be summarized in the table below:
Trigonometric Functions
| Domain
| Range
|
|---|
| sin θ | R | [-1, 1] |
| cos θ | R | [-1, 1] |
| tan θ | R – (2n + 1)π/2 | R |
| sec θ | R – (2n + 1)π/2 | (−∞,−1]∪[1,+∞) |
| cosec θ | R – nπ | (−∞,−1]∪[1,+∞) |
| cot θ | R – nπ | R |
Domain and Range of an Absolute Value Function
Absolute functions also called modulus function are the functions that are defined for all real numbers but their output is only positive real numbers, an absolute function only gives a positive output.
An absolute function is defined as:
f: R → R, f(x) = |ax + b|
Thus, the Domain and Range of Absolute Value Function is:
Domain and Range of a Square Root Function
For a square root function, the domain and range are calculated as:
Suppose the square root function is, f(x) = √(ax + b)
We know that the square root of a negative number is not defined, so the domain of the square root function is,
- Domain = x ≥ -b/a = [-b/a,∞)
Now for the range of the square root function, we know that an absolute square root only gives positive values so the range is all positive real numbers.
Domain and Range of a Rational Function
A rational function is a function which is represented as, P(x)/Q(x) where P(x) and Q(x) are polynomial function and Q(x) is never zero. the domain of a rational function is the values of x for which Q(x) is never zero. And the range of the rational function are the values of y that are found using various values of x, in y = P(x)/Q(x).
Log Function Domain and Range
Log function or the Logarithmic function are the function of the form, y = ln x and the domain nd range of the log function is:
- Domain of Log function: (0, ∞)
- Range of Log function: (-∞, +∞)
Domain and Range of Greatest Integer Function
Greatest Integer Function is also called the step function and is the function that give the output as nearest integer less than or equal to the given number.
- Domain of Greatest Interger Funcion: R
- Range of Greatest Interger Funcion: Z
Domain and Range of a Function Graph
If the graph of any function is given then finding the domain and range is very easy task. Suppose we are given any curve then finding wether the curve is function or not is our first priority and this is found using the vertical line test. Then if the curve is given in the form y = f(x), then the projection on the graph on the x-axis gives the Domain of the function and the projection of the graph on the y-axis gives the range of the function.
Domain and Range of a Function Worksheet
- Consider the function f(x)=√(x−2). Determine the domain and range of this function.
- Given the function g(x)=1/(x+3), find its domain and range.
- For the function h(x)=(x2−4)/x−2, determine the domain and range.
- Explore the function k(x)=sin(x). What are the domain and range of this trigonometric function?
- Investigate the function m(x)=ex. Identify its domain and range.
Domain and Range Worksheet PDF
Download PDF of Domain and Range Worksheet which contains numerical questions.
Domain and Range Practice Problems
Practice problems on Domain and Range in statistics are provided below:
Domain and Range Quiz
1. What is the domain of the function f(x) = √(x − 41) ?
A) x ≥ 0
B) x > 41
C) x ≥ 41
D) x ≤ 41
2. Which of the following functions has a range of (−∞,0] ?
A) g(x) = 1/x
B) h(x) = √x
C) k(x) = sin(x)
D) m(x) = ex
3. What is the range of the function f(x) = 1/ (x+2) ?
A) y > 0
B) y ≤ 0
C) y ≠ 0
D) y ≠ −2
4. For which of the following functions is the domain all real numbers?
A) g(x) = 1/(x−3)
B) h(x) = x2−9
C) k(x) = ln(x+2)
D) m(x) = tan(x)
5. What is the domain of the function f(x) = log(x2+4) ?
A) x > 0
B) x ≥ 0
C) x ≠ 0
D) x ∈ R
Answers
- C) x ≥ 41
- B) h(x) = √x
- B) y ≤ 0
- A) g(x) = 1/(x−3)
- B) x ≥ 0
Solved Questions on Domain and Range
Question 1: Find the domain of a function f(x) = (2x + 1)/ (x2 − 4x + 3).
Solution:
Given Function.
f(x) = (2x + 1)/ (x2 − 4x + 3)
f(x) = (2x + 1)/ (x − 1)(x − 3)
Observing the function we can say that the function f(x) is defined for all the values of x except for the values where, the denominator of the function is zero.
So f(x) is not defined when,
(x − 1)(x − 3) = 0
This can be acheived if of the bracket is zero, i.e.
x − 1 = 0 => x = 1 is where the function f(X) is undefined.
x − 3 = 0 => x = 3 is where the function f(X) is undefined.
Thus, the domian of f(x) is all the values except {1, 3}
Domain of f(x) = R − {1, 3}
Hence, the domain of the given function f(x) is R − {1, 3}.
Question 2: Find the domain and range of a function f(x) = x2 + 1.
Solution:
Given Function,
f(x) = x2 + 1
This is a polynomial function and we know that a polynomial function is defined for all the values of x.
Thus, f(x) is defined for all x
Domain of f(x) = R = (-∞, ∞)
For Range,
Let f(x) = y = x2 + 1
y = x2 + 1
⇒ x2 = y − 1
⇒ x = √(y − 1)
The square root of the function is defined for all the vaues except for the negative values.
So, (y − 1) ≥ 0
y ≥ 1
Thus, the range of the function is, [1, ∞)
Question 3: Find the domain and range of a function f(x) = (x + 2)/ (x – 3).
Solution:
Given Function,
f(x) = (x + 2)/ (x – 3)
Observing the function we can say that the function f(x) is defined for all the values of x except for the values where, the denominator of the function is zero.
Thus the function is defined for all the values of x but not where x-3 = 0
x – 3 = 0
⇒ x = 3
So, the domain of f(x) is R-{3}
For Range,
Let y = f(x)
⇒ y = (x + 2)/ (x – 3)
⇒ y(x – 3) = (x + 2)
⇒ xy – 3y = x + 2
⇒ xy – x = 3y + 2
⇒ x (y – 1) = 3y + 2
⇒ x = (3y + 2)/ (y – 1)
Observing the above equation we can say that x is defined for all the values except for the values where the denominator of the functiuon is zero, i.e.
y – 1 = 0
⇒ y = 1
Range of f(x) = R – {1}
Question 4: Find the domain and range of a function f(x) = 3ex/7.
Solution:
Given Function,
f(x) = 3ex/7
It is an exponential function which is defined for all the values of x.
So, Domain of f(x) is R
For Range
Let f(x) = y
y = 3ex/7
⇒ ex = 7y/3
⇒ x = loge(7y/3)
We know that logarithmic functions are defined only for the positive values of x.
So, x is defined only when y > 0
Thus, range of f(x) is (0, ∞)
Domain and Range – FAQs
What are domain and range of a function?
Domain are the input values that a function takes and is defined and range of a function is the value for that domain
What is a function?
In mathematics, a function is defined as the relation between a set of inputs and their outputs, where the input can have only one output.
How is a function represented in Mathematics?
A function is a relation f from a set X to another set Y, where each element in X has exactly one output in Y, and it is represented as f: X→Y. A function is usually denoted by y = f(x), where x is the input.
What is the domain in Maths example?
The domain of a function is defined as the set of all possible values for which the function can be defined. The domain of any polynomial function such as a linear function, quadratic function, cubic function, etc. is a set of all real numbers (R).
What is the co-domain and range of a function?
A co-domain of a function is the set of possible outcomes, whereas a range or image of a function is a subset of a co-domain and is the set of images of the elements in the domain.
What are the domain and range?
The values that we input in a function are called the domain of the function and the range of the output value is called the range of the function.
How do you find the domain and range?
The domain of the function is found by taking the set of all the input value of the function and the range of the function is the set of all values that are in the output range of the function.
What are the domain and range of a set?
Domain of any function is the set of values that are allowed to use in place of independent variable and the range of the function are all the values of the independent variable.
Share your thoughts in the comments
Please Login to comment...