Dividing Polynomials as the name suggests the process of division of a polynomial by another polynomial. It is also called Polynomial Division. As we know, any expression with one variable with its various powers and coefficients is called a polynomial. The most general form of a polynomial is given as:
anxn + an−1xn−1 + … + a2x2 + a1x + a0
Where a0, a1, a2, . . ., an are the real coefficients. In Dividing Polynomial we divide the polynomial with a higher degree by a polynomial (that can monomial, binomial, trinomial, or any other higher degree polynomial) with less degree.
In this article, we will learn about all the necessary topics for the division of polynomials such as methods of division i.e., Long Division Method, Synthetic Division, etc. Also, we will learn how to solve problems related to Dividing Polynomials.
What is Dividing Polynomials or Division of Polynomials?
Dividing Polynomials in maths is an arithmetic operation in which one polynomial is divided by another polynomial, where the divisor polynomial must have a degree less than or equal to the Dividend Polynomial otherwise division of polynomial can’t take place.
There are various methods of Dividing Polynomials, some of those methods are:
- Long Division
- Synthetic Division
- Polynomial Division Using Factors
Long Division of Polynomials
The long division method is the most frequent and general method for dividing polynomials by binomials or any other form of polynomials. In case the given numerator and denominator do not have any common factors, you can simplify the expression by using the long division method.
How to Divide Polynomials Using Long Division
To divide the polynomial using Long Division, we can use the following steps:
Step 1: Arrenge both Divisors and Dividends in the decreasing order of degree of each of term i.e., anxn + an−1xn−1 + . . . + a1x + a0.
Step 2: Arrenge the Divisor and Dividend Long Division Form.
Step 3: Divide the the dividend’s first term(xn) by the divisor’s first term, and use it as the quotient’s first term.
Step 4: Multiply the divisor by the result of step 2 and arrenge them under the divident such that like terms aligned with each other.
Step 5: Subtract the result of step 3 from the divisor to create new polynomial.
Step 6: Repeat the steps 3, 4, 5 untill the resulting polynomial has a degree less then divisor.
Examples of Dividing Polynomials Using Long Division
Example: Divide x2 + 2x + 3 by x – 2.
Solution:
Step 1: Arrenge both Divisors and Dividends in the decreasing order of degree
Dividend = x2 + 2x + 3
Divisor = x – 2
Step 2: We will write the dividend and divisor in the long division form, like this:

Step 3: Divide the first term of the dividend by the first term of the divisor, to get the first term of divisor i.e.,
x2/x = x
This means that the first term of the quotient is x.
Step 4: Multiply the divisor (x – 2) by the first term of the quotient (x), and arrenge them under the divident with like terms aligned.

Step 5: Subtracted the result of step 3 from the dividend to get a new polynomial,

Step 6: We will repeat steps 3 and 4 using the new polynomial 4x + 3:
4x/x = 4
Multiplying divisor (x – 2) by the 4,

Step 7: Since the degree of the new polynomial 11, has a degree 0 which is less than the degree of the divisor (x – 2) i.e., 1, we can stop here.
So, the result of dividing the polynomial x2 + 2x + 3 by x – 2 is:
Quotient: x + 4 and Remainder: 11.
Example: Divide x3 + 2x2 – 5x + 1 by x – 2.
Solution:

Synthetic Division of Polynomials
It is a technique for dividing a polynomial by a linear binomial using only the coefficient values. We write the polynomials in standard form from the greatest degree term to the lowest degree term in this manner. Use zero as the coefficients of the missing terms when writing in descending powers.
How to Divide Polynomials Using Synthetic Division
To divide the polynomials using synthetic division, we can use the following steps:
Step 1: Write the polynomial in standard form, with the terms arranged in descending order of degree.
Let’s Suppose a polynomial as a3x3 + a2x2 + a1x + a0.
Step 2: Identify the divisor, and ensure that the divisor is in the form of x − k
Step 3: Write the value k to the left of the division symbol and place a vertical line to the right of it, and write the coefficients of the polynomial to be divided in the spaces to the right of the vertical line. Where any missing coefficients should be represented by zeros.

Step 4: Bring down the first coefficient and write it below the line, and multiple it with k and write the result in the next space to the right.

Step 5: Add both values in the second space and wrote it in space next to the leading coefficient.

Step 6: Multiply the result of Step 5 with k and write it in the third space, and add both column values to get the further result.

Step 7: Repeat this till reach the real constant part.

Step 8: The resulting values represent the coefficient of the remainder (last value) and qotient (other values).
Examples of Dividing Polynomials Using Synthetic Division
An example of the division of a polynomial using the synthetic division method of 3x4 + 5x + 9 by x – 1 is shown as follows:
Step 1: Write the polynomial in standard form, with the terms arranged in descending order of degree:
3x4 + 0x3 + 0x2 + 5x + 9
Step 2: Identify the divisor, and ensure that the divisor is in the form of x − k:
Divisor = x – 1
Step 3: Form the table of the given example,

Step 4: Bring down the first coefficient and write it below the line, and multiply it with k and write the result in the next space to the right:

Step 5: Add both values in the second space and write it in the space next to the leading coefficient:

Step 6: Multiply the result of Step 5 with k and write it in the third space, and add both column values to get the further result:

Step 7: Repeat this one more time,

Step 8: Repeat this one more time,

Step 9: The resulting values represent the coefficient of the remainder (last value) and quotient (other values).
Therefore, the quotient is 3x3 + 3x2+ 3x + 8 and the remainder is 11.
Example: Divide the polynomial x2 + x – 2 by x – 1 by synthetic division.
Solution:

The first two numbers of the last row represent the coefficients of the quotient and the third value is the remainder.
Thus, the quotient is x + 2 and remainder is 0.
Dividing Polynomial by Monomial
When a polynomial is divided by a monomial i.e., a polynomial with only one term in it, then the resulting polynomial can only be found if the degree of the divisor is less than or equal to the degree of the polynomial under consideration. We can divide a polynomial by a monomial using the following methods:
- Splitting the Terms Method
- Factorization Method
Let’s understand these methods in detail as follows:
Using Splitting the Term Method
This method involves splitting each term of the polynomial into separate terms and then simplifying them by dividing each term with the monomial. Let’s consider an example to understand this method better.
Example: Divide the polynomial 6x3 + 12x2 + 9x by the monomial 3x.
Solution:
Step 1: Split the polynomial into separate terms.
(6x3 + 12x2 + 9x) ÷ 3x = (6x3)/(3x) + (12x2)/(3x) + (9x)/(3x)
Step 2: Simplify each term by dividing with the monomial 3x:
(6x3 + 12x2 + 9x) ÷ 3x = 2x2 + 4x + 3
Therefore, 6x3 + 12x2 + 9x divided by 3x is equal to 2x2 + 4x + 3.
Using Factorization Method
This method involves factoring out the monomial from each term of the polynomial and then simplifying the expression. Let’s consider an example to understand this method better.
Example: Divide the polynomial 15x3 – 25x2 + 10x by the monomial 5x.
Solution:
Step 1: Factor out the monomial 5x from each term of the polynomial.
15x3 – 25x2 + 10x = 5x(3x2 – 5x + 2)
Step 2: The other factor than 5x is the required answer to the division.
5x(3x2 – 5x + 2)/5x = 3x2 – 5x + 2
Therefore, 15x3 – 25x2 + 10x divided by 5x is equal to 3x2 – x + 2.
Examples of Dividing Polynomial by Monomial
Let’s consider some more examples to further understand the concept of dividing a polynomial by a monomial.
Example 1: Divide the polynomial 2x2 + 6x + 4 by the monomial 2x.
Solution:
(2x2 + 6x + 4) ÷ 2x = (2x2)/(2x) + (6x)/(2x) + (4)/(2x)
(2x2 + 6x + 4) ÷ 2x = x + 3 + 2/x
Therefore, 2x2 + 6x + 4 divided by 2x is equal to x + 3 + 2/x.
Example 2: Divide the polynomial 9x3 – 15x2 + 6x by the monomial 3x.
Solution:
9x3 – 15x2 + 6x = 3x(3x2 – 5x + 2)
Therefore, 9x3 – 15x2 + 6x divided by 3x is equal to 3x2 – 5x + 2.
Dividing Polynomial by Binomial
Binomial is a polynomial that consists of two terms. There are two ways we can divide a polynomial by a binomial. If a binomial is the factor of the given polynomial, then we will factorize the polynomial and eliminate the common factor. However this is not the case always, in case there is no common factor between the binomial and the polynomial to be divided then we will using the Long Division Method.
Dividing Polynomial by Binomial using Factorization
Factorization is the method of writing the given polynomial into product of its factors. If the binomial by which we are dividing a given polynomial is the factor of the given polynomial then we can eliminate the binomial and we are left with the other factor as the quotient. This can be better understood by the example given below:
Example: Divide x2 + 4x + 3 by x + 1
Solution:
We have the Polynomial x2 + 4x + 3 as dividend
The binomial x + 1 is our divisior
We will factorize the polynomial x2 + 4x + 3 using Middle Term Splitting method
⇒ x2 + 4x + 3 = x2 + 3x + x + 3 = x2 + 3x + x + 3 = x(x + 3) + 1(x + 3) = (x + 1)(x + 3)
Now we can do the division as follows
(x2 + 4x + 3)/(x + 1) = (x + 1)(x + 3)/(x + 1)
Now we will eliminate the common part (x + 1).
Hence we are left with (x + 3) as the quotient.
Dividing Polynomial by Binomial using Long Division Method
Long Division Method is the conventional method of dividing polynomial when there is no common factor between the given polynomial and the binomial. This can be understood by following example
Example: Divide 2x2 + 7x – 3 by 2x + 1
Solution:
The process of dividing polynomial by a binomial using Long Division Method is explained in the image added below:

Common Mistakes to Avoid When Dividing Polynomials
There are some common mistakes done by students when dividing one polynomial by another. Some of these common mistakes are as follows:
- Making an error when performing the division: Double-check your arithmetic when performing the division. It is easy to make a mistake when working with long polynomials, so take your time and be thorough.
- Misaligning the terms when setting up the division: Make sure to align the terms correctly when setting up the division. Each term should be in the correct position relative to the other terms in the dividend and divisor.
- Forgetting to include the remainder: When dividing polynomials, there may be a remainder. Make sure to include the remainder in your answer, if there is one, and if the remainder is 0 then write 0 in the place of the remainder.
- Not simplifying the answer: Finally, simplify the answer as much as possible. This means combining like terms and putting the polynomial in standard form.
People Also Read:
Sample Problems on Dividing Polynomials
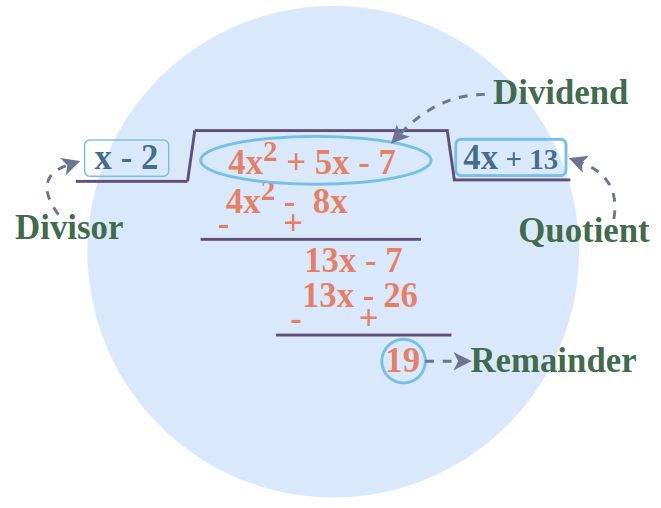
Problem 1. Using synthetic division, find the quotient and remainder of 
Solution:
Dividend = x2 + 3 or, x2 + 0x + 3
Divisor = x – 4
Applying synthetic division, we have:

The first two numbers of the last row represent the coefficients of the quotient and the third value is the remainder.
Thus, the quotient is x + 4 and the remainder is 19.
Problem 2. Solve  using long division.
using long division.
Solution:
Dividend = 4x3 + 5x2 + 5x + 8
Divisor = 4x + 1
Using long division method, we have:

Thus, the quotient and remainder are x2 + x + 1 and 7 respectively.
Problem 3. Solve  using synthetic division.
using synthetic division.
Solution:
Dividend = 4x3 – 3x2 + 3x – 1
Divisor = x – 1
Applying synthetic division, we have:

The first three numbers of the last row represent the coefficients of the quotient and the fourth value is the remainder.
The quotient is 4x2 + x + 4 and the remainder is 3.
Problem 4. Solve  using synthetic division.
using synthetic division.
Solution:
Dividend = 5x3 – 6x2 + 3x + 11
Divisor = x – 2
Applying synthetic division, we have:

The first three numbers of the last row represent the coefficients of the quotient and the fourth value is the remainder.
The quotient is 5x2 + 4x + 11 and the remainder is 33.
Problem 5. Solve  using long division.
using long division.
Solution:
Dividend = 18x4 + 9x3 + 3x2 + 0x + 0
Divisor = 3x2 + 1
Using long division method, we have:

Thus, the quotient and remainder are 6x2 + 3x – 1 and -3x + 1 respectively.
Dividing Polynomials Worksheet
1. Divide the polynomial x2 + 5x + 6 by x + 3
2. Use long division to divide 3x3 – 2x2 + 4x – 1 by x – 1
3. Divide 4x4 – 9x3 + 5x2 + x – 2 by 2x – 3.
4. Use long division to divide x4 + 2x3 – x + 4 by x2 – x + 1
5. Use synthetic division to divide 5x3 – 3x2 + 2x + 7 by x – 2.
FAQs on Dividing Polynomials
What is a Polynomial?
A polynomial is a mathematical expression that contains one or more terms involving variables raised to powers and coefficients. General polynomial of degree n is given by:
anxn + an−1xn−1 + … + a2x2 + a1x + a0
Where a0, a1, a2, . . ., an are the real coefficients.
What is Polynomial Division?
Polynomial division is a process of dividing a polynomial by another polynomial.
What is the Degree of a Polynomial?
The degree of a polynomial is the highest power of the variable in the polynomial.
What is Long Division of Polynomials?
Long division of polynomials is a method of dividing a polynomial by another polynomial,which is similar to long division of numbers.
What is Synthetic Division of Polynomials?
Synthetic division of polynomials is a shorthand method of polynomial division used when dividing a polynomial by a linear polynomial of the form (x – a), where a is a real constant.
What is Remainder Theorem?
In simple words, remainder theorem states that if a polynomial f(x) is divided by x – a, the remainder is equal to f(a).
What is Factor Theorem?
In simple words, factor theorem states that for a polynomial f(x) if f(a) = 0, then (x – a) is a factor of f(x).
How to know if One Polynomial is Divisible by Another?
One polynomial is divisible by another if the degree of the first polynomial is greater than or equal to the degree of the second polynomial, and if the second polynomial is a factor of the first polynomial.
Share your thoughts in the comments
Please Login to comment...