Vector Addition in Mathematics is the fundamental operation of vector algebra that is used to find the sum of two vectors. Vectors are mathematical quantities that have magnitude and direction. A vector can be represented by a line with an arrow pointing towards its direction and its length represents the magnitude of the vector.
Vector addition is achieved by taking the vector in 3D or 2D and then arranging them such that, the head of one vector is arranged touching the tail of the other vector and now a third vector joins the tail of the first vector with the head of the other vector gives the sum of the vectors.
In this article, we will learn about, vector definition, vector addition, laws of vector addition, and others in detail.
What is Vector?
Vectors are defined as,
“A quantity that has both magnitudes, as well as direction.”
It is denoted by an arrow pointing direction and length of its tail as the magnitude.
For any point P(x, y, z),
-
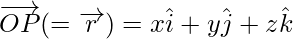
- Magnitude of vector r or
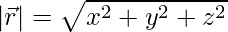
Vector Symbol
Vectors are represented using the symbols,  where A or |A| is the magnitude of the given vector.
where A or |A| is the magnitude of the given vector.
What is Vector Addition?
Vector addition is the operation in which two vectors are added to get their sum. Suppose we take two vectors, a and b, then that can be added together using vector addition, and the resultant vector is a + b.
Condition of Vector Addition
Various properties of vector addition are,
- We cannot add vectors and scalars together.
- Vectors can be added only if they are of the same nature. For instance, acceleration should be added with only acceleration and not mass.
- Vectors whose resultant have to be calculated behave independently.
- Vector Addition is nothing but finding the resultant of a number of vectors acting on a body.
- Vector Addition is commutative. This means that the resultant vector is independent of the order of vectors i.e.
 .
.
Consider two vectors P and Q, where,
- P = Pxi + Pyj + Pzk
- Q = Qxi + Qyj + Qzk
Then, the resultant vector is R = P + Q
R = (Px + Qx)i + (Py + Qy)j + (Pz + Qz) k
Vector Addition Properties Table
Various properties of the vector addition are added in the table below,
Vector Addition Properties
| Examples
|
|---|
Existence of Identity
| For any vector a,
a + 0 = a
Here, 0 vector represents additive identity.
|
Existence of Inverse
| For any vector a,
a + (-a) = 0
Here, (-a) vector represents additive identity.
|
Commutative Property
| For two vectors, a and b
a + b = b + a
|
Associative Property
| For three or more vector, a, b, and c
a + b + c = b + c + a
|
Vector Addition Calculator
You can use the following calculator to add any two vectors:
Laws of Vector Addition
There are three basic laws of vector addition that are used to add vectors and that include,
- Triangle Law of Vector Addition
- Parallelogram Law of Vector Addition
- Polygon Law of Vector Addition
Let’s understand these laws of vector addition in detail as follows:
Triangle Law of Vector Addition
If 2 vectors acting simultaneously on a body are represented both in magnitude and direction by 2 sides of a triangle taken in an order then the resultant(both magnitude and direction) of these vectors is given by 3rd side of that triangle taken in opposite order.
Read more about Triangle Law of Vector Addition.
Derivation of Triangle Law
Consider two vectors P and Q acting on a body and represented both in magnitude and direction by sides OA and AB respectively of a triangle OAB. Let θ be the angle between P and Q. Let R be the resultant of vectors P and Q. Then, according to the triangle law of vector addition, side OB represents the resultant of P and Q.

So, we have R = P + Q.
Now, expand A to C and draw BC perpendicular to OC.
From triangle OCB,
OB2=OC2 + BC2
⇒OB2 = (OA + AC)2 + BC2 . . . (i)
In triangle ACB,
cos θ = AC/AB
⇒ AC = AB cos θ = Q cos θ
Also, sin θ = BC/AB
⇒ BC = AB sin θ = Q sin θ
Magnitude of Resultant Vector
Substituting the value of AC and BC in (i), we get
R2 =(P + Q cos θ)2 + (Q sin θ)2
⇒R2 = P2 + 2 PQ cos θ + Q2 cos2 θ + Q2sin2 θ
⇒ R2 = P2 + 2PQ cos θ + Q2

Which is the magnitude of the resultant.
Direction of Resultant Vector
Let Φ be the angle made by resultant R with P. Then,
From triangle OBC,
tan Φ = BC/OC = BC/(OA + AC)
⇒ tan Φ = Q sin θ/(P + Q cos θ)
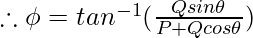
Which is the direction of the resultant.
Parallelogram Law of Vector Addition
If two vectors acting simultaneously at a point can be represented both in magnitude and direction by the adjacent sides of a parallelogram drawn from a point, then the resultant vector is represented both in magnitude and direction by the diagonal of the parallelogram passing through that point.
Note: In Euclidean geometry, it is necessary that the parallelogram should have equal opposite sides.
Derivation of Parallelogram Law
Let P and Q be two vectors acting simultaneously at a point and represented both in magnitude and direction by two adjacent sides OA and OD of a parallelogram OABD as shown in the figure.

Let θ be the angle between P and Q and R be the resultant vector. Then, according to the parallelogram law of vector addition, diagonal OB represents the resultant of P and Q.
So, we have R = P + Q.
Now, expand A to C and draw BC perpendicular to OC.
From triangle OCB,
OB2=OC2 + BC2
⇒OB2 = (OA + AC)2 + BC2 . . . (i)
In triangle ABC,
cos θ = AC/AB
⇒ AC = AB cos θ = OD cos θ = Q cos θ
[∵AB = OD = Q]
Also, sin θ = BC/AB
⇒ BC = AB sin θ = OD sin θ = Q sin θ
Magnitude of Resultant Vector
Substituting the value of AC and BC in (i), we get
R2 = (P + Q cos θ)2 + (Q sin θ)2
⇒R2 = P2 + 2 PQ cos θ + Q2 cos2 θ + Q2sin2 θ
⇒ R2 = P2 + 2PQ cos θ + Q2
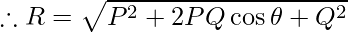
Which is the magnitude of the resultant.
Direction of Resultant Vector
Let ø be the angle made by the resultant R with P. Then,
tan Φ = BC/OC = BC/(OA + AC)
⇒ tan Φ = Q sin θ/(P + Q cos θ)
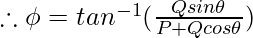
Which is the direction of the resultant.
Polygon Law of Vector Addition
Polygon law of vector addition states that,
“Resultant of a number of vectors can be obtained by representing them in magnitude and direction by the sides of a polygon taken in the same order, and then taking the closing side of the polygon in the opposite direction.”
In the specific case of vector A, vector B, vector C, and vector D, the results can be obtained by drawing a polygon with the vectors as its sides and then taking the closing side of the polygon in the opposite direction. The magnitude and direction of the resultant will be the same as the magnitude and direction of the closing side of the polygon.

On joining all vectors by connecting one’s tail with the other’s head, without changing their magnitude and direction we get a Polygon, and the vector joining the tail of the first and the head of the last vector is our Resultant vector ( ).
).

The formula for resultant of addition of two vectors 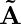 and
and  is:
is:
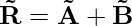
where,
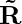 is the Resultant Vector
is the Resultant Vector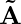 is the First Vector
is the First Vector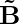 is the Second Vector
is the Second Vector
The general notation for the addition of vectors is:
If 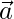 = <a1, a2, a3> and
= <a1, a2, a3> and 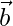 = <b1, b2, b3>, then their sum is given as:
= <b1, b2, b3>, then their sum is given as:
 = <a1 + b1, a2 + b2, a3 + b3>
= <a1 + b1, a2 + b2, a3 + b3>
Where,
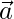 is the First Vector,
is the First Vector,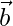 is the First Vector, and
is the First Vector, and - <a1 + b1, a2 + b2, a3 + b3> is the Resultant Vector.
Properties of Vector Addition
The vector addition is the sum of multiple (two or more) vectors. Two laws related to the addition of vectors are parallelogram law and triangle law. Similarly, the properties related to vector addition are:
- Closure property of addition: The sum of two vectors is also a vector. Hence, vectors are closed under addition.
- Associative Property
- Vector addition is commutative: It means that the order of vectors to be added together does not affect the result of the addition. If two vectors
 and
and  are to be added together, then
are to be added together, then 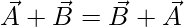
- Vector addition is Associative: While adding three or more vectors together, the mutual grouping of vectors does not affect the result. Mathematically,
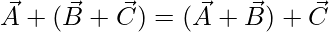
- Additive Identity: Zero vector (
 ) is the additive identity for a vector.
) is the additive identity for a vector. - Additive Inverse: The additive inverse of a
 is
is  i.e. often called the opposite vector of v; it has the same magnitude as the original and opposite direction.
i.e. often called the opposite vector of v; it has the same magnitude as the original and opposite direction. - Vector addition is Distributive: It means a scalar times the sum of two vectors is equal to the sum of the scalar times of the two vectors, individually. Mathematically,
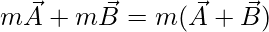
- The magnitude of the resultant of two vectors is less or equal to the sum of the magnitude of two vectors and greater or equal to the magnitude of the difference between the magnitude of two vectors.
Vector Subtraction
Vector subtraction of two vectors a and b is represented by a – b and it is nothing but adding the negative of vector b to the vector a. i.e., a – b = a + (-b).
Thus, the subtraction of vectors involves the addition of vectors and the negative of a vector. The result of vector subtraction is again a vector. The following are the rules for subtracting vectors:
- It should be performed between two vectors only (not between one vector and one scalar).
- Both vectors in the subtraction should represent the same physical quantity.
Vector Subtraction Formula
Here are multiple ways of subtracting vectors:
- To subtract two vectors a and b graphically (i.e., to find a – b), just make them coinitial first and then draw a vector from the tip of b to the tip of a.
- We can add –b (the negative of vector b which is obtained by multiplying b with -1) to a to perform the vector subtraction a – b. i.e., a – b = a + (-b).
- If the vectors are in the component form we can just subtract their respective components in the order of subtraction of vectors.
Thus, the addition formula can be applied as:

Note:  is nothing but
is nothing but  reversed in direction.
reversed in direction.
Properties of Vector Subtraction
There are various properties of vector subtraction, some of those properties are:
- Any vector subtracted from itself results in a zero vector. i.e., a – a = 0, for any vector a
- The subtraction of vectors is NOT commutative. i.e., a – b is not necessarily equal to b – a
- The vector subtraction is NOT associative. i.e., (a – b) – c does not need to be equal to a – (b – c)
- (a – b) · (a + b) = |a|2 – |b|2
- (a – b) · (a – b) = |a – b|2 = |a|2 + |b|2 – 2 a · b
Summary: Vector Addition
Following table summarizes the article in comprehensive manner:
Read More,
Examples of Addition of Vectors
Example 1: Two forces of magnitude 6N and 10N are inclined at an angle of 60° with each other. Calculate the magnitude of the resultant and the angle made by the resultant with 6N force.
Solution:
Let P and Q be two forces with magnitude 6N and 10N respectively and θ be angle between them. Let R be the resultant force.

So, P = 6N, Q = 10N and θ = 60°
We have,
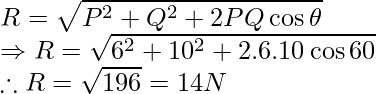
Which is the required magnitude.
Let ø be the angle between P and R. Then,
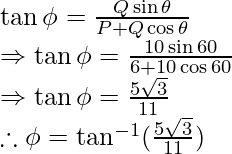
Which is the required angle.
Example 2: Find the addition of vectors PQ and QR, where PQ = (3, 4) and QR = (2, 6)
Solution:
We will perform the vector addition by adding their corresponding components
PQ + QR = (3, 4) + (2, 6)
⇒ PQ + QR = (3 + 2, 4 + 6)
⇒ PQ + QR = (5, 10).
Thus, the required answer is (5, 10).
Example 3: Two vectors are given along with their components: A = (2,3) and B = (2,-2). Calculate the magnitude and the angle of the sum C using their components.
Solution:
Let us represent the components of the given vectors as:
- In the A, Ax = 2 and Ay = 3
- In the B, Bx = 2 and By = -2
Now, adding the two vectors,
A + B = (2, 3) + (2, -2) = (4, 1)
It can also be written as:
C = (4, 1)
Here in C, Cx = 4 and Cy = 1
The magnitude of the resultant vector C can be calculated as:
|C| = √((Cx)2+(Cy)2)
⇒ |C| = √((4)2 + (1)2)
⇒ |C| = √(16 + 1)
⇒ |C| = √17 = 4.123 units (Approximately)
And the angle can be calculated as follows:
Φ = tan-1 (Cy/ Cx)
⇒ Φ = tan-1 (1/4)
⇒ Φ ≈ 14.04 degrees
Thus, the magnitude of the resultant vector |C| = 4.123 units (Approximately) and the angle Φ = 14.04 degrees
Example 4: If a = <1, -1> and b = <2, 1> then find the unit vector in the direction of addition of vectors a and b.
Solution:
The vector sum is:
a + b = <1, -1> + <2, 1> = <1 + 2, -1 + 1> = <3, 0>
Its magnitude is, |a + b| = √(32 + 02) = √9 = 3.
The unit vector in the direction of vector addition is:
(a + b) / |a + b| = <3, 0> / 3 = <1, 0>
Thus, the required unit vector is, <1, 0>.
Example 5: If a = <4, -2, 3> and b = <1, -2, 5> then find a – b.
Solution:
a – b = <4, -2, 3> – <1, -2, 5>
⇒ a – b = <4 – 1, -2 – (-2), 3 – 5>
⇒ a – b = <3, 0, -2>
Therefore, a – b = <3, 0, -2>.
Vector Addition-FAQs
What is Vector Addition in Mathematics?
Process of adding two vectors is known as vector addition, For example, there are two vectors a = <1, 2, 3> and b = < -1, -1, -1>, then their addition is, a + b = < 1 + (-1), 2 + (-1), 3 + (-1)> = < 0, 1, 2 >.
What is the formula for vector addition?
For vectors a = xi + yj + zk and b = pi + qj + rk, sum of a and b is given by c i.e.,
c = (xi + yj + zk) + (pi + qj + rk) = (x+p)i + (y+q)j + (z+r)k
What are the 2 methods of vector addition?
There are two methods of Vector Addition, that are:
- Triangle Law of Vector Addition
- Parallelogram Law of Vector Addition
What is Associative Property of Vector Addition?
The associative property of vector addition states that the sum of the vectors remains the same regardless of the order in which they are arranged.
Can the Sum of Two Vectors be Zero?
Yes, two vectors with equal magnitude and pointing in opposite directions will have the sum equal to zero.
How would you add two vectors?
To add two or more vectors we use various law of vector addition that are,
- Triangle Law of Vector Addition
- Parallelogram Law of Vector Addition
What is the rule for adding vectors?
Rule of Vector Addition are,
- Triangle Law of Vector Addition
- Parallelogram Law of Vector Addition
They are used to two or more vectors.
Share your thoughts in the comments
Please Login to comment...