Fractions have been used since ancient times by people to describe some part of the whole. Fractions are defined as part of the whole and it is widely used by common being without even thinking about them. The first ancient record of fractions was found in ancient Egypt, where Egyptians used fractions for portioning rations, livestock, and other things related to food and the kingdom. The word ‘Fraction’ is derived from the Latin word ‘Fractus’, which means ‘broken’ in English, and it fits right to the meaning of fraction. In this article, we will learn about fractions in detail including their types, operations no fractions, their properties, etc. Also the conversion between fractions and decimals and vice versa.
Table of Content
What is a Fraction?
If any object is divided in some number of equal parts and some of these parts are taken at once, then fraction is defined as the ratio of the number of taken parts to the total number of divided parts.
For example, a pizza is divided into 8 equal parts, and one part is taken out, thus the fraction representing the taken out part is 1/8 as one part is taken out of 8 equal parts. 1/8 part of the pizza can be represented in many forms such as:
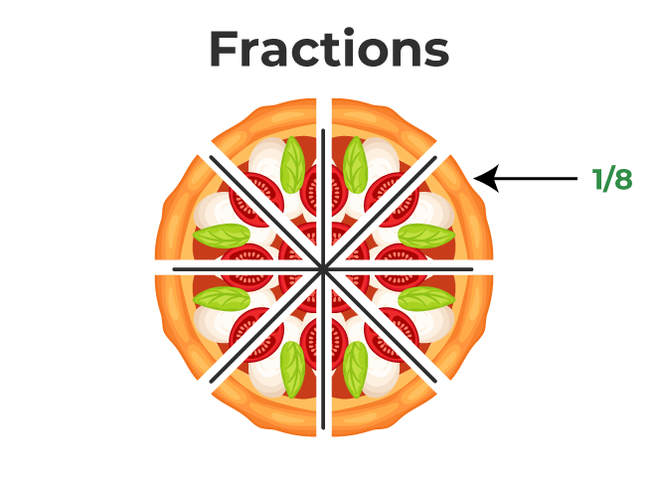
The remaining parts collectively will be 7/8 of the pizza as of now; there are only 7 pieces left. Similarly, if we take three parts of this pizza then the fraction representing the taken part will be 3/8 and if 2 pieces are taken out, they will be 2/8 of the entire pizza. It can be simplified and written as 1/4.
Parts of a Fraction
There are two parts to any fraction, numerator and denominator. The number at the top is known as the numerator and the bottom number is known as the denominator. If we divide anything into some equal parts then:
Numerator
The numerator represents how many parts of the whole are taken and it is the upper part of the fraction. For example, 3 is the numerator in 3/5, 4 is the numerator in 4/11, 13 is the numerator in 13/7, etc.
Denominator
The denominator represents the total number of equal parts of the whole and is the lower part of the fraction. For example, 5 is the denominator in 3/5, 11 is the denominator in 4/11, 7 is the denominator in 13/7, etc.
Properties of Fractions
There are some important properties of fractions similar to whole numbers, natural numbers, etc. Let’s take a look at those properties:
- For the Addition of fractions and multiplication of fractions, commutative and associative properties are true.
- Fractional multiplication gives 1, and the identity element is 0.
- The multiplicative inverse property reciprocates the fraction. That is, a/b is b/a, where a and b are non-zero numbers.
- The distributive property of multiplication over addition holds true for fractions.
Types of Fractions
There are majorly four types of fractions. They are unit fractions, proper fractions, improper fractions, and mixed fractions. They are categorized on the basis of their numerator and denominator. Let’s learn about all four types in detail:
Unit Fraction
A unit fraction is defined as a fraction with 1 as a numerator and is known as a Unit Fraction, for example – 1/8, 1/10, 1/4, 1/6, 1/11, etc. It can be said that all unit fractions are proper fractions since all unit fractions have 1 in the numerator, which is lesser than the denominator. The below-given example explains unit fractions very nicely. Here, a cake is divided into 4 equal parts. If the whole cake is 1, then each quarter of the cake is the fraction 1/4.
Proper Fraction
A Proper fraction is defined as a fraction in which the numerator value is less than the denominator value then. It is known as a proper fraction, for example, 4/9, 1/10, 2/5, 3/7, 5/9, etc.
Improper Fraction
An Improper fraction is defined as a fraction in which the numerator value is greater than the denominator value, then it is known as an improper fraction, for example, 6/5, 11/10, 11/5, 5/3, 2/1, etc.
Mixed Fraction
A Mixed fraction consists of a whole number with a proper fraction then, it is known as a mixed fraction. For Example, if 2 is a whole number and 1/4 is a fraction, then 2¼ is a mixed fraction.
Other Types of Fractions
Other types of fractions are on the basis of groups. They involve like and unlike fractions and equivalent fractions. All three types of fractions are explained below in complete detail.
Like Fractions
Any two or more fractions whose denominators are the same are known as like fractions. In other words, those fractions which can be added or subtracted together without taking the lcm of denominators are called like fractions. Some examples of like fractions are as follows:
- 2/9, 3/9, 5/9, 9/9, 4/9 (Here, the denominators of all the fractions are the same, that is, 9).
- 3/10, 7/10, 1/10, 9/10, 6/10 (Here, the denominators of all the fractions are the same, that is, 10).
- 1/7, 2/7, 4/7, 5/7, 7/7, 8/7.
- 1/2, 7/2, 6/2, 5/2, 9/2.
- 7/5, 1/5, 4/5, 3/5.
Unlike Fractions
The fractions whose denominators are different are called, unlike fractions. In other words, those fractions which can’t be added or subtracted together without taking the lcm of denominators are called, unlike fractions. Some examples of, unlike fractions are:
- 9/2, 1/6, 5/4, 7/3 (Here, the denominator of all the fractions is different).
- 1/2, 1/4, 2/3, 5/6, 8/9 (Here, the denominator of all the fractions is different).
- 3/8, 2/3, 3/5, 2/7.
- 1/9, 2/7, 3/4, 2/5, 3/2.
- 4/2, 1/6, 2/3, 7/5.
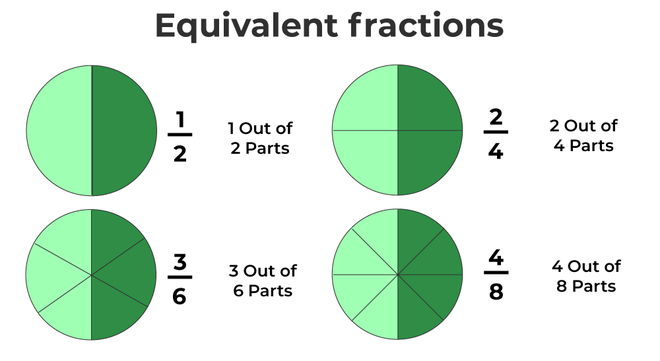
Equivalent Fractions
Equivalent fractions are defined as those fractions which result in the same value after simplification, and then they are equivalent to each other. Solving equivalent fractions can be done by either multiplying both the numerator and denominator by the same number or dividing the numerator and denominator by the same number. Below are some examples of equivalent fractions:
Example: Find two equivalent fractions of 4/12.
Solution:
Equivalent fraction by multiplying with the same number, lets multiply by 2:
(4 × 2)/(12 × 2) = 8/24
Equivalent fraction by division with the same number, here, both numerator and denominator are divisible by 4, dividing by 4:
(4 ÷ 4)/(12 ÷ 4) = 1/3
Operations on Fractions
Operations on fractions are simple arithmetic operations like addition, multiplication, division, etc. Let’s take a look at the operations that we can do on fractions:
Reduction of Fractions
Reducing fractions is simplifying fractions by dividing both the numerator and denominator with the same value. It is important to note that dividing them by 1 will not make any change in the fraction.
Example: Reduce the fraction 88/42
Solution:
88/42 is an improper fraction and both numerator and denominator are divisible by 2. Dividing them by 2:
88/42 = 44/21
Therefore, the reduced fraction becomes 44/21.
Multiplication of Fractions
Multiplication of fractions does not require any common denominator. Here, simply the numerator is multiplied by the numerator of the other fraction, and the denominator is multiplied by the denominator. It can also be simplified afterward if the fraction can be reduced. Fractions can also be simplified while multiplying with each other.
Example: How to multiply fractions, fractions 21/5 and 35/12.
Solution:
Multiplying fractions:
Addition of Fractions
Addition of fractions is possible only when the denominator is the same, in case the denominators of the fractions are not the same, it is important to bring them to a common denominator. Find the LCM of fractions in order to find the common denominator.
Example: How to add fractions 4/5 and 7/3.
Solution:
Here, the denominators of both fractions are not same, LCM of 3 and 5 is 15,
4/5 + 7/3 = (12 + 35)/15
= 47/15
Division of Fractions
Division of fractions does not require any common denominators. The simplest way to divide fractions is to flip the fraction after the division sign, that is, reciprocate the fraction, and change the sign from division to multiplication. Now, simply apply the multiplication of fractions rules and solve.
Example: How to divide fractions 35/20 and 5/10.
Solution:
Dividing fractions: 35/20 ÷ 7/10
Flipping the fraction after division sign and changing the sign to multiplication sign:
35/20 × 10/7
Reducing the fractions:
7/4 × 10/7 = 70/28 = 10/4 = 5/2
Therefore, the answer is 5/2.
Subtraction of Fractions
Subtraction of fractions is possible only when the denominator is the same. In case the denominators of the fractions are not the same, it is important to bring them to a common denominator. Find the LCM of fractions in order to find the common denominator.
Example: Subtract fractions 1/2 from 3/5.
Solution:
The least common denominator of 2 and 5 is 10. Solving:
1/2 – 3/5 = (5-6)/10
= -1/10
Fraction on a Number Line
Fractions on a number line are represented between the interval of two integers. Fractions are a part of the whole. Therefore, the whole is divided into equal parts, the number of parts between the integers is decided by the denominator value, and the numerator value is the point where the fraction lies. For example, if we are required to represent 1/8 on a number line, the division will be between 0 and 1, and since 8 is in the denominator, the whole is divided into 8 equal parts, where the first represents 1/8. Similarly, the second part represents 2/8, and so on.
How to Convert Fractions into Decimals?
Decimals are the numbers that represent fractions but in decimal form. For instance, 1/4 in fraction can be written as 0.25 in decimal form. Decimals are mostly preferred as they can be used for multiple mathematical operations where solving fractions seems complex, like addition, subtraction, etc. For example: In order to add 1/2 and 1/4, it is easier to solve the terms in decimals. Converting fractions into decimals ⇢ 0.5 + 0.25 = 0.75.
How to Convert a Decimal into a Fraction?
Decimals are converted into decimals as sometimes mathematical operations are easily solved in fraction form. Mathematical operations like multiplication and division are sometimes easier with fractions. Following are the steps that can be followed to convert a decimal into a fraction:
- Convert the decimal into p/q form where q = 1.
- Now multiply the numerator and denominator by 10 till the numerator becomes a whole number from decimals. For example, if there are two numbers after the decimal point, multiply and divide by 100.
- Now, simplify the fraction obtained.
Example: Convert 0.8 into a fraction.
Solution:
- Convert into p/q form ⇢ 0.8/1
- Multiply 10/10 ⇢ 0.8/1 × 10/10
- Simplifying fraction ⇢ 8/10 = 4/5.
Fractions to Percentage
After converting fractions into decimals, we can convert fractions into percentages as well. For converting Fractions into percentages steps that needed to be followed are as follows:
Step 1: Convert the fraction to a decimal by dividing the numerator by the denominator.
Step 2: Multiply the decimal by 100.
Step 3: Add the percent symbol (%).
Example: Convert 3/4 to a percentage.
Solution:
Step 1: 3 ÷ 4 = 0.75
Step 2: 0.75 × 100 = 75
Step 3: 75%
Therefore, 3/4 is equivalent to 75%.
Example: Convert 5/13 to a percentage.
Solution:
Step 1: Divide the numerator (5) by the denominator (13):
5 ÷ 13 = 0.38461538
Step 2: Multiply the result by 100 to convert it to a percentage:
0.38461538 × 100 = 38.461538 %
Step 3: Round the percentage to the desired number of decimal places, if necessary.
Therefore, 5/13 is equivalent to 38.46 % (rounded to 2 decimal places).
Value of Pi in Fraction
Pi (Ï€) is a mathematical constant that is defined as the ratio of a circle’s circumference to its diameter. The value of pi in decimal is approximately equal to 3.14. The value of pi (Ï€) in fractions is approximated to 22/7 which is the most popular approximation of Ï€. Other than 22/7, 355/113, 3 1/7, 104348/33215, etc. are also some lesser-known fractional approximations of Ï€. The value of pi is used both in decimal and fraction form based on the type of question given.
Also, read
Solved Examples on Fractions
Example 1: Write two equivalent fractions of 3/39.
Solution:
Equivalent fraction by multiplying with the same number, lets multiply by 2:
(3 × 2)/(39 × 2)
= 6/78
Equivalent fraction by division with the same number, here, both numerator and denominator are divisible by 3, dividing by 3:
(3 ÷ 3)/(39 ÷ 3)
= 1/13
Example 2: In a class of 90 students, 1/3rd of the students do not like cricket. How many students like cricket?
Solution:
Fraction of students that do not like cricket = 1/3
Fraction of student that like cricket = 1 – 1/3
= (3 – 1)/3
= 2/3rd students like cricket.
Number of students that like cricket = 2/3 × 90
= (2 × 30)
= 60
Therefore, 60 students like cricket.
Example 3: What type of fraction is this – 1/2, 1/5, 1/7, 1/10, 1/3?
Answer:
This is a Unit fraction because all the fractions have 1 as a numerator.
Example 4: If a recipe needs 3/4 cup of sugar and you want to make half the recipe, how much sugar do you need?
Answer:
Sugar needed for recipe = 3/4 cup
Suger needed for half the recipe = 1/2 of 3/4
Required sugar = 1/2 × 3/4 = 3/8
Therefore, we need 3/8 cup of sugar.
Example 5: What is the equivalent fraction of 7/5?
Answer:
To find the equivalent fraction of 7/5, we need to multiply both numerator and denominator by the same number.
Hence, (7/5) × (2/2) = 14/10
Therefore equivalent fraction of 7/5 is 14/10.
Example 6: John ran 5/6 of a mile on Monday and 7/8 of a mile on Tuesday. How many miles did he run in total?
Solution:
Total miles John ran in total is = 5/6 + 7/8
And the least common multiple of 6 and 8 is 24,
5/6 = 20/24,
and 7/8 = 21/24
5/6 + 7/8 = 20/24 + 21/24 = 41/24
Thus, John ran 41/24 miles in total.
Example 7: What fraction of a day is 8 hours?
Answer:
We know that 1 day has 24 hours.
1 hour = 1/24 days
8 hours = 1/24 × 8 days
8 hours = 8/24 = 1/3 days
Therefore, 8 hours has 1/3 days.
Example 8: A rectangle has a length of 3/4 meter and a width of 1/2 meter. What is the area of the rectangle?
Solution:
Area of Rectangle = Length of rectangle × Breadth of the rectangle
Given: Length = 3/4 meter and Breadth = 1/2 meter
Area = (3/4) × (1/2) = 3/8
Therefore, the area of the rectangle is 3/8 square meters.
Example 9: Ram drove 5/8 of the distance from his house to the store, and then drove another 1/4 of the distance. What is the remaining fraction of the distance he still has to drive?
Solution:
Let us assume the total distance be 1 unit.
Ram drove 5/8 of 1 = 5/8 unit and
again he drove 1/4 of 1 = 1/4 unit
Total distance covered till now = 1/4 + 5/ 8 = 7/8
Remaining distance = 1 – 7/8 = 1/8
Therefore,Ram has 1/8 of the distance left to drive.
Example 10: A school has 300 students, and 5/6 of the students take the bus to school. How many students don’t take the bus?
Solution:
Total number of student in school = 300 students
Students who take bus = 5/6 of the total students
⇒ Students who take bus = 5/6 × 300 = 250 students
Thus, students who don’t take the bus = 300 – 250 = 50 students
Therefore, 50 students don’t take the bus to school.
Example 11: A jar contains 1/3 red marbles, 1/4 blue marbles, and 5 green marbles. How many marbles in the jar?
Solution:
Let’s assume jar has x marble.
Red marbles = 1/3 × x = x/3
and Blue marbles = 1/4 × x = x/4
Thus, red marbles + blue marble = x/3 + x/4 = (3x+4x)/12 = 7x/12
So, 7x/12 of the marbles are red or blue.
Green marbles = x – 7x/12 = 5x/12
Given jar has 5 green marbles,
⇒ 5x/12 = 5
⇒ x = 12
Therefore, there are 12 marbles in the jar.
FAQs on Fractions
1. What are Fractions?
A fraction is the ratio of two natural number where first part of the ratio is called numerator and second part of the ratio is called denominator, and these two parts are seperated by a horizontal line.
2. What is a Proper Fraction?
A proper fraction is defined as a fraction in which the numerator valur is smaller than the denominator value. For example, 3/5, 5/7, 11/13, 9/17, etc.
3. What is an Improper Fraction?
An Improper fraction is defined as a fraction in which the numerator value is greater than the denominator value, then it is known as an improper fraction, for example, 7/5, 13/10, 9/5, 17/3, 5/1, etc.
4. What is a Mixed Fraction?
A mixed fraction is a combination of a whole number and proper fraction. For example, 2 1/2 (2 whole 1. by 2), 7 2/5 (7 whole 2/5), etc.
5. How to Compare Fractions?
We compare fractions is done to understand which fraction is larger or which fraction is smaller among the given fractions. If the denominator of the fractions given are same, only the numerators are compared, if the fractions have different denominators, first the LCM of fractions are taken and denomiantoras are made equal, and then the numerators are compared.
For example, 3/19 and 7/19 when compared, it can be observed that the denominator are same, therefore, numerators are compared, 3 > 7, therefore, 7/19 > 3/19.
6. How to Multiply Fractions?
Multiplication of fraction do not require any common denominator. Here, simply the numerator is multiplied by numerator of the other fraction and denominator is multiplied by the denominator. It can also be simplified afterwards if the fraction can be reduced. Fractions can also be simplified while multiplying with each other. For example: 3/7 × 1/2 = 3/14.
7. How to Divide Fractions?
Division of fractions do not require any common denominators, the simplest way to divide fractions is to flip the fraction after division sign, that is, reciprocate the fraction, and change the sign from division to multiplication. Now, simply apply the multiplication of fractions rules and solve. For example: 4/9 ÷ 2/3 = 4/9 × 3/2 = 2/3.
8. How to Add Fractions?
Adding fractions is possible only when the denominator are same, incase the denominators of the fractions are not same, it is important to bring them to a common denominator. Find the LCM of fractions in order to find the common denominator. For example: 3/4 + 1/2 = 3/4 + 2/4 = 5/4.