Number of substrings divisible by 6 in a string of integers
Last Updated :
13 Sep, 2023
Given a string consisting of integers 0 to 9. The task is to count the number of substrings which when convert into integer are divisible by 6. Substring does not contain leading zeroes. Examples:
Input : s = "606".
Output : 5
Substrings "6", "0", "6", "60", "606"
are divisible by 6.
Input : s = "4806".
Output : 5
"0", "6", "48", "480", "4806" are
substring which are divisible by 6.
Method 1: (Brute Force) The idea is to find all the substrings of the given string and check if substring is divisible by 6 or not.
Time Complexity: O(n2).
Method 2:(Dynamic Programming) As discussed in Check if a large number is divisible by 6 or not. A number is divisible by 6 if last digit is divisible by 2 and sum of digits is divisible by 3. The idea is to use Dynamic Programming, which enables us to compute answer quickly and efficiently by tracking previously computed answers and using these stored answer instead of recomputing values.
Let f(i, m) be the number of strings starting at index i and sum of their digits modulo 3 (so far) is m and number it represents is even. So, our answer would be 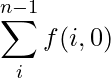
Let x be the ith digit in the string. From f(i, m) we need to find all the even substrings that start in i + 1. Also, we will get an extra substring if (x + m) itself is divisible by 3 and x is even. So, we get recurrence relation
// We initially pass m (sum modulo 3 so far) as 0
f(i, m) = ((x + m)%3 == 0 and x%2 == 0) +
f(i + 1, (m + x)%3) // Recursive
By memorizing the states, we get O(n) solution. Below is implementation of this approach:
C++
#include <bits/stdc++.h>
#define MAX 100002
using namespace std;
int f(int i, int m, char s[], int memoize[][3])
{
if (i == strlen(s))
return 0;
if (memoize[i][m] != -1)
return memoize[i][m];
int x = s[i] - '0';
int ans = ((x+m)%3 == 0 && x%2 == 0) +
f(i+1, (m+x)%3, s, memoize);
return memoize[i][m] = ans;
}
int countDivBy6(char s[])
{
int n = strlen(s);
int memoize[n+1][3];
memset(memoize, -1, sizeof memoize);
int ans = 0;
for (int i = 0; i < strlen(s); i++)
{
if (s[i] == '0')
ans++;
else
ans += f(i, 0, s, memoize);
}
return ans;
}
int main()
{
char s[] = "4806";
cout << countDivBy6(s) << endl;
return 0;
}
|
Java
import java.util.*;
class GFG
{
static int MAX = 100002;
static int f(int i, int m, char s[], int memoize[][])
{
if (i == s.length)
{
return 0;
}
if (memoize[i][m] != -1)
{
return memoize[i][m];
}
int x = s[i] - '0';
int ans = ((x + m) % 3 == 0 && x % 2 == 0) ? 1 + f(i + 1,
(m + x) % 3, s, memoize) : f(i + 1, (m + x) % 3, s, memoize);
memoize[i][m] = ans;
return memoize[i][m];
}
static int countDivBy6(char s[])
{
int n = s.length;
int[][] memoize = new int[n + 1][3];
for (int i = 0; i < n + 1; i++)
{
for (int j = 0; j < 3; j++)
{
memoize[i][j] = -1;
}
}
int ans = 0;
for (int i = 0; i < s.length; i++)
{
if (s[i] == '0')
{
ans++;
}
else
{
ans += f(i, 0, s, memoize);
}
}
return ans;
}
public static void main(String[] args)
{
char s[] = "4806".toCharArray();
System.out.println(countDivBy6(s));
}
}
|
Python3
def f(i, m, s, memoize):
if (i == len(s)):
return 0
if (memoize[i][m] != -1):
return memoize[i][m]
x = ord(s[i]) - ord('0')
ans = (((x + m) % 3 == 0 and x % 2 == 0) +
f(i + 1, (m + x) % 3, s, memoize))
memoize[i][m] = ans
return memoize[i][m]
def countDivBy6(s):
n = len(s)
memoize = [[-1] * 3 for i in range(n + 1)]
ans = 0
for i in range(len(s)):
if (s[i] == '0'):
ans += 1
else:
ans += f(i, 0, s, memoize)
return ans
if __name__ == '__main__':
s = "4806"
print(countDivBy6(s))
|
C#
using System;
class GFG
{
static int MAX = 100002;
static int f(int i, int m, char []s, int [,]memoize)
{
if (i == s.Length)
{
return 0;
}
if (memoize[i,m] != -1)
{
return memoize[i,m];
}
int x = s[i] - '0';
int ans = ((((x + m) % 3 == 0) && (x % 2 == 0)) ? 1 : 0)
+ f(i + 1, (m + x) % 3, s, memoize);
return memoize[i,m] = ans;
}
static int countDivBy6(char []s)
{
int n = s.Length;
int[,] memoize = new int[n + 1,3];
for (int i = 0; i < n + 1; i++)
{
for (int j = 0; j < 3; j++)
{
memoize[i,j] = -1;
}
}
int ans = 0;
for (int i = 0; i < s.Length; i++)
{
if (s[i] == '0')
{
ans++;
}
else
{
ans += f(i, 0, s, memoize);
}
}
return ans;
}
public static void Main(String[] args)
{
char []s = "4806".ToCharArray();
Console.WriteLine(countDivBy6(s));
}
}
|
Javascript
<script>
function f(i, m, s, memoize){
if (i == s.length)
return 0
if (memoize[i][m] != -1)
return memoize[i][m]
let x = s.charCodeAt(i) - '0'.charCodeAt(0)
ans = (((x + m) % 3 == 0 && x % 2 == 0) + f(i + 1, (m + x) % 3, s, memoize))
memoize[i][m] = ans
return memoize[i][m]
}
function countDivBy6(s){
let n = s.length
let memoize = new Array(n + 1)
for(let i=0;i<n + 1;i++){
memoize[i] = new Array(3).fill(-1)
}
let ans = 0
for(let i=0;i<s.length;i++){
if (s[i] == '0')
ans += 1
else
ans += f(i, 0, s, memoize)
}
return ans
}
let s = "4806"
document.write(countDivBy6(s))
</script>
|
Time Complexity: O(n).
Auxiliary Space: O(n)
Share your thoughts in the comments
Please Login to comment...