Last Minute Notes – Discrete Mathematics
Last Updated :
28 Jun, 2021
See Last Minute Notes on all subjects
here.
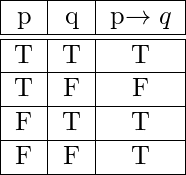
- Implication( →): For any two propositions p and q, the statement “if p then q” is called an implication and it is denoted by p → q.
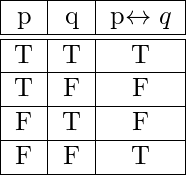
- if and only if(↔): For any two propositions p and q, the statement “p if and only if(iff) q” is called a biconditional and it is denoted by p ↔ q.
 De Morgan’s Law :
Special Conditional Statements
1.Implication :
De Morgan’s Law :
Special Conditional Statements
1.Implication : 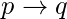 2.Converse : The converse of the proposition
2.Converse : The converse of the proposition 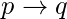 is
is 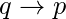 3.Contrapositive : The contrapositive of the proposition
3.Contrapositive : The contrapositive of the proposition 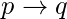 is
is 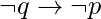 4.Inverse : The inverse of the proposition
4.Inverse : The inverse of the proposition 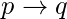 is
is 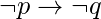 Types of propositions based on Truth values
1.Tautology – A proposition which is always true, is called a tautology.
2.Contradiction – A proposition which is always false, is called a contradiction.
3.Contingency – A proposition that is neither a tautology nor a contradiction is called a contingency.
There are two very important equivalences involving quantifiers
Types of propositions based on Truth values
1.Tautology – A proposition which is always true, is called a tautology.
2.Contradiction – A proposition which is always false, is called a contradiction.
3.Contingency – A proposition that is neither a tautology nor a contradiction is called a contingency.
There are two very important equivalences involving quantifiers
1.  2.
2. 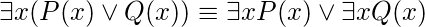
Rules of inference
![Rendered by QuickLaTeX.com \begin{tabular}{||c||c||c||} \hline Rule of Inference & Tautology & Name\\ \hline \rule{0pt}{8ex} \shortstack[l]{p \\ p\rightarrow q \\ \rule{1cm}{0.5pt}\\ \therefore q}& (p\wedge (p\rightarrow q)) \rightarrow q & Modus Ponens \\ \hline \rule{0pt}{8ex} \shortstack[l]{\neg q \\ p\rightarrow q \\ \rule{1cm}{0.5pt}\\ \therefore \neg p}& (\neg q \wedge (p\rightarrow q)) \rightarrow \neg p & Modus Tollens \\ \hline \rule{0pt}{8ex} \shortstack[l]{p\rightarrow q \\ q\rightarrow r \\ \rule{1.3cm}{0.5pt}\\ \therefore p \rightarrow r}& ((p\rightarrow q) \wedge (q\rightarrow r)) \rightarrow (p\rightarrow r) & Hypothetical syllogism \\ \hline \rule{0pt}{8ex} \shortstack[l]{ \neg p \\ p\vee q \\ \rule{0.8cm}{0.5pt}\\ \therefore q} & (\neg p \wedge (p\vee q)) \rightarrow q & Disjunctive Syllogism \\ \hline \rule{0pt}{8ex} \shortstack[l]{p \\ \rule{1.5cm}{0.5pt} \\ \therefore (p \vee q)}& p\rightarrow (p\vee q) & Addition \\ \hline \rule{0pt}{8ex} \shortstack[l]{ (p\wedge q)\rightarrow r \\ \rule{2.3cm}{0.5pt}\\ \therefore p\rightarrow (q\rightarrow r)} & ((p\wedge q)\rightarrow r) \rightarrow (p\rightarrow (q\rightarrow r)) & Exportation\\ \hline \rule{0pt}{8ex} \shortstack[l]{p\vee q\\\neg p\vee r \\ \rule{1.2cm}{0.5pt} \\ \therefore q\vee r}& ((p\vee q) \wedge(\neg p\vee r)) \rightarrow q\vee r & Resolution \\ \hline \end{tabular}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-29c02691ae71fa01c415b7cfe073d1b5_l3.png) Permutation: A permutation of a set of distinct objects is an ordered arrangement of these objects.
Permutation: A permutation of a set of distinct objects is an ordered arrangement of these objects.
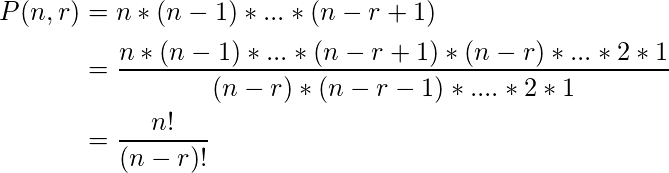
Combination: A combination of a set of distinct objects is just a count of the number of ways a specific number of elements can be selected from a set of a certain size. The order of elements does not matter in a combination.
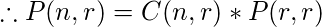 which gives us-
which gives us-
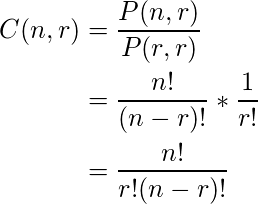
Binomial Coefficients: The 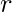 -combinations from a set of
-combinations from a set of 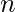 elements if denoted by
elements if denoted by  . This number is also called a binomial coefficient since it occurs as a coefficient in the expansion of powers of binomial expressions.
Let
. This number is also called a binomial coefficient since it occurs as a coefficient in the expansion of powers of binomial expressions.
Let 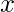 and
and  be variables and
be variables and 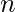 be a non-negative integer. Then
be a non-negative integer. Then
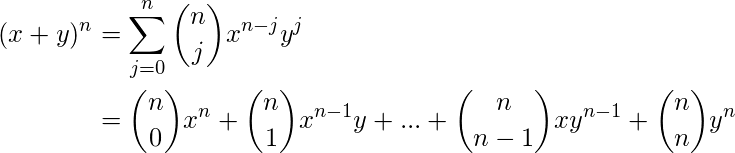
The binomial expansion using Combinatorial symbols
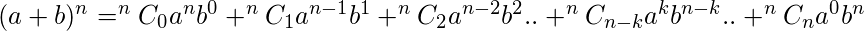
A Set is an unordered collection of objects, known as elements or members of the set.
An element ‘a’ belong to a set A can be written as ‘a ∈ A’, ‘a ∉ A’ denotes that a is not an element of the set A.
Equal sets
Two sets are said to be equal if both have same elements. For example A = {1, 3, 9, 7} and B = {3, 1, 7, 9} are equal sets.
NOTE: Order of elements of a set doesn’t matter.
Subset
A set A is said to be subset of another set B if and only if every element of set A is also a part of other set B.
Denoted by ‘⊆‘.
‘A ⊆ B ‘ denotes A is a subset of B.
To prove A is the subset of B, we need to simply show that if x belongs to A then x also belongs to B.
To prove A is not a subset of B, we need to find out one element which is part of set A but not belong to set B.
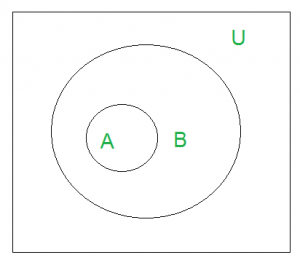 ‘U’ denotes the universal set. Above Venn Diagram shows that A is a subset of B.
Size of a Set
Size of a set can be finite or infinite.
For example
‘U’ denotes the universal set. Above Venn Diagram shows that A is a subset of B.
Size of a Set
Size of a set can be finite or infinite.
For example
Finite set: Set of natural numbers less than 100.
Infinite set: Set of real numbers.
Size of the set S is known as Cardinality number, denoted as |S|.
Note: Cardinality of a null set is 0.
Power Sets
The power set is the set all possible subset of the set S. Denoted by P(S).
Example: What is the power set of {0, 1, 2}?
Solution: All possible subsets
{∅}, {0}, {1}, {2}, {0, 1}, {0, 2}, {1, 2}, {0, 1, 2}.
Note: Empty set and set itself is also the member of this set of subsets.
Cardinality of power set is 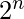 , where n is the number of elements in a set.
Cartesian Products
Let A and B be two sets. Cartesian product of A and B is denoted by A × B, is the set of all ordered pairs (a, b), where a belong to A and b belong to B.
, where n is the number of elements in a set.
Cartesian Products
Let A and B be two sets. Cartesian product of A and B is denoted by A × B, is the set of all ordered pairs (a, b), where a belong to A and b belong to B.
A × B = {(a, b) | a ∈ A ∧ b ∈ B}.
The cardinality of A × B is N*M, where N is the Cardinality of A and M is the cardinality of B.
Note: A × B is not the same as B × A.
Union
Union of the sets A and B, denoted by A ∪ B, is the set of distinct element belongs to set A or set B, or both.
Intersection
The intersection of the sets A and B, denoted by A ∩ B, is the set of elements belongs to both A and B i.e. set of the common element in A and B.
Disjoint
Two sets are said to be disjoint if their intersection is the empty set .i.e sets have no common elements.
Set Difference
Difference between sets is denoted by ‘A – B’, is the set containing elements of set A but not in B. i.e all elements of A except the element of B.
Complement
The complement of a set A, denoted by  , is the set of all the elements except A. Complement of the set A is U – A.
, is the set of all the elements except A. Complement of the set A is U – A.
Formula:
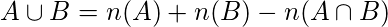
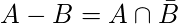
Group
A non-empty set G, (G, *) is called a group if it follows the following axiom:
- Closure:(a*b) belongs to G for all a, b ∈ G.
- Associativity: a*(b*c) = (a*b)*c ∀ a, b, c belongs to G.
- Identity Element:There exists e ∈ G such that a*e = e*a = a ∀ a ∈ G
- Inverses:∀ a ∈ G there exists a-1 ∈ G such that a*a-1 = a-1*a = e
|A| = m and |B| = n, then
1. No. of functions from A to B = nm
2. No. of one to one function = (n, P, m)
3. No. of onto function =nm – (n, C, 1)*(n-1)m + (n, C, 2)*(n-2)m …. +(-1)m*(n, C, n-1), if m >= n; 0 otherwise
4. Necessary condition for bijective function |A| = |B|
5. The no. of bijection function =n!
6. No. of relations =2mn
7. No. of reflexive relations =2n(n-1)
8. No. of symmetric relations = 2n(n+1)/2
9. No. of Anti Symmetric Relations = 2n*3n(n-1)/2
10. No. of asymmetric relations = 3n(n-1)/2
11. No. of irreflexive relations = 2n(n-1)
12. A relation is a partial order if
1) Reflexive
2) Antisymmetric
3) Transitive
13. Meet Semi Lattice :
For all a, b belongs to L a∧b exists
14. Join Semi Lattice
For all a, b belongs to L a∨b exists
15. A poset is called Lattice if it is both meet and join semi-lattice
16. Complemented Lattice : Every element has complement
17. Distributive Lattice : Every Element has zero or 1 complement .
18. Boolean Lattice: It should be both complemented and distributive. Every element has exactly one complement.
19. A relation is an equivalence if
1) Reflexive
2) symmetric
3) Transitive
1. No. of edges in a complete graph = n(n-1)/2
2. Bipartite Graph : There is no edges between any two vertices of same partition . In complete bipartite graph no. of edges =m*n
3. Sum of degree of all vertices is equal to twice the number of edges.
4. Maximum no. of connected components in graph with n vertices = n
5. Minimum number of connected components =
0 (null graph)
1 (not null graph)
6. Minimum no. of edges to have connected graph with n vertices = n-1
7. To guarantee that a graph with n vertices is connected, minimum no. of edges required = {(n-1)*(n-2)/2 } + 1
8. A graph is euler graph if it there exists atmost 2 vertices of odd – degree
9. Tree
-> Has exactly one path btw any two vertices
-> not contain cycle
-> connected
-> no. of edges = n -1
10. For complete graph the no . of spanning tree possible = nn-2
11. For simple connected planar graph
- A graph is planar if and only if it does not contain a subdivision of K5 and K3, 3 as a subgraph.
- Let G be a connected planar graph, and let n, m and f denote, respectively, the numbers of vertices, edges, and faces in a plane drawing of G. Then n – m + f = 2.
- Let G be a connected planar simple graph with n vertices and m edges, and no triangles. Then m ≤ 2n – 4.
- Let G be a connected planar simple graph with n vertices, where n ? 3 and m edges. Then m ≤ 3n – 6.