Welcome to the world of competitive programming, where we’ll explore the ABCs of Combinatorics – a fancy term for counting and arranging things. Think of it like solving puzzles with numbers and patterns. In this article, we’re diving into the Basics of Combinatorics that every competitive programmer needs to know. We’ll learn how to count, arrange, and select things in clever ways. These skills are like secret weapons for solving problems quickly and efficiently. So, get ready to boost your problem-solving game with the magic of Combinatorics!
What is Combinatorics?
Combinatorics is a branch of mathematics that focuses on counting, arranging, and analyzing discrete objects and structures. It deals with the study of different ways to select, arrange, and combine elements from finite sets or sequences, often in the context of discrete and finite structures. Combinatorics encompasses a wide range of topic.
Basic Rules of Combinatorics:
1. The Sum Rule:
If we have A number of ways of doing Task1 and B number of ways of doing Task2 then the total number of ways to choose one of the Task is equals to A+B.
So generally, if there are N tasks and i’th task can be done in a[i] ways then there are a1+ a2+ a3+… an ways to do one of the tasks.
Example:
Imagine you have 3 different Hats, 2 different shirts and 4 different pants. If you want to donate any one of the item what are the total number of ways to do say?
Answer: 3 + 2 + 4 = 9
2. The Product Rule:
If we have A number of ways of doing Task1 and B number of ways of doing Task2 then the total number of ways of doing both the tasks is equal to A*B.
So generally, if there are N tasks and i’th task can be done in a[i] ways then there are a1* a2* a3*… an ways to do all the task.
Example: Imagine you have 3 different Hats, 2 different shirts and 4 different pants. You want to get dressed and for that you have to wear 1 hat, 1 shirt and 1 pant. In how many ways you can do so?
Solution: 3 * 2 * 4 = 24
Fundamental Concepts in Combinatorics
Here, we’r going to introduce you to several fundamental concepts in combinatorics that is very useful:
The main use of factorial is counting the number of permutations (number of ways of arranging some objects). It can be used to answer following types of questions:
- Question 1. A class has just 3 seats vacant. Three people P, A, and R arrive at the same time. In how many ways can P, A, and R be arranged on those 3 vacant seats?
- Question 2. Find the number of ways of arranging 5 people if 2 of them always sit together?
- Question 3. Find all the three-letter words beginning and ending with a vowel. Given that repetition of alphabets is not allowed.
- click here to view how to use factorial in order to solve.
In permutation, we primarily deal with four kinds of problems.
A. Permutation with repetition:
Question: How many 3-digit numbers greater than 500 can be formed using 3, 4, 5, and 7?
Solution: Since a three-digit number, greater than 500 will have either 5 or 7 at its hundredth place, we have 2 choices for this place. There is no restriction on repetition of the digits, hence for the remaining 2 digits we have 4 choices each. So the total permutations are: 2 × 4 × 4 = 32
B. Permutation without repetition:
Question: How many 3-digit numbers divisible by 3 can be formed using digits 2, 4, 6, and 8 without repetition?
Solution: For a number to be divisible by 3, the sum of it digits must be divisible by 3
From the given set, various arrangements like 444 can be formed but since repetition isn’t allowed we won’t be considering them.
We are left with just 2 cases i.e. 2, 4, 6 and 4, 6, 8
The number of arrangements are 3! in each case
Hence the total number of permutations are: 3! + 3! = 12
C. r – permutation without repetition:
This is when we arrange just r objects out of n objects without repetition.
Question: An ice-cream shop has 10 flavors of ice cream. Find the number of ways of preparing an ice cream cone with any 3 different flavors?
Solution: Let us consider n = 10 (total number of flavors) and r = 3 (number of different flavors needed)
For first flavor we have 10 choices
For second flavor we have 10 – 1 choices
For third flavor we have 10 – 2 choices and this is same as (n – r + 1)
The numbers of arrangement would be: 10 × (10 – 1) × (10 – 3 + 1) = 720
From this we can generalize that, the number of ways of arranging r objects out of n different objects is:
n × (n – 1) . . . (n – r + 1) = nPr
D. r- permutation with repetition:
This can be thought of as the distribution of n objects into r boxes where the repetition of objects is allowed, and any box can hold any number of objects.
Question: A police officer visits the crime scene 3 times a week for investigation. Find the number of ways to schedule his visit if there is no restriction on the number of visits per day?
Solution: The number of ways to schedule first visit is 7 (any of the 7 days)
The number of ways to schedule second visit is 7 (any of the 7 days)
The number of ways to schedule third visit is 7 (any of the 7 days)
Hence, the number of ways to schedule first and second and third visit is 7 × 7 × 7 = 73 = 343
A combination of a set of distinct objects is just a count of the number of ways a specific number of elements can be selected from a set of a certain size. The order of elements does not matter in a combination.
An unordered selection of r elements from a set is called an r-combination. It is represented as C(n,r)
Since a combination is just a permutation without order, the number of r-combination can be expressed in terms of r-permutation.
The r-permutation can be obtained by first obtaining the r-combination and then ordering the elements in each r-combination, which can be done in P(r, r) ways.

which gives us:

Question: From a class of 30 students, 4 are to be chosen for the competition. In how many ways can they be chosen?
Solution: Total students = n = 30
Number of students to be chosen = r = 4
Hence, Total number of ways 4 students out of 30 can be chosen is,
30C4 = (30 × 29 × 28)/ (4 × 3 × 2 × 1)
= 24360/ 24
= 1015 ways
Question: Given two integers n and m, your task is to calculate the number of arrays such that below 4 conditions are satisfied:
- Size of array must be n
- All array element must be from 1 to m;
- For each array, there is exactly one pair of duplicate elements
- For each array there exists an i such that array is strictly increasing before i’th index and strictly decreasing after the i’th element.
Example: n=3, m=4
Output: 6
Explanation: [1,2,1], [1,3,1], [1,4,1], [2,3,2], [2,4,2], [3,4,3] are the arrays that satisfy the conditions.
Solution using combinatorics: Using condition 1 and 3, there will be exactly n-1 distinct elements in the array which is equal to 
Now we should have exactly one element that appears twice and we can choose from n-1 elements, but we cannot choose the maximum element because it will contradict our 4th condition. So, multiply our answer by (n-2)
finally, some elements will appear earlier than the maximum in our array, and some — later. The duplicated element will appear on both sides, but all other elements should appear either to the left or to the right, so there are  ways to choose their positions.
ways to choose their positions.
Thus, the final answer is 
A binomial coefficient C(n, k) can be defined as the coefficient of x^k in the expansion of (1 + x)^n. A binomial coefficient C(n, k) also gives the number of ways, disregarding order, that k objects can be chosen from among n objects more formally, the number of k-element subsets (or k-combinations) of a n-element set.
Formally, let x and y be variables and n be a non-negative integer. Then

Sometimes the required calculation may seem difficult to formulate, but using inclusion-exclusion with combinatorics we can calculate the required solution by Excluding the non-required solution from the total number of solutions. Let’s understand this with example:
Example 1: Count of permutations of numbers [0,9] such that first element is greater than 1 and last element is smaller than 8.
Solution using Inclusion Exclusion: We can revert the problem using the principle such that instead of calculating the original problem we can do the following:
- Count of permutations of numbers [0,9] such that first element is smaller than equal to 1 and last element is greater than equal to 8
- Subtract the Count of Step 1, from the total number of permutations possible.
Let X= set of permutations in which the first element is <=1 : 2*9 !
Let Y= set of permutations in which the last element is >=8 : 2*9!
Then 
Then by Inclusion Exclusion Principle:
 = 2*9! + 2*9! – 2*2*8!
= 2*9! + 2*9! – 2*2*8!
Subtract this count from the total number of permutations i.e. 10! to get the answer of the problem.
Example 2: Count how many subsequences of length ‘N’ exists consisting of only characters ‘a’, ‘b’ and ‘c’ such that each character occurs at least once.
Solution using Inclusion Exclusion: Again, we can change the framing of question such that we can calculate the count of such subsequences where ‘a’, ‘b’ and ‘c’ does not occur at all and subtract this count from the total number of the subsequences possible (3^n)
Let A = number of subsequences where ‘a’ does not occur
Let B = number of subsequences where ‘b’ does not occur
Let C = number of subsequences where ‘c’ does not occur
Then using Inclusion-Exclusion Principle:

which can be simplified to, 
Subtract this count from total number of subsequence possible i.e 3^n to get the answer.
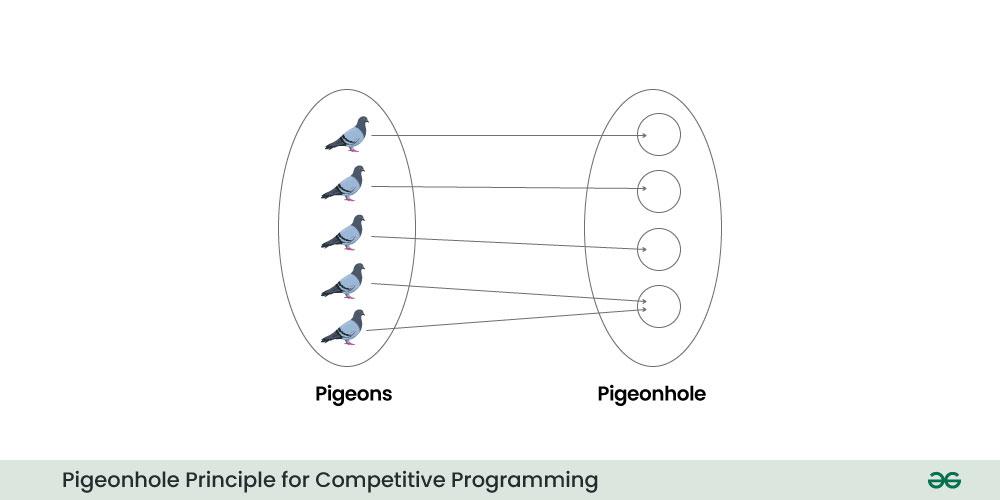
If you have more pigeons than pigeonholes into which you want to distribute those pigeons, at least one pigeonhole must contain more than one pigeon.
In other words, if you have n objects and m containers, where n > m, then at least one of the m containers must contain more than one object. This principle is named after the analogy of pigeons (objects) being placed in pigeonholes (containers).
Practice Problems on Combinatorics:
Related articles:
Share your thoughts in the comments
Please Login to comment...