Pigeonhole Principle for CP | Identification, Approach & Problems

In competitive programming, where people solve tough problems with computer code, the Pigeonhole Principle is like a secret tool. Even though it’s a simple idea, it helps programmers tackle complex challenges. This article is your guide to understanding how this principle works and why it’s crucial for competitive programmers. Let’s explore this powerful tool that turns ordinary coders into problem-solving wizards!

What is the Pigeonhole Principle?

If you have more pigeons than pigeonholes into which you want to distribute those pigeons, at least one pigeonhole must contain more than one pigeon.

In other words, if you have n objects and m containers, where n > m, then at least one of the m containers must contain more than one object. This principle is named after the analogy of pigeons (objects) being placed in pigeonholes (containers).

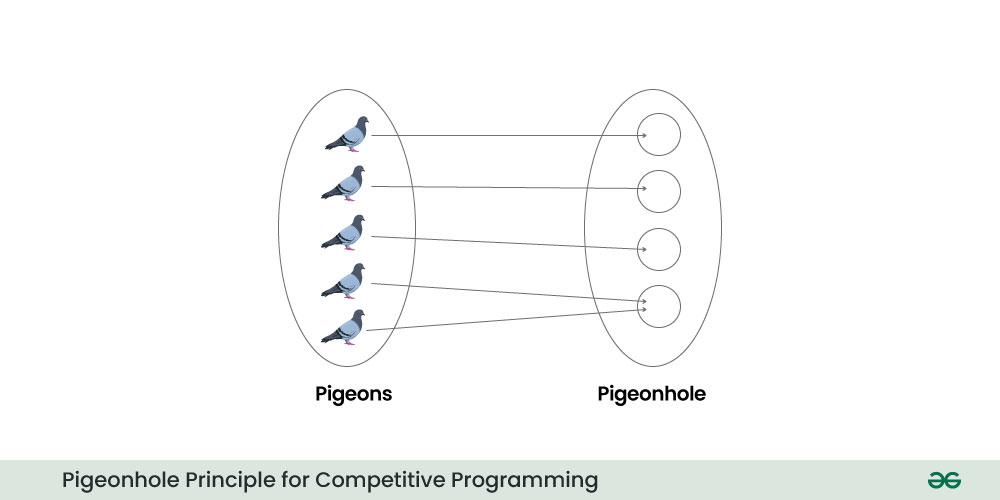
Pigeonhole Principle for Competitive Programming

Key Points of Pigeonhole Principle:

• It provides a simple way to prove the existence of certain arrangements or occurrences without explicitly finding them.
• It’s often used to establish the existence of duplicates, repetitions, or patterns within a set of objects or elements.
• The principle is a useful tool in various areas of mathematics, computer science, and problem-solving, including combinatorics, graph theory, and competitive programming.

How to Identify Pigeonhole Principle Problems ?

1. Observe the problem statement carefully: First, read the problem description carefully. Look for keywords that may indicate the presence of the Pigeonhole Principle, such as “divisible”, “distribution,” “buckets,” “categories,” “objects,” or “elements.”
2. Determine the distribution requirement: Distribution is a common indicator of the pigeonhole problem. Any problem requiring to distribution of elements(pigeons) into buckets (pigeonhole) may involve the pigeonhole principle.
3. Analyze Constraints: Analyze the constraints of the task, including the number of objects and classes (or pigeons). If the number of objects exceeds the number of categories(pigeonholes) , this is a strong indication that the Pigeonhole Principle can be applied.
4. Look for Repetitions: The pigeonhole principle often deals with patterns, repetitions, or duplicates between objects or elements.
5. Compare with known pigeonhole problems: If you have solved or encountered similar problems related to the Dovecote principle, please compare them. Some famous pigeon problems include:
   Birthday Paradox: In a group of 23, there is an even greater chance that at least two people have the same birthday. This intuitive result is an application of the pigeon principle.
   Socks in drawers: If the dresser has more socks than drawers, at least one drawer should have more than one sock.

Lets discuss some problems that will help you to get a idea about Pigeonhole Principle:

Problem 1:

Suppose there are n pairs of socks in the drawer, picking n+1 socks guarantees that at least one pair is chosen.

The Pigeonhole Principle is applied as follows:

Pigeons: In this case the individual socks we will have to pick will be the pigeons in this case.

Pigeonholes: A pair of socks consists of two socks of the same color, will be the pigeonholes in this case, There will be total n pigeonholes.

Marking the Pigeonholes and Applying Pigeonhole Principle: Now we pick n+1 socks. In the worst-case we will pick one sock from each pair . This means we will select n different socks, one from each pair, and they will go into separate pigeonholes. Thus, all pigeonholes will be marked.

Now when we pick (n+1)th sock, we will have to put it in one of existing pigeonholes which is already marked, thus the (n+1)th sock must necessarily match one of the previously chosen socks.

So, by applying the pigeonhole principle, we can conclude that picking n+1 socks from n pairs guarantees that at least one pair of socks is chosen.

Problem 2:

Suppose m and n are relatively prime positive integers, and 0 ≤ a < m and 0 ≤ b < n. We want to show that there exists an integer x such that x mod m = a and x mod n = b.

The Pigeonhole Principle is applied as follows:

Pigeons: Consider the integers a, a + m, a + 2m, …, a + (n – 1)m, each of these integers gives remainder a when divided by m. Let r₀ = a mod n, r₁ = (a+m) mod n, r₂ = (a+2*m) mod n , ……. , r_n-1 = (a+(n-1)*m) mod n be the remainders when the above integers are divided by m. We want to prove that one of these remainders will be equal will give equal to b, which will solve our problem. The above n remainders will be our pigeons in this case.

Pigeonholes: Let us proof the statement by contradiction. Consider n-1 boxes with number 0,1,2,3,…,b−1,b+1,…n−1. This will be the pigeonholes in this case. We will put the above remainder r_i into these boxes. We have not consider box b because we will try to show no such x exists

Applying Pigeonhole Principle: Since there are n remainders (pigeons) and n-1 boxes (pigeonholes), one box will contain two remainders. Let those two remainders be r_i and r_j , thus r_i=r_j

=> r_i = a + i*m – q1*n, and

=> r_j = a + j*m – q2*n

Since r_i=r_j ,

=> a + i*m – q1*n = a + j*m – q2*n

=> (j-i)* m= (q2- q1)*n,

This means that n divides (j-i).

But since i and j are distinct there values lie in {0,1,2,…,n−1}, 
=> 0 < (j – i) < n, this leads to a contradiction because n cannot divide a positive integer smaller than itself. Therefore, n does not divide (j – i).

Hence, two remainders cannot belong to same box. So one the of remainder will have to belong to box b, which implies one of the remainders r₀ , r₁ , ……. , r_n-1 will be equal to b.

Problem 3:

Given an array of n integers, where n is a positive integer. the task is to determine whether there exists a non-empty subset of the given array whose sum is divisible by n.

The Pigeonhole Principle is applied as follows:

Pigeons: The prefix sums of the array are calculated, and for each prefix sum, the remainder when divided by n is computed. These remainders are the “pigeons” in our problem.

Pigeonholes: The “pigeonholes” correspond to the distinct remainders that can occur when dividing by n (i.e., 0 to n-1).

Marking the Pigeonholes: An array remainderExists is used to mark which “pigeonhole” (remainder) are occupied. While iterating through the array of prefix sum if remainder of current prefix has already been marked in remainderExists, then answer will be yes.

The answer is always “YES” to this problem because of the Pigeonhole Principle. The number of distinct remainders when dividing any integer by n ranges from 0 to n-1, creating n possible “pigeonholes.” In contrast, when you calculate the prefix sums of an array, you start with a sum of 0, and you have n additional remainders (from 0 to n-1) in the prefix sum array. This means you have n+1 “pigeons” to place into the n “pigeonholes.”

By the Pigeonhole Principle, if you have more “pigeons” than “pigeonholes,” at least one “pigeonhole” must contain more than one “pigeon.” Therefore, there must exists a index in prefix sum array such that remainder(prefixsum[i]%n) has already been marked in remainderExists array. Therefore, there must be a subset of the array whose sum is divisible by n.

How to solve problems of Pigeonhole Principle?

1. Determine the Pigeons and Pigeonholes:

After Identifying the problem statement carefully, you need to determine the pigeons and pigeonholes in the problem. Pigeons are the objects which need to be distributed and pigeonhole corresponds to buckets into which pigeons will be distributed. As in the above-solved problem, the remainders were the pigeons in the problem and the pigeonholes corresponded to the distinct remainders that can occur when dividing by n.

2. Apply the Pigeonhole Principle:

Once the pigeons and pigeonholes have been identified, the pigeonhole principle can be applied. The Pigeonhole Principle states that if you have more pigeons than pigeonholes, then at least one pigeonhole must have more than one pigeon. Apply this to your problem by figuring out if there are more holes than holes. If your problem setup matches this, it means you can apply the pigeonhole principle.

Practice Problems of Pigeonhole Principle:

Find a non empty subset in an array of N integers such that sum of elements of subset is divisible by N
Maximum adjacent difference in an array in its sorted form
Construct String with given frequency and minimum continuous occurrence of a letter
Find a triplet (X, Y, Z) such that all are divisible by A, exactly one is divisible by both A and B, and X + Y = Z
Find Binary String of size at most 3N containing at least 2 given strings of size 2N as subsequences
Minimum number of socks required to picked to have at least K pairs of the same color
Count of subarrays of size K having at least one pair with absolute difference divisible by K-1
Largest subset with sum of every pair as prime