How to find the ratio in which a point divides a line?

Geo means Earth and metry means measurement. Geometry is a branch of mathematics that deals with distance, shapes, sizes, relevant positions of a figure in space, angles, and other aspects of a figure. Geometry can further be 2D or 3D geometry. 2D geometry deals with two-dimensional figures such as planes, lines, points, squares, polygons, etc. while 3D geometry is mainly concerned with three-dimensional figures or solid figures such as cubes, spheres, cuboids, etc. Let’s understand what a line segment is,

Line Segment 

Line Segment is characterized by two points in space. A line segment is a line joining two distinct points in space. The distance between these 2 points is known as the length of the line segment that connects these 2 points.

Properties of a line segment

• A line segment has a definite length,
• A line segment cannot be extended in any direction.
• A line segment has infinite points lying on it.
• A line segment has a fixed name say AB, QR, etc. This name denotes the 2 points that are the end points of the line segment.

In geometry, we generally encounter problems where we are supposed to find the ratio in which a point divides a line segment. In this article, we shall discuss this concept along with an example. Consider the line segment AB as shown in the following figure. Point O lies on the line segment and divides it into 2 parts.

Let the coordinates of points A, B, and O be (x₁, y₁), (x₂, y₂) and (x, y) respectively. We are supposed to find the ratio in which the Point O divides line segment AB. Let the ratio be k : 1. To calculate the ratio we proceed using the section formula which is as follows,

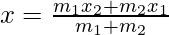 and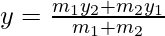 

Here, m₁ = k, m₂ = 1. Using these values in the above formula we get,

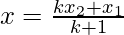 ⇢ (1)

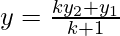⇢ (2)

Use any of the equations (1) or (2) to calculate the required ratio i.e. k. Let us look at an example.

Sample Problems

Question 1: Calculate the ratio in which line segment joining the points P(1, 8) and Q(4, 2) is divided by O(3, 4).

Solution:

The line segment joining P and Q is as shown below:

Given x₁ = 1, y₁ = 8, x₂ = 4, y₂ = 2, x = 3, y = 4. Let the ratio be k : 1.

Using section formula,

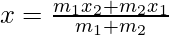
Putting the values in this formula we get:

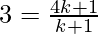
Solving for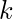 

3(k+1) = 4k+1

3k+3 = 4k+1

k = 2

Therefore, the point O divides the line segment PQ in ratio 2 : 1.

Question 2: Find the ratio in which the line segment joining the points A (-3, 3) and B (-2, 7) is divided by point O(1.5, 0).

Solution:

Given x₁ = 3, y₁ = 3, x₂ = -2, y₂ = 7, x = 1.5, y = 0

Let the required ratio be k : 1

Using Section Formula,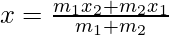 

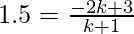
Solving for k, we get

1.5k+1.5 = -2k+3

3.5k = 2.5

k = 25/35 = 5/7

Therefore, the required ratio is 5:7

Question 3: Find the ratio in which the line segment joining A(1,−5) and B(−4,5) is divided by the x-axis.

Solution:

The point on the x-axis will be of the form (x, 0). Let the ratio be k:1

Given x₁ = 1, y₁ = -5, x₂ = -4, y₂ = 5, x = ?, y = 0

Using Section Formula,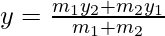 

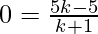
0 = 5k-5

k = 1

Therefore, the required ratio is 1:1

Question 4: If a point O(x, y) divides a line segment joining A(1, 5) and B(4, 8) in two equal parts. Find point O.

Solution:

Given x₁ = 1, y₁ = 5, x₂ = 4, y₂ = 8

We are given that the line is divided into 2 equal parts by the point O. Thus the ratio is 1:1.

Now using section formula,

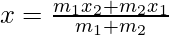
x= (4+1)/(1+1) = 5/2 = 2.5

Also,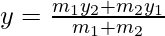 

y = (8+5)/(1+1) = 13/2

Therefore, the coordinates of the point O are (2.5, 6.5)