Introduction to Graph Coloring
Last Updated :
02 Apr, 2024
Graph coloring refers to the problem of coloring vertices of a graph in such a way that no two adjacent vertices have the same color. This is also called the vertex coloring problem. If coloring is done using at most m colors, it is called m-coloring.

Chromatic Number:
The minimum number of colors needed to color a graph is called its chromatic number. For example, the following can be colored a minimum of 2 colors.
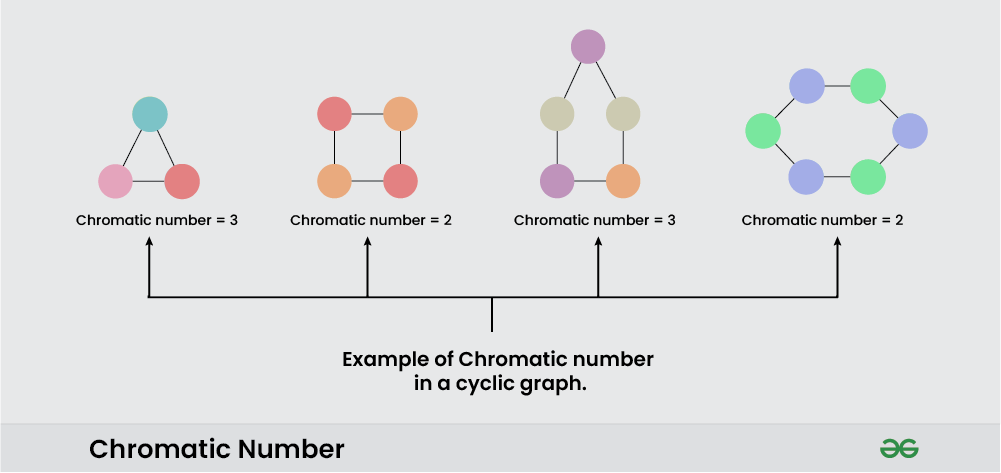
Example of Chromatic Number
The problem of finding a chromatic number of a given graph is NP-complete.
Graph coloring problem is both, a decision problem as well as an optimization problem.
- A decision problem is stated as, “With given M colors and graph G, whether a such color scheme is possible or not?”.
- The optimization problem is stated as, “Given M colors and graph G, find the minimum number of colors required for graph coloring.”
Algorithm of Graph Coloring using Backtracking:
Assign colors one by one to different vertices, starting from vertex 0. Before assigning a color, check if the adjacent vertices have the same color or not. If there is any color assignment that does not violate the conditions, mark the color assignment as part of the solution. If no assignment of color is possible then backtrack and return false.
Follow the given steps to solve the problem:
- Create a recursive function that takes the graph, current index, number of vertices, and color array.
- If the current index is equal to the number of vertices. Print the color configuration in the color array.
- Assign a color to a vertex from the range (1 to m).
- For every assigned color, check if the configuration is safe, (i.e. check if the adjacent vertices do not have the same color) and recursively call the function with the next index and number of vertices else return false
- If any recursive function returns true then break the loop and return true
- If no recursive function returns true then return false
Below is the implementation of the above approach:
C++
// C++ program for solution of M
// Coloring problem using backtracking
#include <bits/stdc++.h>
using namespace std;
// Number of vertices in the graph
#define V 4
void printSolution(int color[]);
/* A utility function to check if
the current color assignment
is safe for vertex v i.e. checks
whether the edge exists or not
(i.e, graph[v][i]==1). If exist
then checks whether the color to
be filled in the new vertex(c is
sent in the parameter) is already
used by its adjacent
vertices(i-->adj vertices) or
not (i.e, color[i]==c) */
bool isSafe(int v, bool graph[V][V], int color[], int c)
{
for (int i = 0; i < V; i++)
if (graph[v][i] && c == color[i])
return false;
return true;
}
/* A recursive utility function
to solve m coloring problem */
bool graphColoringUtil(bool graph[V][V], int m, int color[],
int v)
{
/* base case: If all vertices are
assigned a color then return true */
if (v == V)
return true;
/* Consider this vertex v and
try different colors */
for (int c = 1; c <= m; c++) {
/* Check if assignment of color
c to v is fine*/
if (isSafe(v, graph, color, c)) {
color[v] = c;
/* recur to assign colors to
rest of the vertices */
if (graphColoringUtil(graph, m, color, v + 1)
== true)
return true;
/* If assigning color c doesn't
lead to a solution then remove it */
color[v] = 0;
}
}
/* If no color can be assigned to
this vertex then return false */
return false;
}
/* This function solves the m Coloring
problem using Backtracking. It mainly
uses graphColoringUtil() to solve the
problem. It returns false if the m
colors cannot be assigned, otherwise
return true and prints assignments of
colors to all vertices. Please note
that there may be more than one solutions,
this function prints one of the
feasible solutions.*/
bool graphColoring(bool graph[V][V], int m)
{
// Initialize all color values as 0.
// This initialization is needed
// correct functioning of isSafe()
int color[V];
for (int i = 0; i < V; i++)
color[i] = 0;
// Call graphColoringUtil() for vertex 0
if (graphColoringUtil(graph, m, color, 0) == false) {
cout << "Solution does not exist";
return false;
}
// Print the solution
printSolution(color);
return true;
}
/* A utility function to print solution */
void printSolution(int color[])
{
cout << "Solution Exists:"
<< " Following are the assigned colors"
<< "\n";
for (int i = 0; i < V; i++)
cout << " " << color[i] << " ";
cout << "\n";
}
// Driver code
int main()
{
/* Create following graph and test
whether it is 3 colorable
(3)---(2)
| / |
| / |
| / |
(0)---(1)
*/
bool graph[V][V] = {
{ 0, 1, 1, 1 },
{ 1, 0, 1, 0 },
{ 1, 1, 0, 1 },
{ 1, 0, 1, 0 },
};
// Number of colors
int m = 3;
// Function call
graphColoring(graph, m);
return 0;
}
// Nikunj Sonigara
public class Main {
static final int V = 4;
// A utility function to check if the current color assignment is safe for vertex v
static boolean isSafe(int v, boolean[][] graph, int[] color, int c) {
for (int i = 0; i < V; i++)
if (graph[v][i] && c == color[i])
return false;
return true;
}
// A recursive utility function to solve m coloring problem
static boolean graphColoringUtil(boolean[][] graph, int m, int[] color, int v) {
if (v == V)
return true;
for (int c = 1; c <= m; c++) {
if (isSafe(v, graph, color, c)) {
color[v] = c;
if (graphColoringUtil(graph, m, color, v + 1))
return true;
color[v] = 0;
}
}
return false;
}
// This function solves the m Coloring problem using Backtracking.
// It returns false if the m colors cannot be assigned, otherwise, return true
// and prints assignments of colors to all vertices.
static boolean graphColoring(boolean[][] graph, int m) {
int[] color = new int[V];
for (int i = 0; i < V; i++)
color[i] = 0;
if (!graphColoringUtil(graph, m, color, 0)) {
System.out.println("Solution does not exist");
return false;
}
// Print the solution
printSolution(color);
return true;
}
// A utility function to print the solution
static void printSolution(int[] color) {
System.out.print("Solution Exists: Following are the assigned colors\n");
for (int i = 0; i < V; i++)
System.out.print(" " + color[i] + " ");
System.out.println();
}
// Driver code
public static void main(String[] args) {
// Create following graph and test whether it is 3 colorable
// (3)---(2)
// | / |
// | / |
// | / |
// (0)---(1)
boolean[][] graph = {
{ false, true, true, true },
{ true, false, true, false },
{ true, true, false, true },
{ true, false, true, false }
};
// Number of colors
int m = 3;
// Function call
graphColoring(graph, m);
}
}
V = 4
def print_solution(color):
print("Solution Exists: Following are the assigned colors")
print(" ".join(map(str, color)))
def is_safe(v, graph, color, c):
# Check if the color 'c' is safe for the vertex 'v'
for i in range(V):
if graph[v][i] and c == color[i]:
return False
return True
def graph_coloring_util(graph, m, color, v):
# Base case: If all vertices are assigned a color, return true
if v == V:
return True
# Try different colors for the current vertex 'v'
for c in range(1, m + 1):
# Check if assignment of color 'c' to 'v' is fine
if is_safe(v, graph, color, c):
color[v] = c
# Recur to assign colors to the rest of the vertices
if graph_coloring_util(graph, m, color, v + 1):
return True
# If assigning color 'c' doesn't lead to a solution, remove it
color[v] = 0
# If no color can be assigned to this vertex, return false
return False
def graph_coloring(graph, m):
color = [0] * V
# Call graph_coloring_util() for vertex 0
if not graph_coloring_util(graph, m, color, 0):
print("Solution does not exist")
return False
# Print the solution
print_solution(color)
return True
# Driver code
if __name__ == "__main__":
graph = [
[0, 1, 1, 1],
[1, 0, 1, 0],
[1, 1, 0, 1],
[1, 0, 1, 0],
]
m = 3
# Function call
graph_coloring(graph, m)
#This code is contrubting by Raja Ramakrishna
using System;
class GraphColoringProblem
{
// Number of vertices in the graph
const int V = 4;
// A utility function to check if the current color assignment is safe for vertex v
static bool IsSafe(int v, bool[,] graph, int[] color, int c)
{
for (int i = 0; i < V; i++)
{
if (graph[v, i] && c == color[i])
return false;
}
return true;
}
// A recursive utility function to solve m coloring problem
static bool GraphColoringUtil(bool[,] graph, int m, int[] color, int v)
{
if (v == V)
return true;
for (int c = 1; c <= m; c++)
{
if (IsSafe(v, graph, color, c))
{
color[v] = c;
if (GraphColoringUtil(graph, m, color, v + 1))
return true;
color[v] = 0;
}
}
return false;
}
// This function solves the m Coloring problem using Backtracking
static bool SolveGraphColoring(bool[,] graph, int m)
{
int[] color = new int[V];
for (int i = 0; i < V; i++)
color[i] = 0;
if (!GraphColoringUtil(graph, m, color, 0))
{
Console.WriteLine("Solution does not exist");
return false;
}
PrintSolution(color);
return true;
}
// A utility function to print solution
static void PrintSolution(int[] color)
{
Console.WriteLine("Solution Exists: Following are the assigned colors");
for (int i = 0; i < V; i++)
Console.Write(" " + color[i] + " ");
Console.WriteLine();
}
// Driver code
static void Main(string[] args)
{
/* Create following graph and test whether it is 3 colorable
(3)---(2)
| / |
| / |
| / |
(0)---(1)
*/
bool[,] graph = {
{ false, true, true, true },
{ true, false, true, false },
{ true, true, false, true },
{ true, false, true, false }
};
// Number of colors
int m = 3;
// Function call
SolveGraphColoring(graph, m);
}
}
// This code is contributed by shivamgupta310570
// Equivalent JavaScript program for M Coloring problem using backtracking
// Number of vertices in the graph
const V = 4;
// Function to print the solution
function printSolution(color) {
console.log("Solution Exists: Following are the assigned colors");
for (let i = 0; i < V; i++) {
console.log(color[i] + " ");
}
console.log("\n");
}
// Utility function to check if the current color assignment is safe for the vertex
function isSafe(v, graph, color, c) {
for (let i = 0; i < V; i++) {
if (graph[v][i] && c == color[i]) {
return false;
}
}
return true;
}
// Recursive utility function to solve the M coloring problem
function graphColoringUtil(graph, m, color, v) {
// Base case: If all vertices are assigned a color, return true
if (v === V) {
return true;
}
// Consider the vertex v and try different colors
for (let c = 1; c <= m; c++) {
// Check if assignment of color c to v is fine
if (isSafe(v, graph, color, c)) {
color[v] = c;
// Recur to assign colors to the rest of the vertices
if (graphColoringUtil(graph, m, color, v + 1)) {
return true;
}
// If assigning color c doesn't lead to a solution, remove it
color[v] = 0;
}
}
// If no color can be assigned to this vertex, return false
return false;
}
// Function to solve the M Coloring problem using backtracking
function graphColoring(graph, m) {
// Initialize all color values as 0
const color = new Array(V).fill(0);
// Call graphColoringUtil() for vertex 0
if (!graphColoringUtil(graph, m, color, 0)) {
console.log("Solution does not exist");
return false;
}
// Print the solution
printSolution(color);
return true;
}
// Driver code
const graph = [
[0, 1, 1, 1],
[1, 0, 1, 0],
[1, 1, 0, 1],
[1, 0, 1, 0],
];
const m = 3;
// Function call
graphColoring(graph, m);
// This code is contributed by shivamgupta310570
OutputSolution Exists: Following are the assigned colors
1 2 3 2
Applications of Graph Coloring:
- Design a timetable.
- Sudoku.
- Register allocation in the compiler.
- Map coloring.
- Mobile radio frequency assignment.
Related Articles:
Share your thoughts in the comments
Please Login to comment...