Graph Coloring for Competitive Programming

Graph coloring in programming refers to the assignment of colors to the vertices of a graph in a way that no two adjacent vertices share the same color. In this article, we will cover the concepts of Graph coloring, why is it important to learn for Competitive Programming and other related concepts like: Bipartite Graph, Chromatic Number, etc.

What is Graph Coloring?

Graph coloring refers to the problem of coloring vertices of a graph in such a way that no two adjacent vertices have the same color. This is also called the vertex coloring problem. If coloring is done using at most m colors, it is called m-coloring.

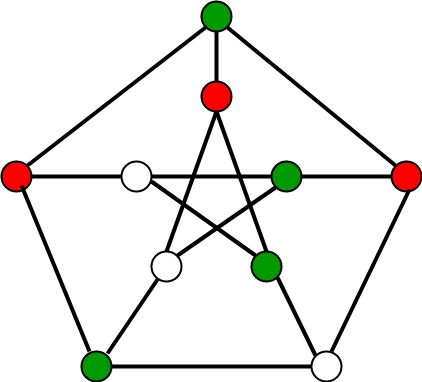
Importance of Graph Coloring in Competitive Programming(CP):

In CP as the difficulty of problems increases, the problem setter mostly chooses a graph-based problem. The solution of many such problems lies in the concept of graph coloring which mainly revolves around 3 key concepts:

• Bi-partite Coloring
• M-coloring of graph
• Chromatic Numbers

In this article, we will see how these concepts are used in a problem.

Use cases of Bipartite Graph in Competitive Programming:

A bipartite graph is a graph in which the vertices can be divided into two disjoint sets, such that no two vertices within the same set are adjacent. In other words, it is a graph in which every edge connects a vertex of one set to a vertex of the other set.

Identifying Competitive Programming Problems on Bipartite Coloring:

• When The solution Depends upon Parity of the Cycle in the graph

Imagine a problem where the solution exists only when the graph has a cycle of Even length and for Odd length cycles the solution is invalid. In these type of problem Bi-partite coloring is the easiest solution as Bipartite coloring is only possible for Even length cycles as shown in Below image:

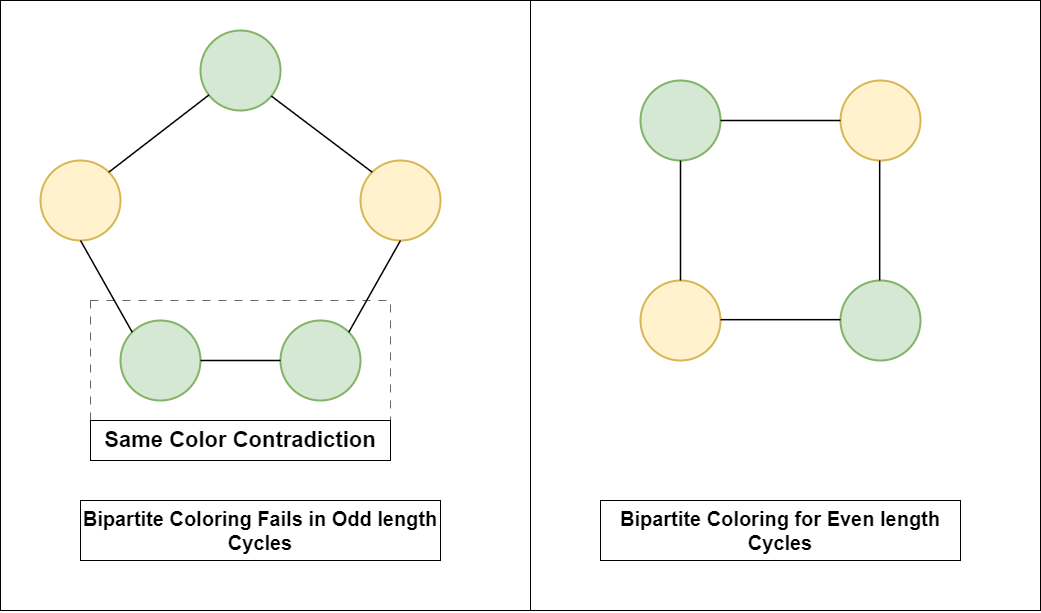
• When the solution Depends upon partitioning of graph into two subsets such that vertices in one set only have edges to the vertices of the other set

Using bipartite coloring a graph can be partitioned into two subsets such that all the vertices in the same set, does not contain any edge among them as shown in the image below:

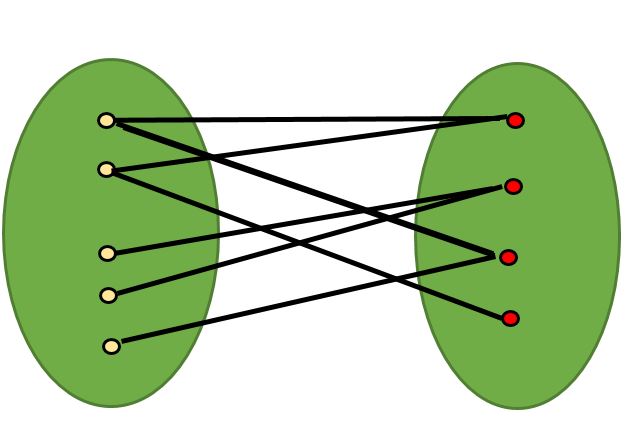
Try to Solve this problem to understand this concept properly.

Template to check if the graph is bipartite or not:

C++

// boolean variable to check if graph is bi-partite or not
bool ok;
// function taking argument: graph, color array, visited
// array, node(current node), current paint
void isBipartite(vector<vector<ll> >& g, vector<ll>& color,
                vector<ll>& vis, int node, int paint)
{
    // if current node is already painted and it is not
    // equal to requried paint return false
    if (color[node] != -1 && color[node] != paint) {
        ok = false;
        return;
    }
    // color the node to current paint
    color[node] = paint;
    if (vis[node])
        return;
    // mark the node visited
    vis[node] = 1;
    // go to each child of the node
    for (auto child : g[node]) {
        // recursive call on each adjacent child
        isBipartite(g, color, vis, child, paint xor 1);
    }
}

Java

import java.util.*;

public class GFG {

    // Boolean variable to check if the graph is bi-partite or not
    boolean ok;

    // Function to check if the graph is bi-partite
    void isBipartite(List<List<Long>> g, long[] color, boolean[] vis, int node, int paint) {
        // If the current node is already painted and it doesn't
        // match the required paint, return false
        if (color[node] != -1 && color[node] != paint) {
            ok = false;
            return;
        }

        // Color the node with the current paint
        color[node] = paint;

        // If the node is already visited, return
        if (vis[node]) {
            return;
        }

        // Mark the node as visited
        vis[node] = true;

        // Traverse each adjacent child node
        for (long child : g.get(node)) {
            // Recursive call for each adjacent child with opposite paint
            isBipartite(g, color, vis, (int) child, paint ^ 1);
        }
    }

    // Main method to execute the code
    public static void main(String[] args) {
        // Create an instance of the GFG class (or you can create a
        // new instance and call the method)
        GFG gfg = new GFG();


    }
}


// This code is contributed by shivamgupta310570

Python3

from typing import List

class GFG:
    def __init__(self):
        # Boolean variable to check if the graph is bi-partite or not
        self.ok = True

    # Function to check if the graph is bi-partite
    def is_bipartite(self, g: List[List[int]], color: List[int], vis: List[bool], node: int, paint: int):
        # If the current node is already painted and it doesn't
        # match the required paint, return false
        if color[node] != -1 and color[node] != paint:
            self.ok = False
            return

        # Color the node with the current paint
        color[node] = paint

        # If the node is already visited, return
        if vis[node]:
            return

        # Mark the node as visited
        vis[node] = True

        # Traverse each adjacent child node
        for child in g[node]:
            # Recursive call for each adjacent child with opposite paint
            self.is_bipartite(g, color, vis, child, paint ^ 1)

    # Main method to execute the code
    def main(self):
        # Create an instance of the GFG class (or you can create a
        # new instance and call the method)
        gfg = GFG()

C#

using System;
using System.Collections.Generic;

public class GFG
{
    // Boolean variable to check if the graph is bi-partite or not
    private bool ok;

    // Function to check if the graph is bi-partite
    private void IsBipartite(List<List<long>> g, long[] color, bool[] vis, int node, int paint)
    {
        // If the current node is already painted and it doesn't
        // match the required paint, return false
        if (color[node] != -1 && color[node] != paint)
        {
            ok = false;
            return;
        }

        // Color the node with the current paint
        color[node] = paint;

        // If the node is already visited, return
        if (vis[node])
        {
            return;
        }

        // Mark the node as visited
        vis[node] = true;

        // Traverse each adjacent child node
        foreach (long child in g[node])
        {
            // Recursive call for each adjacent child with opposite paint
            IsBipartite(g, color, vis, (int)child, paint ^ 1);
        }
    }

    // Main method to execute the code
    public static void Main(string[] args)
    {
        // Create an instance of the GFG class
        GFG gfg = new GFG();

        // Example usage
        int n = 4;
        List<List<long>> graph = new List<List<long>>()
        {
            new List<long>(){1, 3},
            new List<long>(){0, 2},
            new List<long>(){1, 3},
            new List<long>(){0, 2}
        };

        long[] color = new long[n];
        Array.Fill(color, -1);

        bool[] visited = new bool[n];

        gfg.ok = true;

        // Check if the graph is bi-partite
        for (int i = 0; i < n; i++)
        {
            if (!visited[i])
            {
                gfg.IsBipartite(graph, color, visited, i, 0);
            }
        }

        // Output the result
        if (gfg.ok)
        {
            Console.WriteLine("The graph is bi-partite.");
        }
        else
        {
            Console.WriteLine("The graph is not bi-partite.");
        }
    }
}

Javascript

class GFG {
    constructor() {
        // Boolean variable to check if the graph is bi-partite or not
        this.ok = true;
    }

    // Function to check if the graph is bi-partite
    isBipartite(g, color, vis, node, paint) {
        // If the current node is already painted and it doesn't
        // match the required paint, return false
        if (color[node] !== -1 && color[node] !== paint) {
            this.ok = false;
            return;
        }

        // Color the node with the current paint
        color[node] = paint;

        // If the node is already visited, return
        if (vis[node]) {
            return;
        }

        // Mark the node as visited
        vis[node] = true;

        // Traverse each adjacent child node
        for (let child of g[node]) {
            // Recursive call for each adjacent child with opposite paint
            this.isBipartite(g, color, vis, child, paint ^ 1);
        }
    }

    // Main method to execute the code
    static main() {
        // Create an instance of the GFG class (or you can create a
        // new instance and call the method)
        const gfg = new GFG();

        // Example usage:
        const adjacencyList = [
            [1, 2],
            [0, 2],
            [0, 1]
        ];

        const numNodes = 3;
        const color = new Array(numNodes).fill(-1);
        const vis = new Array(numNodes).fill(false);

        for (let i = 0; i < numNodes; i++) {
            if (!vis[i]) {
                gfg.isBipartite(adjacencyList, color, vis, i, 0);
            }
        }

        if (gfg.ok) {
            console.log("Graph is bipartite.");
        } else {
            console.log("Graph is not bipartite.");
        }
    }
}

// Call the main method
GFG.main();

Time Complexity: O(V+E) where V is the number of edges and E is the number of Edges in the graph.

M-coloring and Chromatic Numbers in Graph Coloring:

The “M-coloring” of a graph refers to the assignment of colors to the vertices of a graph such that no two adjacent vertices share the same color. The chromatic number of a graph is the minimum number of colors needed to color the vertices of the graph in such a way that no two adjacent vertices have the same color.

Use cases in Competitive Programming:

• Map Coloring Problem: In this problem vertices of the graph represents a state/country while the edges represent the border between those countries. The aim of this problem is to provide distinguish attributes to the neighboring states by providing distinguish colors.
• Scheduling Problems: Representing tasks as vertices and dependencies between tasks as edges, the goal is to schedule the tasks in such a way that no two dependent tasks are scheduled at the same time.
• Graph Partitioning: Graph coloring is used in partitioning a graph into different sets or components. This can be applied in problems where we need to calculate the different ways of resource distribution.
• Job Scheduling Problems: Representing jobs as vertices and dependencies as edges, the goal is to maximize the throughput by best resource allocation.
• Four-Color Theorem: Every planar graph can be colored with at most four colors. This concept can be used in advanced problems where the answer depends upon the four coloring of a planar graph.

Practice Problems on Graph Coloring for Competitive Programming:

Article Link	Problem Link
M-Coloring Problem	Solve Now
Maximum Bipartite Matching	Solve Now
Minimum labelled node to be removed from undirected Graph such that there is no cycle	Solve Now
Find two disjoint good sets of vertices in a given graph	Solve Now
Minimum steps to color the tree with given colors	Solve Now
Edge Coloring of a Graph	Solve Now
Coloring a Cycle Graph	Solve Now
Check whether a given graph is Bipartite or not	Solve Now
Minimum number of days required to schedule all exams	Solve Now
Minimize colors to paint graph such that no path have same color	Solve Now