Chinese Postman or Route Inspection | Set 1 (introduction)
Last Updated :
07 Jul, 2022
Chinese Postman Problem is a variation of Eulerian circuit problem for undirected graphs. An Euler Circuit is a closed walk that covers every edge once starting and ending position is same. Chinese Postman problem is defined for connected and undirected graph. The problem is to find shortest path or circuity that visits every edge of the graph at least once.
If input graph contains Euler Circuit, then a solution of the problem is Euler Circuit
An undirected and connected graph has Eulerian cycle if “all vertices have even degree“.
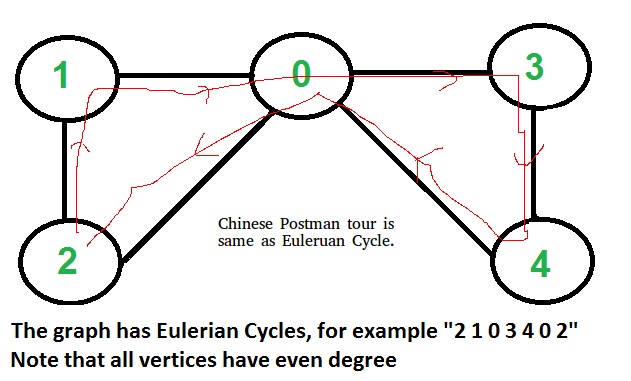
It doesn’t matter whether graph is weighted or unweighted, the Chinese Postman Route is always same as Eulerian Circuit if it exists. In weighted graph the minimum possible weight of Postman tour is sum of all edge weights which we get through Eulerian Circuit. We can’t get a shorter route as we must visit all edges at-least once.
If input graph does NOT contain Euler Circuit
In this case, the task reduces to following.
1) In unweighted graph, minimum number of edges to duplicate so that the given graph converts to a graph with Eulerian Cycle.
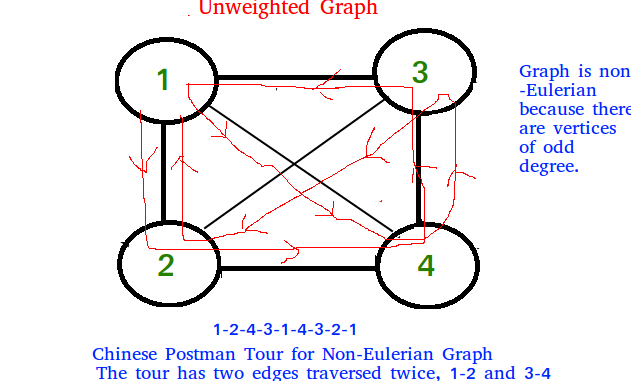
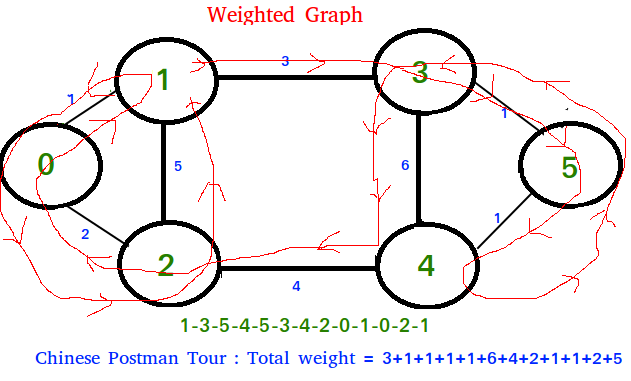
2) In weighted graph, minimum total weight of edges to duplicate so that given graph converts to a graph with Eulerian Cycle.
Algorithm to find shortest closed path or optimal
Chinese postman route in a weighted graph that may
not be Eulerian.
step 1 : If graph is Eulerian, return sum of all
edge weights.Else do following steps.
step 2 : We find all the vertices with odd degree
step 3 : List all possible pairings of odd vertices
For n odd vertices total number of pairings
possible are, (n-1) * (n-3) * (n -5)... * 1
step 4 : For each set of pairings, find the shortest
path connecting them.
step 5 : Find the pairing with minimum shortest path
connecting pairs.
step 6 : Modify the graph by adding all the edges that
have been found in step 5.
step 7 : Weight of Chinese Postman Tour is sum of all
edges in the modified graph.
step 8 : Print Euler Circuit of the modified graph.
This Euler Circuit is Chinese Postman Tour.
Illustration :
3
(a)-----------------(b)
1 / | | \1
/ | | \
(c) | 5 6| (d)
\ | | /
2 \ | 4 | /1
(e)------------------(f)
As we see above graph does not contain Eulerian circuit
because is has odd degree vertices [a, b, e, f]
they all are odd degree vertices .
First we make all possible pairs of odd degree vertices
[ae, bf], [ab, ef], [af, eb]
so pairs with min sum of weight are [ae, bf] :
ae = (ac + ce = 3 ), bf = ( bd + df = 2 )
Total : 5
We add edges ac, ce, bd and df to the original graph and
create a modified graph.
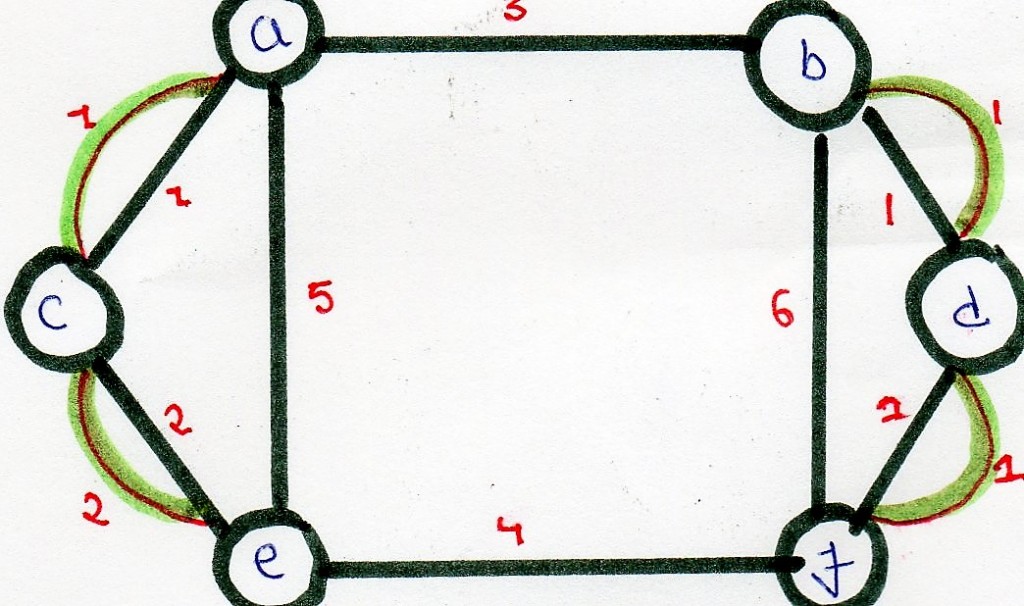
Optimal chinese postman route is of length : 5 + 23 =
28 [ 23 = sum of all edges of modified graph ]
Chinese Postman Route :
a - b - d - f - d - b - f - e - c - a - c - e - a
This route is Euler Circuit of the modified graph.
Share your thoughts in the comments
Please Login to comment...