Erdos Renyl Model (for generating Random Graphs)

In graph theory, the Erdos–Rényi model is either of two closely related models for generating random graphs. 

There are two closely related variants of the Erdos–Rényi (ER) random graph model. 

In the G(n, M) model, a graph is chosen uniformly at random from the collection of all graphs which have n nodes and M edges. For example, in the G(3, 2) model, each of the three possible graphs on three vertices and two edges are included with probability 1/3. 

In the G(n, p) model, a graph is constructed by connecting nodes randomly. Each edge is included in the graph with probability p independent from every other edge. Equivalently, all graphs with n nodes and M edges have equal probability of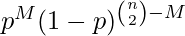 

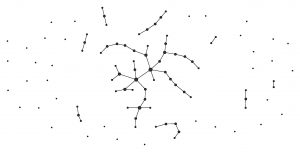
 A graph generated by the binomial model of Erdos and Rényi (p = 0.01) 

The parameter p in this model can be thought of as a weighting function; as p increases from 0 to 1, the model becomes more and more likely to include graphs with more edges and less and less likely to include graphs with fewer edges. In particular, the case p = 0.5 corresponds to the case where all 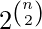graphs on n vertices are chosen with equal probability. 

The article will basically deal with the G (n,p) model where n is the no of nodes to be created and p defines the probability of joining of each node to the other. 

Properties of G(n, p)

With the notation above, a graph in G(n, p) has on average 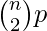edges. The distribution of the degree of any particular vertex is binomial:

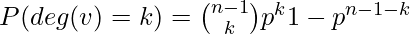
Where n is the total number of vertices in the graph. 

Since 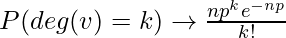as 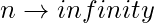and np= constant This distribution is Poisson for large n and np = const. In a 1960 paper, Erdos and Rényi described the behaviour of G(n, p) very precisely for various values of p. Their results included that:

• If np < 1, then a graph in G(n, p) will almost surely have no connected components of size larger than O(log(n)).
• If np = 1, then a graph in G(n, p) will almost surely have a largest component whose size is of order .
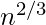• If np 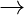c > 1, where c is a constant, then a graph in G(n, p) will almost surely have a unique giant component containing a positive fraction of the vertices. No other component will contain more than O(log(n)) vertices.
• If 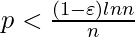, then a graph in G(n, p) will almost surely contain isolated vertices, and thus be disconnected.
• If 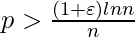, then a graph in G(n, p) will almost surely be connected.

Thus 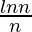is a sharp threshold for the connectedness of G(n, p). Further properties of the graph can be described almost precisely as n tends to infinity. For example, there is a k(n) (approximately equal to 2log2(n)) such that the largest clique in G(n, 0.5) has almost surely either size k(n) or k(n) + 1. Thus, even though finding the size of the largest clique in a graph is NP-complete, the size of the largest clique in a “typical” graph (according to this model) is very well understood. Interestingly, edge-dual graphs of Erdos-Renyi graphs are graphs with nearly the same degree distribution, but with degree correlations and a significantly higher clustering coefficient. 

Next I’ll describe the code to be used for making the ER graph. For implementation of the code below, you’ll need to install the netwrokx library as well you’ll need to install the matplotlib library. Following you’ll see the exact code of the graph which has been used as a function of the networkx library lately in this article. 

Erdos_renyi_graph(n, p, seed=None, directed=False)

Returns a G(n,p) random graph, also known as an Erdos-Rényi graph or a binomial graph. 
The G(n,p) model chooses each of the possible edges with probability p. The functions binomial_graph() and erdos_renyi_graph() are aliases of this function. 

Parameters: n (int) – The number of nodes. 
p (float) – Probability for edge creation. 
seed (int, optional) – Seed for random number generator (default=None). 
directed (bool, optional (default=False)) – If True, this function returns a directed graph.

Python

#importing the networkx library
>>> import networkx as nx

#importing the matplotlib library for plotting the graph
>>> import matplotlib.pyplot as plt

>>> G= nx.erdos_renyi_graph(50,0.5)
>>> nx.draw(G, with_labels=True)
>>> plt.show()

Figure 1: For n=50, p=0.5

The above example is for 50 nodes and is thus a bit unclear. 

When considering the case for lesser no of nodes (for example 10), you can clearly see the difference. 

Using the codes for various probabilities, we can see the difference easily: 

Python

>>>H= nx.erdos_renyi_graph(10,0.5)
>>> nx.draw(H, with_labels=True)
>>> plt.show()

Figure 2: For n=10, p=0

Python

>>> K=nx.erdos_renyi_graph(10,0.25)
>>> nx.draw(K, with_labels=True)
>>> plt.show()

Figure 3: For n=10, p=0.25

Python

>>>H= nx.erdos_renyi_graph(10,0.5)
>>> nx.draw(H, with_labels=True)
>>> plt.show()

Figure 4: For n=10, p=0.5

This algorithm runs in O(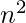) time. For sparse graphs (that is, for small values of p), fast_gnp_random_graph() is a faster algorithm. Thus the above examples clearly define the use of erdos renyi model to make random graphs and how to use the foresaid using the networkx library of python. Next we will discuss the ego graph and various other types of graphs in python using the library networkx. 

.