Division in maths is a way of sharing or grouping numbers into equal parts. It helps us understand how many times one number can fit into another. It is a mathematical operation that involves splitting something into equal parts. It is also one of the four basic arithmetic operations, along with addition, subtraction, and multiplication.
Division is the mathematical operation opposite to multiplication. It involves distributing a number into equal portions or sets. When we perform division, we decompose a larger number into smaller units, ensuring that they reconstruct the original number when these units are multiplied together. For instance, dividing 4 by 2 yields 2, because splitting 4 into 2 equal parts results in each part being 2.
In this article, we will learn the division method, its symbol, examples, how to perform division, properties, and applications in detail.
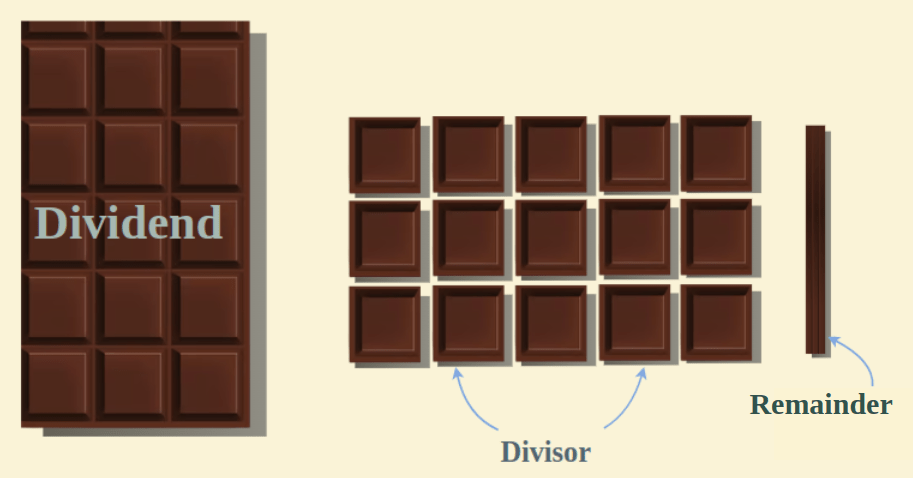
What is Division in Maths?
The division operation in mathematics is used for finding the smaller group into which a large group of numbers. It is used to the larger group into smaller groups.
Suppose we have 32 chapatis and 8 children to feed then one child gets how many chapatis is found out using division operation as,
32/8 = 4
Thus, each child gets four chapatis, the divisions in maths is very useful for finding the smaller groups of the number and for simplifying the arithmetic problems. Also, It holds significance for class 2 divide as well.
Division Meaning
Division in Maths is defined as the method of repetitive subtraction. The division is also called the opposite method of multiplication.
Suppose we have to find the division of 16 by 4 then 4 is subtracted from 16 four times, 16 – 4 – 4 – 4 – 4 = 0. Thus, the dividing maths is referred to as repetitive subtraction and 16/4 = 4.
Division by Zero
Dividing any number by zero lacks divisional meaning, yielding a result expressed as infinity. For instance, 14/0 = ∞, signifying undefined.
Division Symbol
The symbol used to denote the division is ÷ (obelus) and / (backslash). These symbols are used for division, suppose we have to divide 24 by 6 then this is represented as,
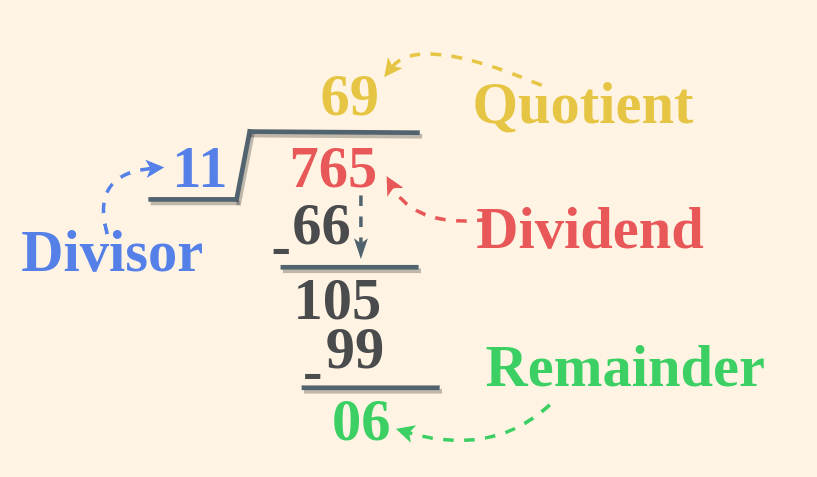
Parts of Division
There are four parts to the division that includes,
- Dividend
- Divisor
- Quotient
- Remainder
|
Parts of Division Process
|
|
Terms
|
Description
|
Example
|
|
Dividend
|
The number that is to be divided is called the Dividend.
|
52
|
|
Divisor
|
The value of the portion which is taken out is called the Divisor
|
6
|
|
Quotient
|
The number of equal portions in which the dividend is divided is called the Quotient.
|
8
|
|
Remainder
|
The remaining value left is called the remainder.
|
4
|
The equation or the technique used to find the division of the number is called the division formula sometimes also known as division algorithm.
The division algorithm or the division in math formula is,
Dividend = (Divisor × Quotient) + Remainder
This algorithm is used to verify the results of the division process, the division of two numbers yields a quotient and the remainder which when used verified the results of the division.
This can be understood using the following example of division,
Example: Divide math 22 by 3.
22 divided by 3 will give us 7 as the quotient and 1 as the remainder.
Dividend = (Divisor × Quotient) + Remainder
22 = (3 × 7) + 1
22 = 21 + 1
22 = 22
Hence verified.
How To Do Division – Rule
The division of one digit number can be directly performed using the tables of various numbers, such as suppose we have to find the division of 24 by 4 then we know that by the table of 4,
4×6 = 24, thus
24/4 = 6
For two-digit or three-digit numbers division is performed using the steps discussed below, here we use the example of division, 77 divided by 4 to get the steps of division.
Step-by-Step Guide to Division
Here is a stepwise method of doing division in maths.
Step 1: Using the symbol ⟌ write the divisor (here 4) on its left side and the dividend (here 77) enclosed under the division symbol(⟌).

Step 2: Starting from the left-hand side take one digit of the dividend at a time and check whether it is smaller or greater than the divisor. If the digit is smaller then take two digits at a time. (here, 7 is greater than 4).
Step 3: Take the multiple of the divisor that is equal to or less than the digits in step 2. (here 4×1 = 4, i.e. less than 7). Write the number in the Quotient.
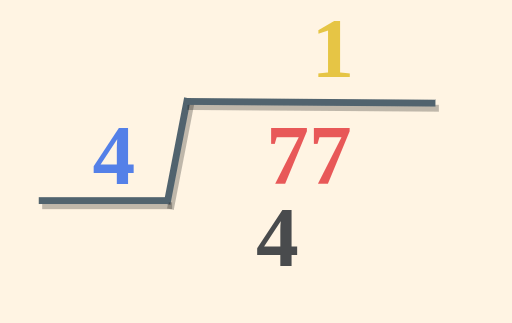
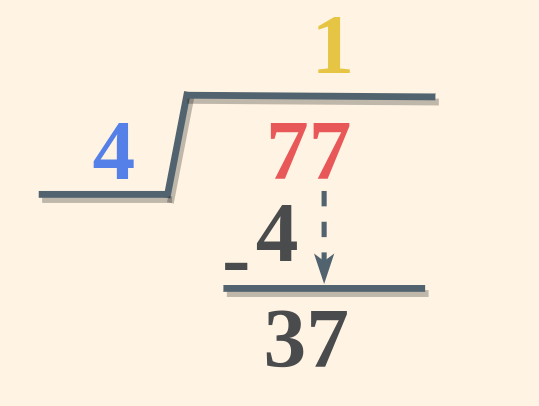
Step 4: Subtract the multiple of the divisor from the digits in Step 2 and write the remainder and then carry the next digit from the dividend.
If the number is less than the divisor add zero in the quotient and bring the next digit down, repeat this process till the divisor is greater than the number. (here 7 – 4 = 3)
Step 5: Now again find the suitable multiple of the quotient and repeat the above process till the remainder so obtained is less than the divisor.
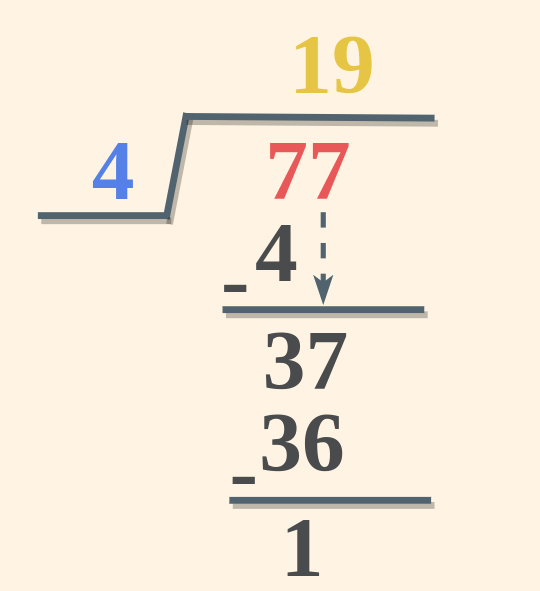
Step 6: When the remainder obtained is less than the divisor the Quotient and the remainder so obtained are the result of the division.
Division with Remainders
The number left at the end of the division process is called the remainder of the division and it is not always zero. But it is always less than the divisor. This can be understood by the example discussed below,
Example: 14 ÷ 2
- Quotient = 7
- Remainder = 0
Example: 15 ÷ 2
- Quotient = 7
- Remainder = 1
Division of Fractions
Fractions can also be easily divided and the divisibility rules for dividing the fractions are different from dividing natural numbers. If we in math divide a fraction from another fraction then the latter is multiplied with the former by taking its reciprocal.
This can be understood as,
a/b ÷ c/d = a/b × d/c
For example, Divide 2/5 by 4/3
= (2/5) ÷ (4/3)
Now, converting “÷” into “×” and taking the reciprocal of the divisor
(2/5) × (3/4)
= 6/20
= 3/10
Thus, the division 2/5 by 4/3 gives 3/10
Division Properties
Some of the most important + properties of the math division operation are,
Property of Division by 1: If we divide any number by 1 then the quotient is the number itself. This can be understood by the example, 23 divided by 1 then the result is 23, thus,
If Divisor = 1, then Dividend = Quotient
Property of Division by 0: If we divide maths any number by 0 then the quotient is undefined as the division of zero is not possible. This can be understood by the example, 23 divided by 0 then the result is undefined, thus,
If Divisor = 0, then Quotient = Undefined (Division is not possible), i.e.
n/0 = Undefined, for any number n (n ≠ 0)
Property of Division by Itself: If we divide any number by itself then the quotient is the 1. This can be understood by the example, 23 divided by 23 then the result is 1, thus,
If Divisor = Dividend then, Quotient = 1
Property of Division of 0 by Any Number: If we divide the sums any number by 0 then the quotient is always 0. This can be understood by the example, 0 divided by 23 then the result is 0, thus,
If Dividend = 0 for any Divisor, Quotient = 0
Property of Division by 10: If we divide any number by 10 then the quotient is the number itself without the one’s digit and the remainder is one’s digit. This can be understood by the example, 237 divided by 10 then the result is 23, and 7 is the remainder, thus,
If Divisor = 10, then Quotient = Dividend without the One’s Digit and Remainder = One’s Digit
Property of Division by a Power of 10: If we divide any number by the Power of 10 then the quotient is the number obtained by removing the digits (from the right-hand side) from the number as there are a number of zeroes or exponent in the divisor. This can be understood by the example, 2376 divided by 100 now here there are two zeroes in the divisor then the result is 23, and 76 is the remainder, thus,
If Divisor = 10n, then Quotient = Dividend without the n digit from last and Remainder = Last n digits of the number.
Division of 2 Digit Number
In division 2 digits we study how to divide a two digit number by one digit number. The same can be studied by the examples added below,
Example: Divide 96 by 4
Using Division Algorithm,
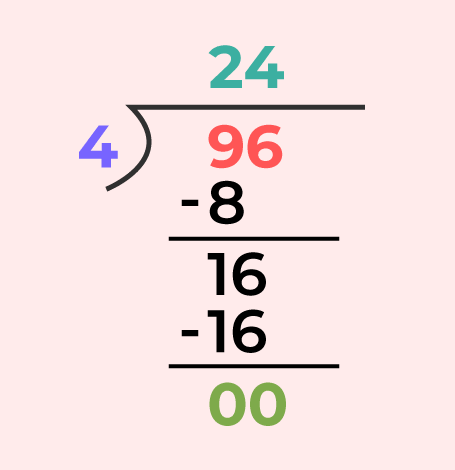
- Quotient = 24
- Remainder = 0
Example: Divide 56 by 5.
Using Division Algorithm
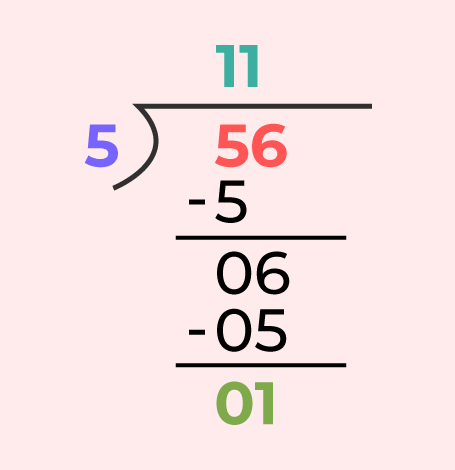
- Quotient = 11
- Remainder = 1
Division of 3 Digit Number
In division 3 digits we study how to divide a three digit number by one digit number. The same can be studied by the examples added below,
Example: Divide 196 by 6
Using Division Algorithm
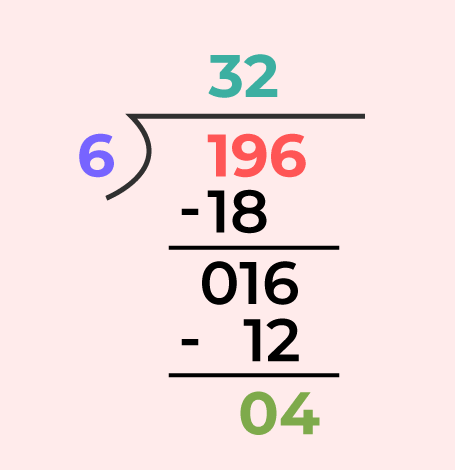
- Quotient = 32
- Remainder = 4
Example: Divide 546 by 5
Using Division Algorithm
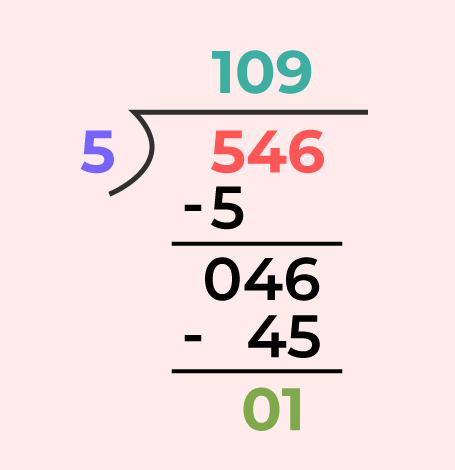
- Quotient = 129
- Remainder = 1
Division Sum
Division sum contains the sums or the problems related to the division. Some example problems of division sums are,
Division Sum Problem 1. If we have to distribute 20 mangoes among 5 boys then each boys gets how many mangoes?
Solution:
Total mangoes = 20
Number of boys = 5
Each boy gets mangoes = 20/5
= 4 mangoes
Thus, each boys gets 4 mangoes.
Division Sum Problem 2. Krisha has 45 sweets to distribute in his class if there are 15 students in his class then how many sweets each student of the class gets?
Solution:
Total sweets = 45
Number of students in class = 15
Each student gets sweets = 45/15
= 3 sweets
Thus, each boys gets 3 sweets.
Long Division in Maths
Long division is a method of dividing one number (the dividend) by another number (the divisor) to find the quotient (the result) and, optionally, the remainder.
It is called “long division” because it often involves writing out the division problem with multiple steps and carrying out the division process one digit at a time, working from left to right.
Division Tricks and Divisibility Check
If a number can be divided by a single-digit number without any remainder, it is considered divisible. There are quick methods to determine divisibility without performing the actual division.
Some of the most important tricks of the math division operation, including divisibility, shortcuts of division, and tricks of division, are:
- Divisible by 2: If a number is even, meaning it ends in 0, 2, 4, 6, or 8. Example: 746 is divisible by 2.
- Divisible by 3: Sum of its digits is a multiple of 3. Example: 471 is divisible by 3 because 4 + 7 + 1 = 12, and 1 + 2 = 3.
- Divisible by 4: Last two digits form a multiple of 4. Example: 7,324 is divisible by 4 because 24 is a multiple of 4.
- Divisible by 5: Last digit is 0 or 5. Example: 285 is divisible by 5.
- Divisible by 6: Divisible by both 2 and 3. Example: 438 is divisible by 6 because it is even, and the digit sum is a multiple of 3.
- Divisible by 8: Last three digits form a multiple of 8. Example: 42,976 is divisible by 8 because 976 is a multiple of 8.
- Divisible by 9: Sum of its digits is a multiple of 9. Example: 7,281 is divisible by 9 because 7 + 2 + 8 + 1 = 18, and 1 + 8 = 9.
- Divisible by 10: Last digit is 0. Example: 91,420 is divisible by 10.
Division Solved Examples
Here are some solved examples on Division for you help.
Example 1: Divide 45 by 6 and verify using Division Algorithm.
Solution:
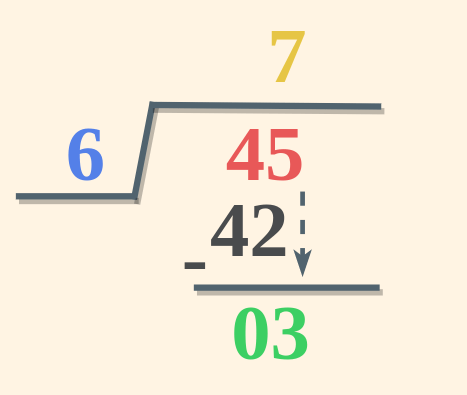
- Dividend = 45
- Divisor = 6
- Quotient = 7
- Remainder = 3
Division Algorithm
Dividend = (Divisor × Quotient) + Remainder
45 = 6 × 7 + 3
45 = 42 + 3
45 = 45
Hence verified.
Example 2: Divide 145 by 9 and verify using Division Algorithm.
Solution:
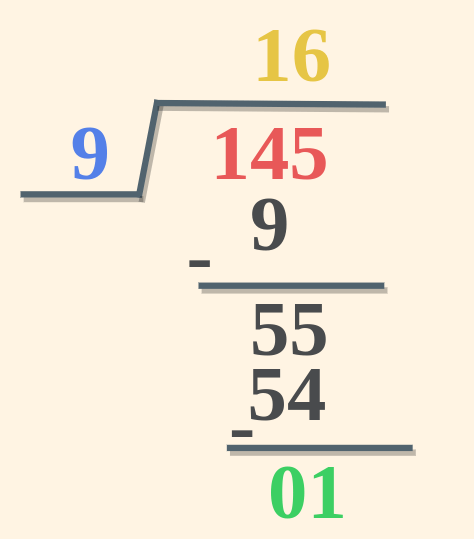
- Dividend = 145
- Divisor = 9
- Quotient = 16
- Remainder = 1
Division Algorithm
Dividend = (Divisor × Quotient) + Remainder
145 = 9 × 16 + 1
145 = 144 + 1
145 = 145
Hence verified.
Example 3: Divide 48 by 4 and verify using Division Algorithm.
Solution:
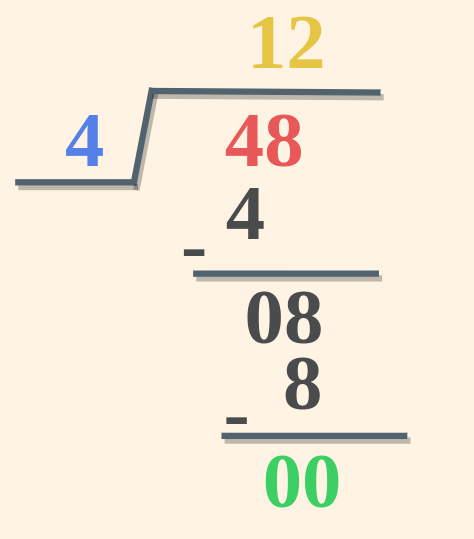
- Dividend = 48
- Divisor = 4
- Quotient = 12
- Remainder = 0
Division Algorithm
Dividend = (Divisor × Quotient) + Remainder
48 = 4 × 12 + 0
48 = 48 + 0
48 = 48
Hence verified.
Division Worksheet Class 2 and 3
Here are some practice problems on Division in Maths for you to solve.
Problem 1. If we divide 25 pencils among 5 students. How many pencils will each student receive?
Problem 2. If a farmer has has harvested 368 apples, and he distributes them in 4 baskets. How many apples will be in each basket?
Problem 3. A bakery bakes 72 breads and needs to distribute it among 12 different persons. How many bread each person gets?
Problem 4. In a garden there are 45 different flowers equally distributed in 5 rows then each row has how many flowers?
Summary – Division in Maths
In conclusion, division is a fundamental mathematical operation that serves as the inverse of multiplication, playing a critical role in both education and daily life. Through the act of dividing, we distribute a larger quantity into smaller, equal parts, allowing for the systematic breakdown and analysis of problems. Whether applied in simple arithmetic to determine equal sharing, or in more complex scenarios involving fractions, decimals, or percentages, division helps us understand patterns, manage resources, and make informed decisions. Its practical applications, from budgeting in personal finances to calculating per-unit costs in business, highlight its importance in fostering mathematical literacy and problem-solving skills. Embracing the concept of division equips individuals with the ability to navigate the myriad quantitative challenges encountered in the real world.
FAQs on Division In Maths
What is Division in Maths?
Division in mathematics is one of the four fundamental operations of mathematics that include, Addition, Subtraction, Multiplication, and Division. The meaning of division is the repetitive process of subtraction. It holds significance for Division for Class 2 as well.
What are the parts of Division?
The parts of the division are:
- Dividend
- Divisor
- Quotient
- Remainder
What is the Division Symbol?
Division symbol in maths is called obelus which is represented by ÷. Sometimes a backslash written as ‘/’ is also used to represent division in mathematical equations.
What is the Division Algorithm Formula?
Division Algorithm Formula is: Dividend = (Divisor × Quotient) + Remainder
What are types of Division?
There are Two Types of Division that are,
- Partitive Division: Dividing a number into a known amount of groups.
- Quotative Division: Dividing a number into a specific quantity.
What is the remainder formula?
Remainder formula is as follows, Remainder = Dividend – (Divisor × Quotient)
What is the value of a number when divided by 0?
When dividing any number by 0, the result is infinity, making the division by 0 undefined.
Share your thoughts in the comments
Please Login to comment...