Definite Integral as the Limit of a Riemann Sum
Last Updated :
16 Jun, 2021
Definite integrals are an important part of calculus. They are used to calculate the areas, volumes, etc of arbitrary shapes for which formulas are not defined. Analytically they are just indefinite integrals with limits on top of them, but graphically they represent the area under the curve. The limits denote the boundaries between which the area should be calculated. These concepts hold a lot of importance in the field of electrical engineering, robotics, etc. For defining integrals, Riemann sums are used in which we calculate the area under any curve using infinitesimally small rectangles. Let’s look at this interpretation of definite integrals in detail.
Riemann Sums
Riemann’s sums and integrals were developed by German mathematician Bernhard Riemann who made significant contributions to the field of differential geometry, number theory, and its analysis. These sums calculate the area under any curve using infinite rectangles and summing up their area. Let’s understand these sums through an example, consider a function f(x), the objective is to calculate the area under this curve between x = a to x = b.

In the definite integral notation, this area will be represented as,
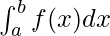
This area can be approximated by dividing the area under the curve into n equally sized rectangles. So, the interval [a, b] is divided into n-subintervals defined by the points.

a = x0 < x1 < x2 < …. xn-2< xn-1 < xn = b
Then, the n intervals are,
[x0, x1], [x1, x2], …. [xn-1, xn]
So, for the ith rectangle, the width will be, [xi-1, xi].
The area for ith rectangle Ai = f(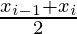 )(xi — xi-1)
)(xi — xi-1)
So, the total area will be 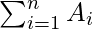
This sum is called Riemann sum.
Definite Integrals through Riemann Sums
Through Riemann sums, the area under the curve can be calculated for arbitrarily complex functions. So, definite integrals can be defined using the Riemann sums. Intuitively, as we increase the number of rectangles in the region, their width decreases and the area becomes close and close to the exact area under the curve.

Let P be the width of the largest interval.
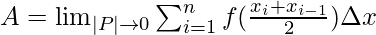
This limit is the definite integral of the function f(x) between the limits a to b and is denoted by 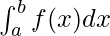 . Let n be the number of divisions we make in the limits and R(n) be the value of riemann sum with n-divisions as n ⇢ ∞, R(n) becomes closer and closer to the actual area. Let’s see some problems on these concepts.
. Let n be the number of divisions we make in the limits and R(n) be the value of riemann sum with n-divisions as n ⇢ ∞, R(n) becomes closer and closer to the actual area. Let’s see some problems on these concepts.
Sample Problems
Question 1: Find the value of riemann sum for n = 3 for the function f(x) = 5 between x = 0 to x = 6.
Solution:
Dividing the interval into four equal parts that is n = 3. The width of each interval will be,
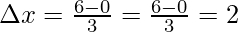
The value of the function in each interval will be the value of the function at the mid-point of the interval.
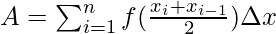
⇒A = 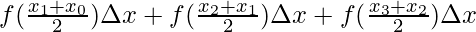
⇒A = 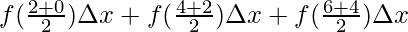
⇒A = 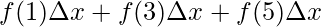
⇒A = 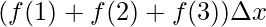
⇒A = (5 + 5 + 5)2
⇒A = 30
Question 2: Find the value of riemann sum for n = 4 for the function f(x) = 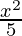 between x = 0 to x = 4.
between x = 0 to x = 4.
Solution:
Dividing the interval into four equal parts that is n = 4. The width of each interval will be,
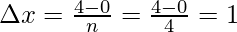
The value of the function in each interval will be the value of the function at the mid-point of the interval.
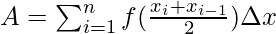
⇒A = 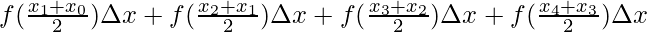
⇒A = 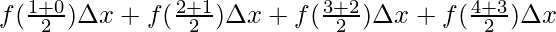
⇒A = 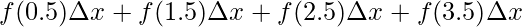
⇒A = 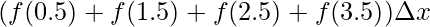
⇒A = 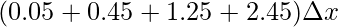
⇒A = 4.2
Question 3: Find the value of riemann sum for n = 6 for the function f(x) = x between x = 0 to x = 6.
Solution:
Dividing the interval into four equal parts that is n = 6. The width of each interval will be,
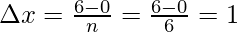
The value of the function in each interval will be the value of the function at the mid-point of the interval.
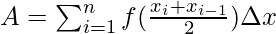
⇒A = 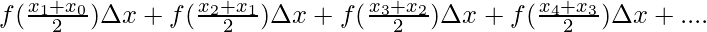
⇒A = 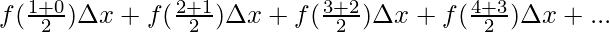
⇒A = 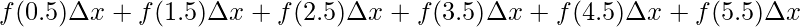
⇒A = + 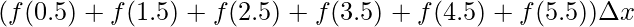
⇒A = 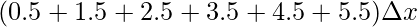
⇒A = 18
Question 4: Find the value of definite integral f(x) = 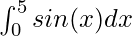
Solution:
f(x) = 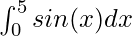
⇒f(x) = ![Rendered by QuickLaTeX.com [-cos(x)]^{5}_{0}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-1aa0ddbc6c6452b20359d8376f3a884e_l3.png)
⇒f(x) = ![Rendered by QuickLaTeX.com [cos(x)]^{0}_{5}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-a1d557c5c6204b6d0492fc6110b9b08a_l3.png)
⇒f(x) = 1 – cos(5)
Question 5: Find the value of definite integral f(x) = 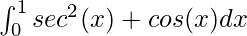
Solution:
f(x) = 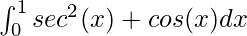
⇒f(x) = 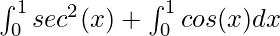
⇒f(x) = ![Rendered by QuickLaTeX.com [tan(x)]^{1}_{0} + [sin(x)]^1_0](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-35395b6a20da96f897491e180eea5635_l3.png)
⇒f(x) = tan(1) – tan(0) + sin(1) – sin(0)
⇒f(x) = tan(1) + sin(1)
Question 6: Find the value of riemann sum for n = 3 for the function f(x) = log(x) between x = 1 to x = 4.
Solution:
Dividing the interval into four equal parts that is n = 3. The width of each interval will be,
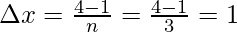
The value of the function in each interval will be the value of the function at the mid-point of the interval.
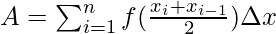
⇒A = 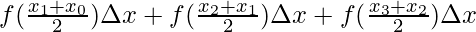
⇒A = 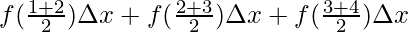
⇒A = 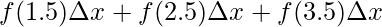
⇒A = 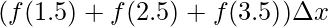
⇒A = 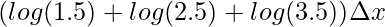
⇒A = (0.17 + 0.39 + 0.54)
⇒A = 0.56 + 0.54
⇒A = 1.1
Question 7: Find the value of riemann sum for n = 2 for the function f(x) = ex between x = 0 to x = 4.
Solution:
Dividing the interval into four equal parts that is n = 2. The width of each interval will be,
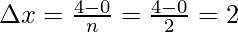
The value of the function in each interval will be the value of the function at the mid-point of the interval.
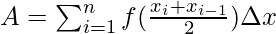
⇒A = 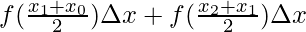
⇒A = 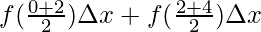
⇒A = 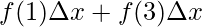
⇒A = 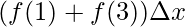
⇒A = 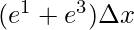
⇒A = (2.7 + 20)2
⇒A = (22.7)(2)
⇒A = 45.4
Share your thoughts in the comments
Please Login to comment...