Data Structures and Algorithms | Set 35
Last Updated :
14 Dec, 2022
Following questions have been asked in GATE CS 2014 exam.
1) The number of distinct minimum spanning trees for the weighted graph below is ____
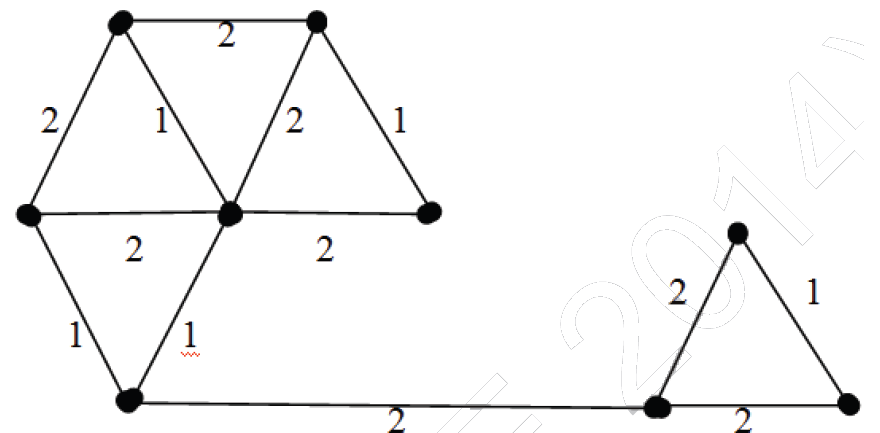
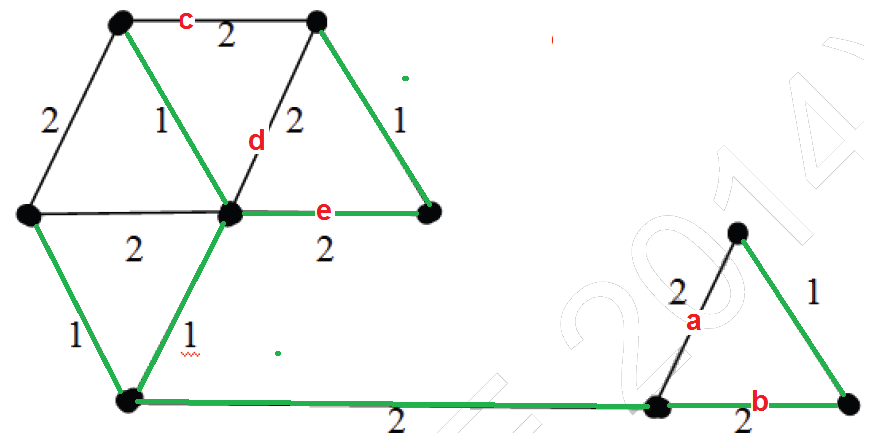
Answer: 6
Highlighted (in green) are the edges picked to make a MST. In the right side of MST, we could either pick edge ‘a’ or ‘b’. In the left side, we could either pick ‘c’ or ‘d’ or ‘e’ in MST.
There are 2 options for one edge to be picked and 3 options for another edge to be picked. Therefore, total 2*3 possible MSTs.
2) Consider the following rooted tree with the vertex P labeled as root
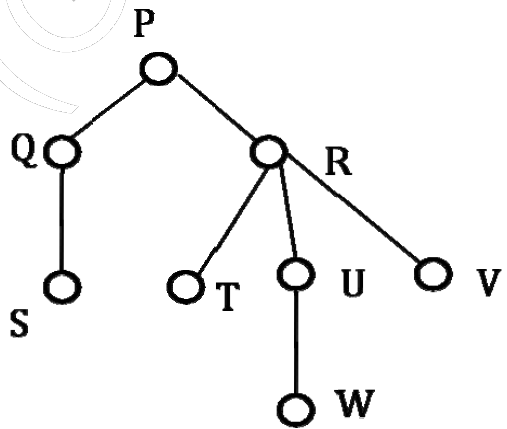
The order in which the nodes are visited during in-order traversal is
(A) SQPTRWUV
(B) SQPTURWV
(C) SQPTWUVR
(D) SQPTRUWV
Answer: (A)
The only confusion in this question is, there are 3 children of R. So when should R appear – after U or after R? There are two possibilities: SQPTRWUV and SQPTWURV. Only 1st possibility is present as an option A, the IInd possibility is not there. Therefore option A is the right answer.
3) Let A be a square matrix of size n x n. Consider the following program. What is the expected output?
C = 100
for i = 1 to n do
for j = 1 to n do
{
Temp = A[i][j] + C
A[i][j] = A[j][i]
A[j][i] = Temp - C
}
for i = 1 to n do
for j = 1 to n do
Output(A[i][j]);
|
(A) The matrix A itself
(B) Transpose of matrix A
(C) Adding 100 to the upper diagonal elements and subtracting 100 from diagonal elements of A
(D) None of the above
Answer: A
If we take look at the inner statements of first loops, we can notice that the statements swap A[i][j] and A[j][i] for all i and j.
Since the loop runs for all elements, every element A[l][m] would be swapped twice, once for i = l and j = m and then for i = m and j = l. Swapping twice means the matrix doesn’t change.
4) The minimum number of arithmetic operations required to evaluate the polynomial P(X) = X5 + 4X3 + 6X + 5 for a given value of X using only one temporary variable.
(A) 6
(B) 7
(C) 8
(D) 9
Answer: B
We can parenthesize the polynomial to minimize the number of operations (See Horner’s Method). We get X(X2(X2 + 4) + 6) + 5 after parenthesization.
Following is sequence of operations to be used.
Note that we are allowed to use only one variable.
res = X*X
res = res + 4
res = X*res
res = X*res
res = res + 6
res = X*res
res = res + 5
5) You have an array of n elements. Suppose you implement quicksort by always choosing the central element of the array as the pivot. Then the tightest upper bound for the worst case performance is
(A) O(n2)
(B) O(nLogn)
(C) Θ(nLogn)
(D) O(n3)
Answer: (A)
The middle element may always be an extreme element (minimum or maximum) in sorted order, therefore time complexity in worst case becomes O(n2)
See GATE Corner for all previous year paper/solutions/explanations, Syllabus, Important dates, Notes, etc.
Share your thoughts in the comments
Please Login to comment...